搜索引擎算法之初探——PageRank、DocRank

从文档集合中找出出现搜索词的文档，进一步可能是通过搜索词在文档中出现的次数来对文档排名，这种搜索就是信息检索（Information retrieval）。

有很多现有的库可以很方便的就让我们做出来这些工作，其中最有名的当属Lucene了。当然，现在的搜索已不单单是索引了，而在于链接分析、用户点击分析和自然语言处理等方面，这些技术能大大的增强搜索的性能。

基本搜索

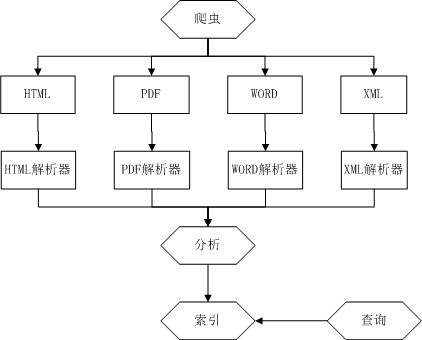
构建一个搜索引擎的基本步骤应该有五步：爬取、解析、分析、索引、搜索。如下图所示：

爬取用以获得所需要的文档数据；解析将这些数据转化为统一的结构；分析是对数据进行分词，去除不重要的词语；索引步骤先将文档分为不同的实体：邮件、记录、新闻等，每个实体中分为不同的域，比如（title/content等），然后将title部分放到索引文件中，将content放到其他文件中，然后对content建立查询索引，方便查询，（注意：该步骤建立了两个索引，一个索引中包含有文档正文外的部分title、url等，一个索引是对文档content进行索引，方便获取出现某查询串的所有文档）；查询时是对文档的content索引进行查询，找到包含查询串的所有文档，然后从索引文件中获取title，这个索引的作用就是一个指向content的指针，每次查询都向用户展示文档的title，用户点击title才能得到整个文档。

PageRank

搜索的整个流程便介绍完了，我们下面所讲的PageRank等算法，还有第一段提到的按照出现次数排序都是对查询结果进行排序，即搜索引擎排名算法。

传统的通过词频什么的进行排名的算法较为简单，而且漏洞很大，只要稍微炮制一下，就可以让网页的排名很高，从而使得传统的排名算法毫无用处。谷歌依靠着链接分析技术改变了这一现状，使得搜索技术得到了一个质的提升，谷歌也因此成为世界首屈一指的IT互联网公司。

谷歌的排名算法被称为PageRank算法。其基本思路是将网页间的超链接视为一种推荐或认可。下面我们用一个例子说明该算法：

假设有五个网页，链接如图所示！

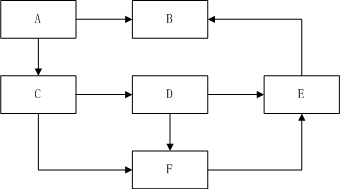
链接矩阵为：

	A	B	C	D	E	F
A		1/2	1/2
B
C				1/2		1/2
D					1/2	1/2
E		1
F					1

如果网页i有外链指向网页j，则矩阵的ij处不为0，否则为0。另外，如果网页i的外链结合为{a,b,c,d,…}，集合大小为k，则矩阵ia,ib,ic…的值都为1/k。

由矩阵可以看出，矩阵中有很多0，矩阵中所有的值都不大于1，矩阵的每一行的和都为1或0，矩阵中一行全为0的行所表示的网页节点称为悬孤节点。

假设网页的权重由向量P表示，P为1*N的向量，N为网页总数，则PageRank用来计算网页权重的迭代公式为p(k+1)=p(k)*H，H即为上述所说的链接矩阵，k为迭代次数。重复计算公式直到p(k)和p(k+1)的差距足够小，就得到了各个网页的权重，从而可以排序。PageRank值也可以和原来的简单索引时的权重进行组合得到最后的权重。

悬孤节点和随机跳转

当然，直接进行PageRank迭代是有问题的。比如上面的矩阵中为0的那一行，会让B的权重为0。需要考虑两个问题，第一个是悬孤节点的处理，我们引入随机跳转，即悬孤节点到其他网页的概率都为1/N，N为网页的总数。第二个是随机跳转的问题，用户打开网页不一定总是从上一个网页点进去的，也可能是随意的跳转，这就需要引入一个新的参数alpha，称为阻尼系数，即矩阵中不为0的值的概率都乘以alpha，为0的概率值改为(1-alpha)/N，N为网页总数。

Alpha接近于1时，PageRank值会逐渐接近浏览者完全跟随链接访问网页对应的结果，alpha接近于0时，PageRank值接近于1/N。随着alpha的增长，迭代次数也会增大，因而alpha也是所选择的web结构和算法性能之间的平衡。根据资料，google现在的alpha值为0.85。

迭代中止条件

那么迭代算法中如何衡量迭代前后网页权重向量P的差距呢？迭代前后两个向量的差距就是各个分量的差的绝对值之和。停止条件阈值的选择也会影响最后的结果。收敛后的各个网页的pagerank值的差别与停止阈值的最小值处于同一个数量级，因此，要根据阈值将所有的网页都区分开，阈值需要足够小，若有100个网页，则阈值要小于0.01才行，要是有10¹⁰个网页，则阈值要小于10^-10。

用户反馈

还有一个重要的因素就是用户的反馈，对于一个搜索串来说，不同的用户的点击条目是不同的，即便是同一个用户，在不同时间可能点击条目也是不同的。比如‘换届’这个搜索，中国人可能点击十八大，美国人可能点击美国大选，英国人可能点击英国大选等；再比如‘汶川地震’，可能先会关注它的抢救信息，后面会关注它的重建信息等，但在一般情况下，搜索引擎很难获取用户id；而时间因素则可以通过训练近一段时间的数据来保持时效性。

对于用户点击反馈，可以使用朴素贝叶斯分类器进行权重计算。朴素贝叶斯公式如下：

P(X|Y)=P(Y|X)*P(X)/P(Y)

其中，P(X)为观察到X的概率，也称为先验概率；P(Y|X)为X条件下Y发生的概率，也成为似然概率；P(Y)为一般情况下选到Y的概率，被称为证据，在一般情况下，由于其是随机的，不考虑。P(X|Y)则为Y条件下X发生的概率。

在这里，P(X|Y)表示用户搜索Y时想点击X的概率；P(X)表示X的概率，一般情况下，每个网页只出现一次，但是有些情况，比如转载博客，使得相同的内容出现了多次；P(Y|X)表示点击了X的各个搜索串中，Y的概率。

为啥不直接计算P(X|Y)呢？因为不能算啊。搜索记录中只记录了用户的搜索串和点击的条目，没有记录在某搜索串下有多少个条目可以选择。因为一般情况下用户看到搜索引擎提供的前几个结果就已经选择要点击哪个了，而我们无法确定用户是从多少个结果中选择的。所以只能通过朴素贝叶斯估计。

对于一次搜索来说，在PageRank值上加上条件概率作为新的PageRank值，就考虑进了用户点击的影响，当然，也可以使用其他的公式进行组合。

DocRank

到这里，网页的PageRank计算就叙述结束了。对于word、pdf等没有外链的文档，如何排名呢？

解决方案就是先将文档进行分词，表示成为一个词语向量，对于两个文档来说，求出交集，对于交集中的每个词，计算在两个文档中出现次数的比值的正切函数值，再对所有词取和，将该值当做文档到文档的外链值。

衡量结果

那么如何衡量信息检索的结果呢？最常用的两个指标是精确度和查全率。精确度就是获取的相关文件的数量除以获取的文件总数。查全率就是获取的相关文件的数量除以相关文献的总数。通俗点说就是，精确度回答了‘我得到的结果中有多少是我想要的？’，查全率则回答了“我得到了所有我能得到的结果吗？”。

扩展阅读：优化PageRank算法

PageRank算法在大数据时会遇到很多问题，比如，矩阵根本不能完全载入到内存，迭代次数多，需要耗费的时间很长等；在这种情况下，可以通过改进数据结构，加速PageRank的计算，使用分布式IO系统等方法提高计算的性能。

将矩阵用邻接表表示，可以大大降低矩阵的占用空间，还可以参考编码或其他技术进一步压缩邻接表（参考文献中Boldi和Vigna的论文）。

也有人提出将悬孤节点先去掉，待PageRank值收敛到一定程度再添加进来，但是这样做就不公平了，为了兼顾效率和公平，使用基于跳转矩阵H的对称性的方法（参考文献中Langville和Meyer的文章）。

PageRank的加速技术还包括Kamvar的二次外插技术——Aitken外插法（extrapolation），以及更加高级的切比雪夫（Chebyshev）多项式谱方法为代表的谱方法。这些方法的目的是在两次迭代之间得到一个更好的PageRank的近似。

大规模计算方面，自然就是近期火的不能再火的基于map-reduce的hadoop了。

参考文献

转载：http://blog.csdn.net/zhoubl668/article/details/9533109