A*算法最优解提取算法

EmilMatthew ([email protected])      

[ 类别 ]算法，人工智能

[推荐指数]★★★★

[ 摘要  ]本文就“ 启发式搜索算法引论 ------A* 算法理论与实践 ” 一文中的最优解提取算法的不足处进行了改进，提出了一个通用的 A* 算法的最优解提取算法。

[ 关键词 ] A* ，最优解提取， AS2

            The Algorithm of Best Answer Getting Method in A*

[Classify] Algorithm ,  Artificial Intelligence

[   Level ] ★★★★

[Abstract]In my previous passage------” Introduction to Heuristics Search------A* Algorithm Principle and Practice”, the algorithm for getting out the best answer of A* has some drawbacks when meets some certain conditions. In this article, I introduce a general algorithm for best answer getting in A* algorithm.

[Key Words] A* , Best Answer Getting , AS2

 

[1缺点回顾]

   首先，要向对我的上一篇文章“ 启发式搜索算法引论------A*算法理论与实践 ”提出批评意见的两位网友 7heaven,Ourme 表示感谢。上篇文章的算法实现中，有时在某些位置，去走向特定点时，会出现主角走小弯路的现象（当然，还是可以走到最终点的），起初，我并不太在意，现在经过仔细的思考后，发现前面所用的提取最优路径的算法有些不足 （ A* 算法本身并没有任何问题） 。主要的问题出在对 CLOSE 表进行最优路径提取时，有些走弯路的点亦被包含进去了，而用前文的算法思路，是无法解决这一问题的。

 

[2 算法核心 ]

       前文算法之最大不足，就是仅仅利用 CLOSE Table 来存储搜索过程信息，最终进行逆向提取。而问题的关键，就在于仅仅利用 CLOSE Table ，并不 总能 从中提取出搜索问题的最优解 , ，并且，提取时的一些舍去点的原则要根据不同的搜索问题来设计，无通用性可言。当我把目光再放到 A* 搜索过程的搜索树上时，发现每个结点的父结点大有可为，经过一阵试探及思考后，得到了这个并不复杂的最优解提取算法。

       首先，对于 A* 算法在搜索过程形成的搜索树，可以得到如下性质：

       从最终结点 pEnd 开始，向其父结点 pEnd.parent 回溯，再由其父结点向其父结点 pEnd.parent.parent 回溯 … …, 显然，最终将到达初始点。由归纳法易证，该条通路上的所有结点均在且仅这些点在最优搜索解路径上。

       有了这个性质，再结合父结点表和 CLOSE Table 两张表，即可非常轻松的得到最优解了。先请看三个该算法的示例：

   

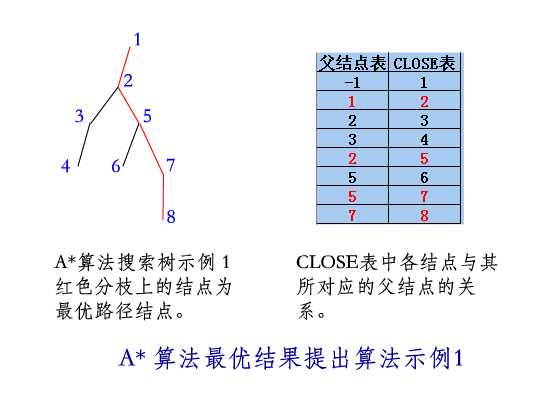
                                                    A* 算法最优解提取算法示例 1

 

A* 算法最优解提取算法示例 2

 

A* 算法最优解提取算法示例 3

 

       所以，并不难得出下面的 A* 算法最优解提取算法框架（ 注意边界情况的处理 ）：

       CIndex : a valuable identifies current element position in CLOSE Table

       CLOSE Table: note all the node which is searched in searching sequence

       Parent Table :note all the searched node’s parent node searching sequence.

NA Table: note the best answer ------from end node to start node.

NAIndex: index for NATable

 

//Init

Index   <-Rear position for CLOSE Table

NAIndex<-0

While(true)

       {

                     NATable[NAIndex]=Parent Table[CIndex]

                           

                     NAIndex<-NAIndex+1;

                     CIndex <- CIndex-1;

                                  

                     if(CIndex==0) //Normal Successful Exit Node

                                   break;

                                  

                     while(NATable[NAIndex-1] is not equal to Parent Table[CIndex] )

                     {

                                   CIndex --;

                     }

                    

                     if(CIndex==0) //Special condition for exit out

                     {

                                   NATable[NAIndex]=Parent Table[CIndex]

NAIndex++;

                                   break;

                     }      

}

      

       具体实现请参考前文 ( 已更新 )

 

[3 交互式实现 ]

               

                                            

测试1  

   

 

                                                                     测试2