deep learning Softmax分类器(L-BFGS,CG,SD)
前言:
在最优化计算方法中,我已经讲到了机器学习常用的一些参数优化的方法,如梯度法,共轭梯度法,牛顿法,拟牛顿法,在《最优化计算方法》板块,我都用回归分析比较了这些参数优化的方法,从现在开始,我将把这些参数优化的方法用来训练分类器。
在本节中,我讲介绍softmax分类器,该分类器是在logistic回归模型在多分类问题上的推广。在多分类问题中,分类标签y可以取两个以上的值。softmax分类器对于诸如MNIST手写数字分类等问题上有很好的效果,该问题就是识别不同的单个数字和图像(可以应用于车牌识别、目标检测等方向),softmax回归时有监督,后面我会介绍它在deep learning中的应用,对于以后我介绍的分类器我都将用到MNIST这个手写数字识别库,第一,方便我们比较不同分类器的效果,第二,这个数据库比较经典完善。http://yann.lecun.com/exdb/mnist/
同时我会讲Steepest Descent(SD)、CG方法、L-BFGS这些调参方法对识别效果的影响。
softmax简介
我们的训练集有m个已标记的样本构成:{(x(1),y(1)),...,(x(m),y(m))},输入特征是n+1维的,其中x_0代表截距项,也就是通常所说的偏置。在softmax回归中,我们解决的是多分类的问题,类标y可以去k个不停的值。因此,对于训练集{(x(1),y(1)),...,(x(m),y(m))},我们有,分类的时候0替换为10。在MNIST数字识别的任务中,我们有k=10个不同的类别。
对于给定的测试输入x,我们想用假设函数针对每一类别j估算出概率值p(y=j|x)。也就是说,我们想估计x的每一种分类结果出现的概率。因此,我们的假设函数将要输入一个k维的向量(向量元素的总和为1)来表示这k个估计的概率值。具体地说,我们的假设函数![]() 形式如下:
形式如下:
其中 是模型的参数。请注意 这一项对概率分布进行归一化,使得所有的概率之和为1。
这一项对概率分布进行归一化,使得所有的概率之和为1。
为了方便起见,我们同样的使用符号θ来表示全部的模型参数。在实现softmax回归时,将θ用一个k×(n+1)的矩阵来表示会很方便的,该矩阵是将 按列罗列起来的,如下所示:
代价函数
现在我们来介绍softmax分类器中的代价函数。在下面的公式中,1{·}是示性函数,其取值规则为:1{值为真的表示式}=1,1{值为假的表达式} =0.举例来说明1{1+1=2}=1,1{1+1=3}=0,我们的代价函数可以表示如下:
熟悉logistic回归的读者都知道,softmax的损失函数和logistic的损失函数非常类似,只是在softmax损失函数中对类标记的k个可能值进行累加。注意在softmax回归中将x分类为类别j的概率为:
可以用如下图例进行表示,类似于神经网络,只是少了一层隐含层。
输出最大值概率值则属于相应的类,比如说,p1最大,就属于第一类,这个网络在后续的CNNs中会用到。
对于J(θ)的最小化问题,目前还没有闭式的解法,因此,我们使用迭代优化算法(SD,CG,L-BFGS)。经过求导,我们得到梯度公式如下:
有了上面的偏导数公式之后,我们就可以将它带入到这些参数优化的算法中去,进而来优化J(θ)。例如,在梯度下降的标准实现中,每一次迭代需要进行如下更新: ![]() (
(![]() )。
)。
softmax回归模型参数化的特点
Softmax分类器有一个不寻常的特点:它有一个“冗余”的参数集。为了便于阐述这一特点,假设我们从参数向量 中减去了向量 ![]() ,这时,每一个 都变成了
,这时,每一个 都变成了 ![]() (
(![]() )。此时假设函数变成了以下的式子:
)。此时假设函数变成了以下的式子:
换句话说,从 中减去 ![]() 完全不影响假设函数的预测结果!这表明前面的softmax分类器中存在冗余的参数。更正式一点来说,Softmax分类器被过度参数化了。对于任意一个用于拟合数据的假设函数,可以求出多组参数值,这些参数得到的是完全相同的假设函数 。
完全不影响假设函数的预测结果!这表明前面的softmax分类器中存在冗余的参数。更正式一点来说,Softmax分类器被过度参数化了。对于任意一个用于拟合数据的假设函数,可以求出多组参数值,这些参数得到的是完全相同的假设函数 。
进一步而言,如果参数 是代价函数 ![]() 的极小值点,那么
的极小值点,那么 ![]() 同样也是它的极小值点,其中
同样也是它的极小值点,其中 ![]() 可以为任意向量。因此使
可以为任意向量。因此使 ![]() 最小化的解不是唯一的。(有趣的是,由于
最小化的解不是唯一的。(有趣的是,由于 ![]() 仍然是一个凸函数,因此梯度下降时不会遇到局部最优解的问题。但是 Hessian 矩阵是奇异的/不可逆的,这会直接导致采用牛顿法优化就遇到数值计算的问题)
仍然是一个凸函数,因此梯度下降时不会遇到局部最优解的问题。但是 Hessian 矩阵是奇异的/不可逆的,这会直接导致采用牛顿法优化就遇到数值计算的问题)
注意,当 ![]() 时,我们总是可以将
时,我们总是可以将 ![]() 替换为(即替换为全零向量),并且这种变换不会影响假设函数。因此我们可以去掉参数向量
替换为(即替换为全零向量),并且这种变换不会影响假设函数。因此我们可以去掉参数向量 ![]() (或者其他 中的任意一个)而不影响假设函数的表达能力。实际上,与其优化全部的
(或者其他 中的任意一个)而不影响假设函数的表达能力。实际上,与其优化全部的 ![]() 个参数 (其中
个参数 (其中 ![]() ),我们可以令
),我们可以令 ![]() ,只优化剩余的
,只优化剩余的 ![]() 个参数,这样算法依然能够正常工作。
个参数,这样算法依然能够正常工作。
在实际应用中,为了使算法实现更简单清楚,往往保留所有参数 ![]() ,而不任意地将某一参数设置为 0。但此时我们需要对代价函数做一个改动:加入权重衰减。权重衰减可以解决 softmax分类的参数冗余所带来的数值问题。
,而不任意地将某一参数设置为 0。但此时我们需要对代价函数做一个改动:加入权重衰减。权重衰减可以解决 softmax分类的参数冗余所带来的数值问题。
我们通过添加一个权重衰减项 ![]() 来修改代价函数,这个衰减项会惩罚过大的参数值,现在我们的代价函数变为:
来修改代价函数,这个衰减项会惩罚过大的参数值,现在我们的代价函数变为:
有了这个权重衰减项以后 (![]() ),代价函数就变成了严格的凸函数,这样就可以保证得到唯一的解了。 此时的 Hessian矩阵变为可逆矩阵,并且因为
),代价函数就变成了严格的凸函数,这样就可以保证得到唯一的解了。 此时的 Hessian矩阵变为可逆矩阵,并且因为![]() 是凸函数,梯度下降法和L-BFGS等算法可以保证收敛到全局最优解。
是凸函数,梯度下降法和L-BFGS等算法可以保证收敛到全局最优解。
为了使用优化算法,我们需要求得这个新函数 ![]() 的导数,如下:
的导数,如下:
通过最小化 ![]() ,我们就能实现一个可用的softmax 分类器。
,我们就能实现一个可用的softmax 分类器。
下面只给出softmax-L-BFGS的代码。
%% STEP 0: Initialise constants and parameters
%
% Here we define and initialise some constants which allow your code
% to be used more generally on any arbitrary input.
% We also initialise some parameters used for tuning the model.
inputSize = 28 * 28; % Size of input vector (MNIST images are 28x28)
numClasses = 10; % Number of classes (MNIST images fall into 10 classes)
lambda = 1e-4; % Weight decay parameter
itera_num=200;
Jtheta = zeros(itera_num, 1);
a=1;roi=0.5;c=0.6;m=10;
%%======================================================================
%% STEP 1: Load data
images = loadMNISTImages('train-images.idx3-ubyte');
labels = loadMNISTLabels('train-labels.idx1-ubyte');
labels(labels==0) = 10; % Remap 0 to 10
inputData = images;
DEBUG = false;
if DEBUG
inputSize = 8;
inputData = randn(8, 100);
labels = randi(10, 100, 1);
end
theta = 0.005 * randn(numClasses * inputSize, 1);%输入的是一个列向量
% Randomly initialise theta
theta = reshape(theta, numClasses, inputSize);%将输入的参数列向量变成一个矩阵
numCases = size(inputData, 2);%输入样本的个数
groundTruth = full(sparse(labels, 1:numCases, 1));%这里sparse是生成一个稀疏矩阵,该矩阵中的值都是第三个值1
%稀疏矩阵的小标由labels和1:numCases对应值构成
cost = 0;
thetagrad = zeros(numClasses, inputSize);
%% STEP 2: Implement softmaxCost
p = weight(theta,inputData);
cost(1) = -1/numCases * groundTruth(:)' * log(p(:)) + lambda/2 * sum(theta(:) .^ 2);
thetagrad = -1/numCases * (groundTruth - p) * inputData' + lambda * theta;
B=eye(numClasses);
H=-inv(B);
d1=H*thetagrad;
theta_new=theta+a*d1;
theta_old=theta;
fprintf('%10s %10s %15s %15s %15s','Iteration','cost','Accuracy');
fprintf('\n');
%% Training
for i=2:itera_num %计算出某个学习速率alpha下迭代itera_num次数后的参数
a=0.5;
theta_new=reshape(theta_new, numClasses,inputSize);
theta_old=reshape(theta_old,numClasses,inputSize);
p=weight(theta_new,inputData);
Mp=weight(theta_old,inputData);
cost(i)=-1/numCases * groundTruth(:)' * log(p(:)) + lambda/2 * sum(theta_new(:) .^ 2);
thetagrad_new = -1/numCases * (groundTruth - p) * inputData' + lambda * theta_new;
thetagrad_old = -1/numCases * (groundTruth - Mp) * inputData' + lambda * theta_old;
thetagrad_new=reshape(thetagrad_new,numClasses*inputSize,1);
thetagrad_old=reshape(thetagrad_old,numClasses*inputSize,1);
theta_new=reshape(theta_new,numClasses*inputSize,1);
theta_old=reshape(theta_old,numClasses*inputSize,1);
M(:,i-1)=thetagrad_new-thetagrad_old;
BB(:,i-1)=theta_new-theta_old;
roiJ(i-1)=1/(M(:,i-1)'*BB(:,i-1));
gamma=(BB(:,i-1)'*M(:,i-1))/(M(:,i-1)'*M(:,i-1));
HK=gamma*eye(inputSize*numClasses);
r=lbfgsloop(i,m,HK,BB,M,roiJ,thetagrad_new);
d=-r;
d=reshape(d,numClasses,inputSize);
theta_new=reshape(theta_new,numClasses,inputSize);
theta_old=theta_new;
theta_new = theta_new + a*d;
%% Test the Accuracy
images = loadMNISTImages('t10k-images.idx3-ubyte');
labels = loadMNISTLabels('t10k-labels.idx1-ubyte');
labels(labels==0) = 10;
inputDatatest = images;
pred = zeros(1, size(inputData, 2));
[nop,pred]=max(theta_new*inputDatatest);
acc(i-1) = mean(labels(:) == pred(:));
acc(i-1)=acc(i-1) * 100;
%%
fprintf('%5d %13.4e %0.3f%%\n',i,cost(i),acc(i-1));
end
plot(0:199, cost(1:200),'b--','LineWidth', 3);
figure
plot(1:199,acc(1:199),'b--','LineWidth',3);
%%
legend('softmax-SD','softmax-L-BFGS');
xlabel('Number of iterations')
ylabel('Cost function')
==============================================================================================
下节讲sparse autoencoder softmax分类器,敬请期待!
==============================================================================================怀柔风光

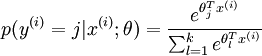

![\begin{align}\nabla_{\theta_j} J(\theta) = - \frac{1}{m} \sum_{i=1}^{m}{ \left[ x^{(i)} ( 1\{ y^{(i)} = j\} - p(y^{(i)} = j | x^{(i)}; \theta) ) \right] } + \lambda \theta_j\end{align}](http://img.e-com-net.com/image/info5/2f482623946e4e36a95cc7fc86c5919b.png)
