Google Code Jam 2012 Qualification Round. Problem D. Hall of Mirrors

  Google Code Jam，由google发起的一个网络算法竞赛，一0年的时候参加过一次，只进了Round 2，那时我已经大三了。现在，我已经工作快两年了（到今年7月）。

  一0年还参加过一次百度举行的“百度之星”的网络竞赛，也算是算法竞赛，那次进了复赛前400名，拿了件T恤。为了让人生稍微完整一些，于是准备今年的GCJ，希望能拿到一件google T恤也就满意了。

  两年没写算法了（工作中完全不用算法），生疏得很多C语言的语法都忘记了，惭愧啊，记忆这鬼东西很珍贵。上周拿去年的GCJ题目来练习，从Qualification Round开始做，到D题卡主了，想了很长时间，脑子不行了。翻看了solution和网上的一些提示，最后在今天把它过了。这个题目最难想的就是模拟部分，可以试想到如果在比赛时候遇到此题，即使能想到思路估计也只能无奈放弃，因为实在太多的细节需要拿捏，且在加之调试时间，恐怕3个小时早已经过去了。

  题目连接。

=> 思路：

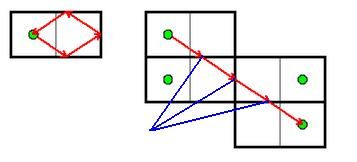
  此题的中心思想就是镜面反射原理，我们截取google solution里面的图片用用：

沿镜面对折我们发现可以将折痕还原到最初的二维空间中，而翻开后的直线就是可以两点可以到达的路线，因此确定了光线的角度，就可以模拟光线的反射行为，最终到达目的点，这个很关键。

  对于不规则的二维空间如何来确定光线的初始角度呢？其实思路还是一样，镜面原理。

1. A图和B图是对称的。

2. a点和a'点是对称的。

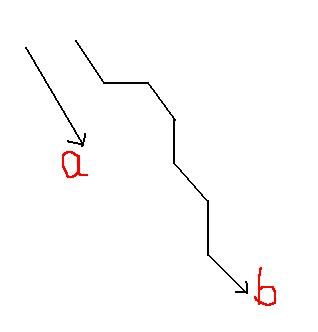
不难发现，不规则的二维空间也可以利用镜面原理将二维空间对折，于是光线又是直线了。这样我们就可以证明一个非常重要的想法：到达目的点的光线方向必定是由起始点与一个整数点确定的。

  从上图我们可以知道目的点b点和a点的关系，b = a + (x,y)，(x,y)是矢量方向且值为整数，由于b为整数点，所以证明了a点必为整数点。有了这个理论做基础，我们就可以开始枚举光线的方向来模拟是否可以到达目的点。

  想到了上面的思路，才能继续下面的模拟部分，若整个题目需要1个小时的话，上面的部分可能只占到不到5分钟时间，因此可想而知模拟部分需要花多少时间和代价了。

=> 模拟：

  一个好的模拟方法既可以保证思路的通畅又可以改善程序的时间效率甚至是调试难度。

  试想一下，如果光线在传输的过程中没有镜面的干预是什么情况，光线会一条直线走到底。但是有了镜子的加入，我们需要光线做一些情况的预判和分析，我们可以分为两个大类：

1. 射到角落里了。

2. 射到镜面上了。

在开始分析之前，我们需要明白一旦光线的方向确定之后，光线的方向就不会改变，因为我们可以通过对折的方式将光线逼直，因此整个原始的二维空间其实就可以类似4象限一样分布在东南、东北、西南和西北了。

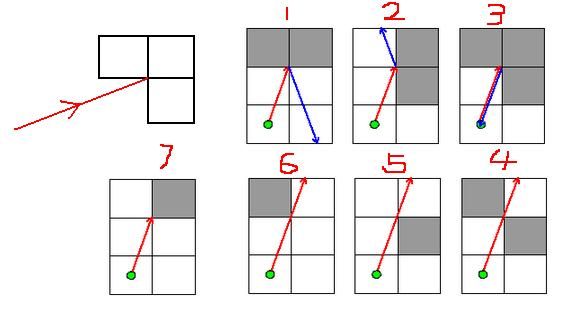
第一类：射到角落里。

  这分为7中情况，如下图：

如何计算撞到了角落的情况呢？

我们令(x0,y0)为起始点，(cx,cy)为当前的G点，(px,py)为向上和向右的方向（如(-1,1)表示X轴的负方向，Y轴的正方向），(dx,dy)为该光线的方向。因此就有条件计算公式了：dy*((cx-x0)*2+px) == dx*((cy-y0)*2+py)。

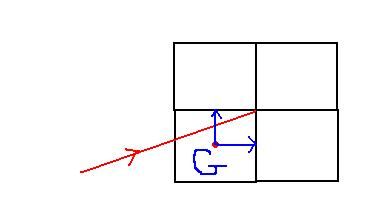
第二类：射到镜面上。

  它只有两种情况，如下图：

这里就有发挥各位的数学基础了，只需判断一个情况即可。公式我就不推导了，注意一些细节处理喔~

  OK，把上面的情况考虑完了，算法框架就快成型了，不过不急还差一步，就是下一个G点怎么得到，如何利用对折来确定G点呢？这里又可以分为两种情况：

1. 以X轴对折处理。

2. 以Y轴对折处理。

通过上面的分析，我们已经可以判断出光线会碰到的谁的镜子了，对折机制我们只说一种即可，另外一种一样的处理方式，我们来讲述一下“以X轴对折处理”方式。

看到上面的图示，估计大家已经有想法了吧，就是将原来的G点按照X轴做一个反向即可，即G' = -G。哈哈！不过，千万不要忘记移动你的起始点(x0',y0') = (x0,y0) + (G'-G)。

  好了，有了这些分析，最后就是自己把code组织好，等着调试咯~。这道题的确非常磨人，考验耐心和你的琢磨程度。可是就是这样的题目做着才爽，当correct的刹那间，你会发现自己好像升天了！

  Google Code Jam 2013 Qualification Round的北京时间是：2013/04/13 星期六 07:00，持续25小时。

附上D题代码：

#include <stdio.h>
#include <strings.h>
#include <math.h>

//#define D_DEBUG

#ifdef D_DEBUG
#define dprintf(...) fprintf(stderr,__VA_ARGS__)
#else
#define dprintf(...)
#endif

char mirror[30][31];

int gcd(int a,int b)
{
	a = abs(a);
	b = abs(b);
	while(b) {
		int t = a%b;
		a = b;
		b = t;
	}
	return a;
}

int ray(int x0,int y0,int dx,int dy,int dist)
{
	int px,py,cx,cy,mx,my;
	
	/* step contain sign */
	px = dx ? dx/abs(dx):0;
	py = dy ? dy/abs(dy):0;
	
	/* current position */
	cx = x0, cy = y0;

	/* my source position */
	mx = x0, my = y0;

	while(1) {
		dprintf("(%d,%d)->(%d,%d) ",x0,y0,cx,cy);
		/* compute ray to corner*/
		int is_corner =0;
		int corx=0,cory=0;
		if (dx && dy)
			if (dy*(corx=((cx-x0)*2+px)) == dx*(cory=((cy-y0)*2+py)))
				is_corner =1;

		if (is_corner) {
			dprintf("(is corner) ");
			/* x#
			 *  x
			 */
			if (mirror[abs(cy+py)][abs(cx+px)]=='#') {
				/* ##
				 *  #
				 */
				if (mirror[abs(cy+py)][abs(cx)]=='#'
						&& mirror[abs(cy)][abs(cx+px)]=='#') {
					if (corx*corx + cory*cory <= dist*dist) {
						dprintf("\nsuccuss:back ray!\n");
						return 1;
					}
					else {
						dprintf("(%d,%d)->(%d,%d) (fail:back ray out of dist) ",
								x0,y0,cx,cy);
						break;
					}
				}
				/* ##
				 *  .
				 */
				else if (mirror[abs(cy+py)][abs(cx)]=='#') {
					y0 += (-(cy+py)+py-(cy+py));
					cx += px, cy = (-(cy+py)+py);
				}
				/* .#
				 *  #
				 */
				else if (mirror[abs(cy)][abs(cx+px)]=='#') {
					x0 += (-(cx+px)+px-(cx+px));
					cy += py, cx = (-(cx+px)+px);
				}
				/* .#
				 *  .
				 */
				else {
					dprintf("\n(fail:corner!)\n");
					break;
				}
			}
			/* x.
			 *  x
			 */
			else {
				cx += px;
				cy += py;
			}
		}
		else {
			/* compute ray to Y direction */
			int m = dx*(cy*2+py-y0*2)+dy*(x0*2+cx/abs(cx));
			int n = 2*dy;
			if (dy && m/n == cx) {
				cy += py;
				if (mirror[abs(cy)][abs(cx)]=='#') {
					dprintf("(%d,%d)=# ",cx,cy);
					y0 += (-cy+py-cy);
					cy = -cy+py;
				}
				dprintf("Y ");
			}
			/* compute ray to X direction */
			else {
				cx += px;
				if (mirror[abs(cy)][abs(cx)]=='#') {
					dprintf("(%d,%d)=# ",cx,cy);
					x0 += (-cx+px-cx);
					cx = -cx+px;
				}
				dprintf("X ");
			}
		}
		/* check if succuss */
		if((cx-x0)*(cx-x0)+(cy-y0)*(cy-y0) <= dist*dist) {
			if (dx*(cy-y0) == dy*(cx-x0) && (mx==abs(cx) && my==abs(cy))) {
				dprintf("\n(%d,%d)->(%d,%d) succuss:normal!\n",
						x0,y0,cx,cy);
				return 1;
			}
		}
		else {
			dprintf("\n(%d,%d)->(%d,%d) (fail:out of dist)\n",
					x0,y0,cx,cy);
			break;
		}
	}
	return 0;
}

int main()
{
	int T,cas;
	scanf("%d",&T);
	dprintf("start...\n");
	for (cas=1;cas<=T;cas++)
	{
		int h,w,d,i,j,x0,y0,cnt;
		printf("Case #%d: ",cas);
		dprintf("\nCase %d:\n",cas);
		scanf("%d %d %d",&h,&w,&d);
		for (i=0;i<h;i++) {
			scanf("%s",mirror[i]);
			for (j=0;j<w;j++)
				if (mirror[i][j]=='X')
					x0=j,y0=i;
		}
		cnt =0;
		for (i=-d;i<=d;i++)
			for(j=-d;j<=d;j++)
				if ((i || j) && (i*i+j*j <= d*d)
						&& gcd(i,j)==1) {
					dprintf("the %d ray:(x0,y0)=(%d,%d) "
							"(dx,dy)=(%d,%d) d=%d\n",cnt,x0,y0,i,j,d);
					cnt += ray(x0,y0,i,j,d);
				}
		printf("%d\n",cnt);
	}
}