深度优先算法,图的遍历
和树的遍历相似,若从图中某顶点出发访遍图中每个顶点,且每个顶点仅访问一次,此过程称为图的遍历(Traversing Graph)。图的遍历算法是求解图的连通性问题、拓扑排序和求关键路径等算法的基础。图的遍历顺序有两种:深度优先搜索(DFS)和广度优先搜索(BFS)。对每种搜索顺序,访问各顶点的顺序也不是唯一的。
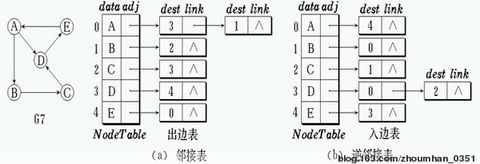
1、邻接表及逆邻接表的存储方法
(1)定义
邻接表是图的一种链式存储结构。类似于树的孩子链表表示法。在邻接表中为图中每个顶点建立一个单链表,用单链表中的一个结点表示依附于该顶点的一条边(或表示以该顶点为弧尾的一条弧),称为边(或弧)结点。特征如下:
1) 为每个顶点建立一个单链表,
2) 第i个单链表中包含顶点Vi的所有邻接顶点。
把同一个顶点发出的边链接在同一个边链表中,链表的每一个结点代表一条边,叫做表结点(边结点),邻接点域adjvex保存与该边相关联的另一顶点的顶点下标 , 链域nextarc存放指向同一链表中下一个表结点的指针 ,数据域info存放边的权。边链表的表头指针存放在头结点中。头结点以顺序结构存储,其数据域data存放顶点信息,链域firstarc指向链表中第一个顶点。

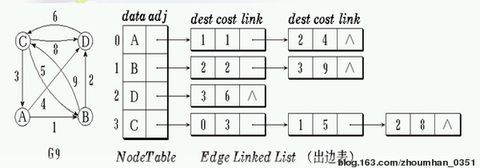
带权图的边结点中info保存该边上的权值。
顶点 Vi 的边链表的头结点存放在下标为 i 的顶点数组中。
在邻接表的边链表中,各个边结点的链入顺序任意,视边结点输入次序而定。
设图中有 n 个顶点,e 条边,则用邻接表表示无向图时,需要 n 个顶点结点,2e 个边结点;用邻接表表示有向图时,若不考虑逆邻接表,只需 n 个顶点结点,e 个边结点。
建立邻接表的时间复杂度为O(n*e)。若顶点信息即为顶点的下标,则时间复杂度为O(n+e)。
(2)邻接表的示例及逆邻接表
在有向图的邻接表中,第 i 个链表中结点的个数是顶点Vi的出度,表结点的adjvex存储的是以当前头结点为弧尾的弦。在所有链表中其邻接点域的值为i的结点的个数是顶点vi的入度。
在有向图的逆邻接表中,第 i 个链表中结点的个数是顶点Vi 的入度,表结点的adjvex存储的是以当前头结点为弧首的弦。
如下为带权图的邻接表:
2、深度优先算法思想
深度优先搜索遍历类似于树的先序遍历。假定给定图G的初态是所有顶点均未被访问过,在G中任选一个顶点i作为遍历的初始点,则深度优先搜索递归调用包含以下操作:
(1)访问搜索到的未被访问的邻接点;
(2)将此顶点的visited数组元素值置1;
(3)搜索该顶点的未被访问的邻接点,若该邻接点存在,则从此邻接点开始进行同样的访问和搜索。
深度优先搜索DFS可描述为:
(1)访问v0顶点;
(2)置 visited[v0]=1;
(3)搜索v0未被访问的邻接点w,若存在邻接点w,则DFS(w)。
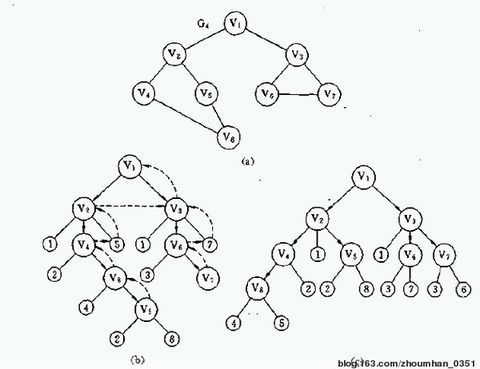
遍历过程:
DFS 在访问图中某一起始顶点 v 后,由 v 出发,访问它的任一邻接顶点 w1;再从 w1 出发,访问与 w1邻 接但还没有访问过的顶点 w2;然后再从 w2 出发,进行类似的访问,… 如此进行下去,直至到达所有的邻接顶点都被访问过的顶点 u 为止。
接着,退回一步,退到前一次刚访问过的顶点,看是否还有其它没有被访问的邻接顶点。如果有,则访问此顶点,之后再从此顶点出发,进行与前述类似的访问;如果没有,就再退回一步进行搜索。重复上述过程,直到连通图中所有顶点都被访问过为止。如下图所示:
3、深度优先算法C语言描述
4、深度优先算法C语言实现
#include "stdio.h"
#define MAX_VERTEX_NUM 10
#include "conio.h"
#include "stdlib.h"
typedef char VertexType;
typedef struct ArcNode{
int adjvex;
struct ArcNode *nextarc;
int info;
}ArcNode; //表结点类型
typedef struct VNode{
VertexType data;
ArcNode *firstarc;
}VNode,AdjList[MAX_VERTEX_NUM]; //头结点
typedef struct{
AdjList vertices; //邻接表
int vexnum,arcnum;
}ALGraph;
int visited[MAX_VERTEX_NUM];
int LocateVex(ALGraph G,char u)
{
int i;
for (i=0;i<G.vexnum;i++)
{ if(u==G.vertices[i].data) return i; }
if (i==G.vexnum) {printf("Error u!\n");exit(1);}
return 0;
}
void CreateALGraph_adjlist(ALGraph &G)
{
int i,j,k,w;
char v1,v2,enter;
ArcNode *p;
printf("Input vexnum & arcnum:\n");
scanf("%d",&G.vexnum);
scanf("%d",&G.arcnum);
printf("Input Vertices:\n");
for (i=0;i<G.vexnum;i++)
{ scanf("%c%c",&enter,&G.vertices[i].data);//注意点,解说
G.vertices[i].firstarc=NULL;
}//for
printf("Input Arcs(v1,v2,w)以回车分开各个数据:\n");
for (k=0;k<G.arcnum;k++)
{
scanf("%c%c",&enter,&v1);
scanf("%c%c",&enter,&v2);
scanf("%d",&w);
i=LocateVex(G,v1);
j=LocateVex(G,v2);
p=(ArcNode*)malloc(sizeof(ArcNode));
p->adjvex=j;
p->info = w;
p->nextarc=G.vertices[i].firstarc;
G.vertices[i].firstarc=p;
}//for
return;
}//CreateALGraph_adjlist
void DFS(ALGraph &G, int v)
{
ArcNode *p;
printf("%c",G.vertices[v].data);
visited[v]=1;
p=G.vertices[v].firstarc;
while (p)
{ if (!visited[p->adjvex]) DFS(G,p->adjvex);
p=p->nextarc;
}
} //从第v个顶点出发DFS
void DFSTraverse(ALGraph &G)
{
for (int v=0;v<G.vexnum;++v)
visited[v]=0;
for (int v=0;v<G.vexnum;++v)
if (!visited[v]) DFS(G,v);
}//DFSTraverse
int main()
{
ALGraph G;
CreateALGraph_adjlist(G);
DFSTraverse(G);
}
5、注意点
(1)强制转换:p=(char*)&a;
(2)字符输入中,赋值顺序和缓存的联系
scanf是从标准输入缓冲区中读取输入的数据,如果连续输入两个%c格式的字符,而中间又要涉及回车,那么第二个字符将被赋予回车。
解决办法:
1、清空输入缓冲区
第一个scanf后加入语句:fflush(stdin); //C语言清空输入缓冲区函数
2、格式控制中加入空格
将第二个scanf改为:scanf(" %c",&ch2);//在%号前面加一个空格
scanf格式输入时要求输入格式与格式控制符中的完全一样(如:scanf("abcd%c",&ch);输入时必须输入abcde,ch得到的值为e)空格可以抵消前面输入的回车符。
3、直接用ch=getche()吸收回车
4、当输入完整数或字符时,后面还需要输入字符时,为了避免输入的字符变成回车符,可以在输入字符前多加一条scanf语句来吃掉前面的回车符。此时用来吃掉回车符的scanf输入可以用%c方式,也可以用%d方式。当用%c方式来吃掉回车符时,回车符被读进了char类型变量中,当用%d方式来吃掉回车符时,回车符并没有被送进int类型变量中,而是在异常的字符输入后,被自动清除了。
(3)我们这里,对图中各个顶点以单个字符来处理,当然也可以字符串来进行。对各个节点的访问,也仅仅是输出他们的节点名,当然还可以进一步的操作。