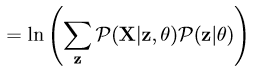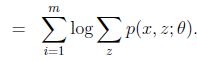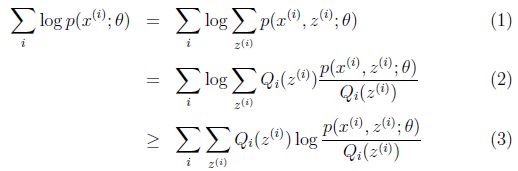斯坦福大学公开课 :机器学习课程(Andrew Ng)——11、无监督学习:the derivation of EM Algorithm
1)Convex Functions and Jensen’s inequality
2)Derivation of the EM-algorithm
1)Convex Functions and Jensen’s inequality
if f is a convex function, X is r.v, then: ![]() 。
。
特别地,![]() 当且仅当
当且仅当![]() ,也就是说X是常量。这里我们将
,也就是说X是常量。这里我们将![]() 简写为
简写为![]() 。
。
2)Derivation of the EM-algorithm
以下部分翻译自:http://www.seanborman.com/publications/EM_algorithm.pdf
EM算法是在有数据缺失的情况下或在存在隐含数据的情况下,计算极大似然估计(Maximum Likelihood (ML) estimate)的有效的迭代过程。在极大似然估计中,我们想要估计一个模型参数,以使已经观察到的数据有最大的概率出现。
EM算法每一个周期的迭代过程包括两步:E-step和M-step。E-step中,我们通过 已经观察到的数据和当前模型参数的估计 来估计缺失或隐含的数据;这个通过条件期望的计算实现。M-step中,假设上一步缺失/隐含数据的估计是正确的,并利用该“假设正确的缺失/隐含数据”代替“真正的缺失/隐含数据”极大化似然函数。
由于似然函数会随着每一次迭代递增,所以EM算法可以保证收敛!
下面是EM算法推导过程:
首先,给定的训练样本是![]() ,样例间独立,我们希望寻找θ实现最大化P(X|θ),即寻找θ的极大似然估计。
,样例间独立,我们希望寻找θ实现最大化P(X|θ),即寻找θ的极大似然估计。
其次,引入log likelihood function defined as:L(θ) = lnP(X|θ),最大化P(X|θ)和最大化L(θ) = lnP(X|θ)是一样的。
再次,定义隐含变量为Z,对于每一个样例i,让![]() 表示该样例隐含变量z的某种分布,
表示该样例隐含变量z的某种分布,![]() 满足的条件是
满足的条件是![]() 。(如果z是连续性的,那么
。(如果z是连续性的,那么![]() 是概率密度函数,需要将求和符号换做积分符号)。则L(θ) = lnP(X|θ)可以转换为:
是概率密度函数,需要将求和符号换做积分符号)。则L(θ) = lnP(X|θ)可以转换为:
接着,化简上式可得L(θ)如下:
我们说过,E步要假设“已经观察到的数据和当前模型参数的估计”都是已知,这里肯定是说(![]() 和
和![]() 都已知了),那么
都已知了),那么![]() 的值就决定于
的值就决定于![]() 和
和![]() 了。我们可以通过调整这两个概率使下界不断上升,以逼近
了。我们可以通过调整这两个概率使下界不断上升,以逼近![]() 的真实值,当不等式变成等式时,说明我们调整后的概率能够等价于
的真实值,当不等式变成等式时,说明我们调整后的概率能够等价于![]() 了。所以,我们当下要做的是找到等式成立的条件,根据Jensen不等式,要想让等式成立,需要让随机变量变成常数值,这里得到:
了。所以,我们当下要做的是找到等式成立的条件,根据Jensen不等式,要想让等式成立,需要让随机变量变成常数值,这里得到:
另外,我们知道![]() ,那么也就有
,那么也就有![]() ,对上式做进一步推导,那么有下式:
,对上式做进一步推导,那么有下式:
至此,我们推出了在固定其他参数![]() 后,
后,![]() 的计算公式就是后验概率,解决了
的计算公式就是后验概率,解决了![]() 如何选择的问题。这一步就是E步,建立
如何选择的问题。这一步就是E步,建立![]() 的下界。
的下界。
接下来的M步,就是在给定![]() 后,调整
后,调整![]() ,去极大化
,去极大化![]() 的下界(在固定
的下界(在固定![]() 后,下界还可以调整的更大)。
后,下界还可以调整的更大)。
那么一般的EM算法的步骤如下:
| 循环重复直到收敛 { (E步)对于每一个i,计算 (M步)计算 } |
EM算法收敛证明参考:http://www.cnblogs.com/jerrylead/archive/2011/04/06/2006936.html