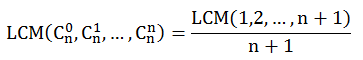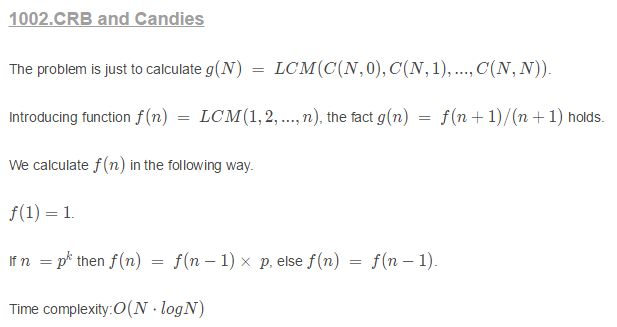HDU 5407 CRB and Candies(数学 素数表+预处理+快速幂+乘法逆元)——多校练习10

CRB and Candies

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)

Problem Description

CRB has  N  different candies. He is going to eat  K  candies.
He wonders how many combinations he can select.
Can you answer his question for all  K (0 ≤  K  ≤  N )?
CRB is too hungry to check all of your answers one by one, so he only asks least common multiple(LCM) of all answers.

 

Input

There are multiple test cases. The first line of input contains an integer  T , indicating the number of test cases. For each test case there is one line containing a single integer  N .
1 ≤  T  ≤ 300
1 ≤  N  ≤  106

 

Output

For each test case, output a single integer – LCM modulo 1000000007( 109+7 ).

 

Sample Input

   
   
   
   

    
    
    
    5
1
2
3
4
5
   
   
   
   

 

Sample Output

   
   
   
   

    
    
    
    1
2
3
12
10
   
   
   
   

 

Author

KUT（DPRK）

 

Source

2015 Multi-University Training Contest 10

 

/*********************************************************************/

可以说，该题是本场多校出题最快的一题了，做的人也挺多，但貌似就个人而言，觉得并不是一道简单的题，首先一个等价式就已经不知道了

再者最后用快速幂来处理除法取模的问题也是我目前还未知的。

题意：CRB有n颗不同的糖果，先在他要吃掉k颗(0<=k<=n)，问k取0~n的方案数的最小公倍数是多少

例如，现有3颗不同的糖果，他吃0颗有1种方案，1颗有3种方案，2颗有3种方案，3颗有1种方案，则解为LCM(1,3,3,1)=3

刚开始拿到这题的时候，和往常一样，找规律，于是开始列了一堆的计算结果

                                               LCM
1                                               1
1 1                                            1
1 2 1                                          2
1 3 3 1                                       3
1 4 6 4 1                                    12
1 5 10 10 5 1                               10
1 6 15 20 15 6 1                            60
1 7 21 35 35 21 7 1                       105
1 8 28 56 70 56 28 8 1                   280
1 9 36 84 126 126 84 36 9 1             252

然而并没有我要的规律，看了出题人的解题报告，我才知道居然有这样一个等价式

然而，出题人却没有对这个等价式进行证明，怎么想也想不通，这是如何得到的，本打算在这里做一个证明，但是，唉，个人水平有限，只能委屈大家点个链接了

知道这个式子之后，我们要求的就转化成了求LCM(1,2,…,n)了，这个的求法在出题人的报告里有介绍，当n是素数p的k次方时，LCM(1,2,…,n)=LCM(1,2,…,n-1)*p的，否则LCM(1,2,…,n)=LCM(1,2,…,n-1)，这个还是比较方便的，先打个素数表，然后将素数的k次方做个标记就可以了，然后再遍历一遍求f(n)=LCM(1,2,…,n)的值，剩下的就是取模工作了

因为f(n+1)/(n+1)是一个除法，而取模运算又是不满足除法的，没办法，看到一些人用了快速幂来求，就有样学样的拿来用了，可是不理解为什么快速幂的时候要mod-2，这个希望有人能帮我解答吧，毕竟相互学习嘛，而乘法逆元，同样也可以点个链接看看

好啦，放个代码，有问题的，我们来讨论讨论，共勉

#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<stdlib.h>
#include<cmath>
#include<string>
#include<algorithm>
#include<iostream>
#define exp 1e-10
using namespace std;
const int N = 1000002;
const int inf = 1000000000;
const int mod = 1000000007;
__int64 f[N],x;
int p[80000],k=0,s[N];
bool v[N];
void get_prime()//素数表
{
    memset(v,false,sizeof(v));
    for(int i=2;i<N;i++)
        if(!v[i])
        {
            p[k++]=i;
            for(int j=i*2;j<N;j+=i)
                v[j]=true;
        }
}
__int64 Quick_Mod(int a,int b)//快速幂
{
    __int64 res = 1,term = a % mod;
    while(b)
    {
        if(b & 1) res = (res * term) % mod;
        term = (term * term) % mod;
        b >>= 1;
    }
    return res;
}
int main()
{
    int t,n,i;
    get_prime();
    memset(v,false,sizeof(v));
    for(i=0;i<k;i++)
    {
        x=p[i];
        while(x<N)//将素数p的k次方p^k标记一下，方便计算f(n)
        {
            v[x]=true;
            s[x]=p[i];
            x*=p[i];
        }
    }
    f[1]=1;
    for(i=2;i<N;i++)//计算f(n)
        if(v[i])
            f[i]=(f[i-1]*s[i])%mod;//f(n)=f(n-1)*p
        else
            f[i]=f[i-1];//f(n)=f(n-1)
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d",&n);
        printf("%d\n",(f[n+1]*Quick_Mod(n+1,mod-2))%mod);//计算(f(n+1)/(n+1))%mod
    }
    return 0;
}

菜鸟成长记