解7月4号的那道题,计算迷宫中可行路径的条数
好长时间没写了,瞎忙活了两个来月,一直没什么心思继续下去,今天下午把之前的那道题想了想,挺简单的方法,直接用递归就可以了.用递归可以算出总数,并且可以输出可能的路径。但是效率不佳,由于可能的数据量庞大的情况下,数据量就会很大,这样效率就会不佳,最好用动态规划的方法来求解,按照反写的L的顺序计算出每个点的可能的条数,然后一个层的反写L按照上一层的反写的L计算,每一层反写L交点处的可能路径数在当层L中最后一个计算。
坐标系从(0,0)点走到(9,9)点,只能向右或者向上走,其中有些点不能走,问有多少种走法?
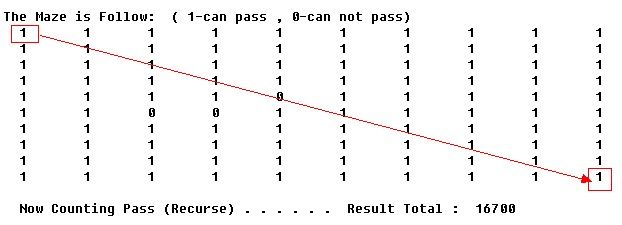
如图:假如。的位置不能走。(希望图能分辨清,左下角是(0,0))
..........
..........
..........
..。。......
....。.....
..........
..........
..........
..........
..........
/******************************************************************* * * DESCRIPTION: This programming is for counting the path number * from (0, 0) to (9, 9) in Maze * * AUTHOR: NeeSky * * DATE:2009-9-6 * *******************************************************************/ /*Macro Define*/ #define MaxSize 4 /*Include Files*/ #include <iostream> #include <ostream> /*Using Namespace */ using namespace std; /*Global Definition*/ char Maze[MaxSize][MaxSize]={ /*The Maze*/ {'1', '1', '1', '1'} , {'1', '0', '1', '1'} , {'1', '1', '0', '1'} , {'1', '1', '1', '1'}}; char Path[MaxSize][MaxSize]={ /*The Path Buffer*/ {'1', '1', '1', '1'} , {'1', '0', '1', '1'} , {'1', '1', '0', '1'} , {'1', '1', '1', '1'}}; int PathCount=0; /*The final Result of How many paths*/ /** * Output the Maze to ostream * */ void OutputMatrix(ostream &os, char Matrix[MaxSize][MaxSize]) { os<<endl; for(int i=0; i<MaxSize; ++i) { os<<" "; for(int j=0; j<MaxSize; ++j) os<<" "<<Matrix[i][j]<<" "; os<<endl; } return; } /** * Recursive Functions to Find Path Counting * And Display the Path * */ int GetPathCounting(int xStart, int yStart, int xEnd, int yEnd) { Path[xStart][yStart]='2'; if(((xStart==xEnd)&&(yStart==yEnd-1))||((yStart==yEnd)&&(xStart==xEnd-1))) { Path[xEnd][yEnd]='2'; OutputMatrix(cout, Path); Path[xEnd][yEnd]='1'; Path[xStart][yStart]='1'; return 1; /*Exit of Recursive*/ } if(Maze[xStart][yStart+1]=='1') /*Up Path*/ { PathCount+=GetPathCounting(xStart, yStart+1, xEnd, yEnd); } if(Maze[xStart+1][yStart]=='1')/*Right Path*/ { PathCount+= GetPathCounting(xStart+1, yStart, xEnd, yEnd); } Path[xStart][yStart]='1'; return 0;/*Very Important*/ } /** * Just Call the GetPathCounting Function and * GetPathCountingWithMath Function. * */ void ResolvePathCounting(void) { cout<<" The Maze is Follow: ( 1-can pass , 0-can not pass) "<<endl; OutputMatrix(cout, Maze); cout<<"/n Now Counting Pass (Recurse) [ 2 means FootPrint ] . . . . . ./n "; GetPathCounting(0,0,3,3); cout<<" Result Total : "<<PathCount<<endl; return; } /** *The Main Programming * * @author NeeSky (2009-9-6) * * @return int if Successful */ int main(void) { ResolvePathCounting(); return 0; }
输出:
以下为原题中的测试数据Maze[10][10],可能的路径太多,只求出总数,多达16700条路径