手机对话中的语音处理（二）

本系列文章由 @YhL_Leo 出品，转载请注明出处。
文章链接： http://blog.csdn.net/yhl_leo/article/details/50349856

本文就上一篇博客：手机对话中的语音处理（一）中讲述的LP分析合成算法，利用Matlab予以分析和验证。

验证试验的语音数据具有相同的采样位数，采样率，比特率（分别为16bit，8kHz，128kbps），已经上传到百度云盘（密码：h4do），需要可以自行下载。

图 1 测试语音数据

2 Matlab语音分析

以分享的语音文件h_orig为例（这段语音被加入了白噪声），在Matlab中打开查看其声波波形如图 2。

[speech,fs,bits] = wavread('h_orig.wav');
plot(speech);
xlabel('Time(samples)');
ylabel('Amplitude');

图 2 声波波形

图 3 语音文件参数

从图 3中可以看出，这个语音文件共有32000个采样点（浮点数），采样频率8000Hz，采样位数16bit，时长4s（32000samples / 8000(samples ⋅ s −1 ），如果你听了这段语音，就会发现这其实是一个男性说的一句英语。当让从图上根本看不出来说的内容是什么…

我们利用Hamming加权窗将语音帧定为50毫秒长（400samples），绘制出其对应的宽频频谱图（wideband spectrogram ），见图 4。

spectrogram(speech, 400, 360, 400, fs);

图 4 声波频谱图

从图 4中可看出，这段复杂的语音，在垂直方向，在100Hz~500Hz直接，有几条明显的红线，这就是语音的几个基频，虽然准确的频率不清楚，但是在有些应用中一些语音分析专家确实可以根据这些频谱读出其中的含义。（需要补充的一点：并不是所有的频谱都能够在同一参数下得到正确的结果的，Hamming窗大小这个参数对于频谱的显示有着重要的作用，当窗的长度或者数值较大时，时间轴方面的分辨率会比较差，具体体现在代表基频的红线会出现重叠的现象，比如上图。而当窗的长度或者数值较小时，红线在时间轴方向的重叠会大大减小，但是红线会在频率轴上展宽，给读取正确的频率值带来困难。）

2.1 30毫秒有声语音的LP合成

从图 2所示的波形图中，我们随意选出一段有声语音片段，这里选择第5000~5239个采样值：

input_frame=speech(5000:5239); plot(input_frame);

图 5 截取一段30毫秒的语音信号

可以看出，这段语音有一个近似的周期（大约为60个采样信号），当然细看的话，每个周期确实是不同的，这与实际是相符的，即基本不会出现相同的语音帧。

将上述的信号的频谱图绘制出（使用periodogram函数，点数设置为512，使用归一化频率，因此 π = Fs/2 ，当然这就就是4000Hz）。

periodogram(input_frame, [], 512);

图 6 功率谱密度图

从图 6中可以看出，其基频 F0 约为160Hz(0.4 ⋅ 4000Hz)，主要的共振峰主要有三个，所处的频率分别为400，1200和2500Hz（这里的解均是估算，不一定准确）。

接着，使用LP模型（令 p=10 ）来拟合上述的频谱。同时解得预测系数 {ai} 和残差的方差 σ :

[ai, sigma_square] = lpc(input_frame, 10);
sigma = sqrt(sigma_square);

前一篇博客已经提到，估算LP参数的方法是Levinson–Durbin算法，求解的预测参数使得预测的残差值具有最小均方和。不多说，上代码和图：

[HI, WI] = freqz(ai,1, 512);
[H, W] = freqz(1, ai, 512);
plot(W, 20*log10(abs(H)), '-', WI, 20*log10(abs(HI)), '--');
legend('Systhsis filter 1/A(z)', 'Inverse filter A(z)');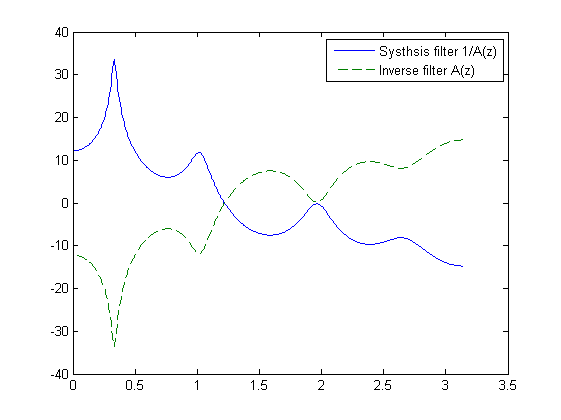

图 7 合成滤波和逆滤波的频率响应曲线

从图 6和图 7能发现什么，没错，后者就像是前者的一个平滑简化结果，如果将这两个图在一张图里显示，就可以看到后者与前者的频率包络基本匹配，见图 8。

periodogram(input_frame, [], 512, 2);
hold on 
plot(W/pi, 20*log10(sigma*abs(H)), 'r-');
hold off
legend('Original frequency', 'Systhsis filter 1/A(z)');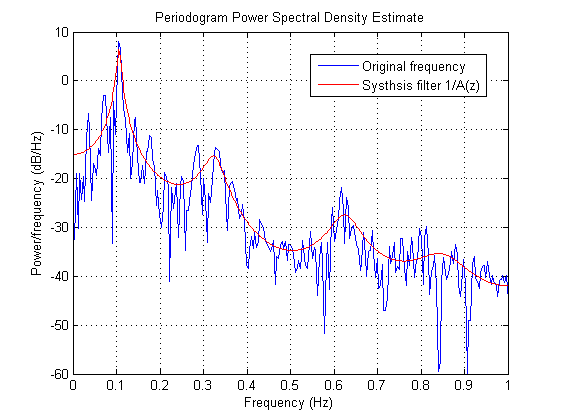

图 8 合成滤波的频率响应曲线和语音帧的频谱图叠加

我们将 {ai} 的零极点图，展示在图 9中，可以看出有1个零点，10个极点，且极点全都位于单位元内，一定程度上呈现出均匀分布。换句话说，LPC拟合可以自动地调整合成滤波的极点，并且贴近单位圆周圆周，使得拟合曲线尽可能地模仿原频谱共振峰响应曲线。

zplane(1, ai);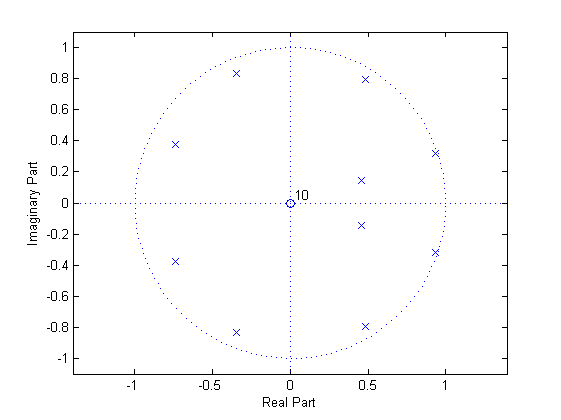

图 9 合成滤波的零极点图

将估算的参数作用在输入语音帧中，我们就可以获得预测残差：

LP_residual = filter(ai, 1, input_frame); plot(LP_residual); periodogram(LP_residual, [], 512);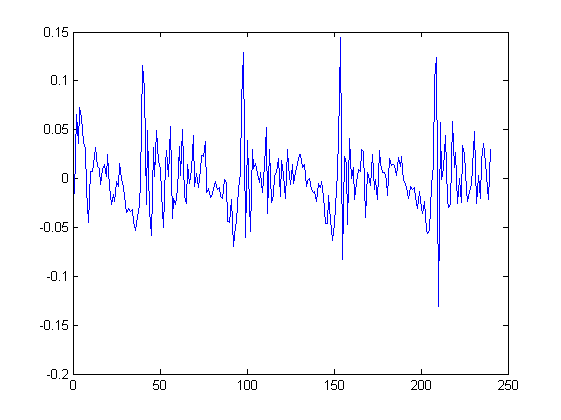

图 10 LP预测残差图

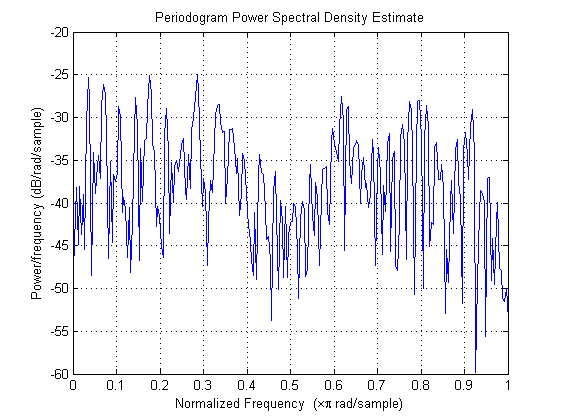
图 11 LP预测残差功率谱密度图

从图 10 中可以看出，残差基本在0附近摆动，而从图 11中可以看出其频谱图相对于原始信号的频谱图（见图 6）基本接近平稳，而且具有更多良好的细节，尤其是可以看到频谱的基频和谐频部分都被很好得保留下来。

当然，如果我们将合成滤波作用于预测残差就可以得到原分析语音（合成滤波可以看出是逆滤波的逆变换），与原信号无异，见图 12。

output_frame = filter(1, ai, LP_residual); plot(output_frame);

图 12

LPC模型可以通过利用一组可调的基频周期和振幅的脉冲序列，模仿有声语音的预测残差。针对上述的语音帧，较好的选择可以是间隔64个采样信号为0的激励脉冲序列，另外为了让方差与残差信号相匹配，还需要给激励信号乘上一个增益值。

excitation = [1;zeros(64,1);1;zeros(64,1);1;zeros(64,1);1;zeros(44,1)];
gain = sigma/sqrt(1/65);
plot(gain*excitation);
periodogram(gain*excitation, [], 512);

图 13 激励脉冲

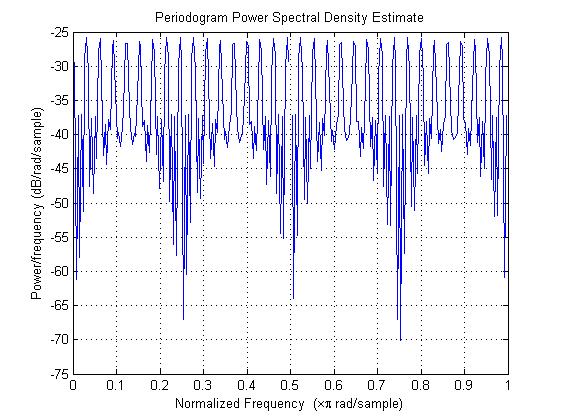
图 14 激励脉冲功率谱密度图

图 13所示的激励脉冲很像采样函数，只不过相对于原始信号采样频率小得多而已。而且从波形上看，它跟图10 所示的预测残差图有些相似（在相同的位置具有较大峰值，其他位置很，趋势相似），不过主要的区别在于激励频谱有点“over-harmonic”。

前面铺垫了那么多，都是再为语音合成做准备，让门来最终见识一下LP合成滤波器产生语音的效果吧：

synt_frame = filter(gain, ai, excitation); plot(synt_frame); periodogram(synt_frame, [], 512);

图 15 合成语音波形图

图 16 合成语音功率谱密度图

是的，这就是折腾了一圈以后合成的语音，与图 5和图 6比较，可以发现两者的语音波形明显并不相同（这是因为LP算法并不考虑原始语音波谱的相位），但是可以看出两者的频谱包络却比较相似，然而细看你又会发现在谐频的细节上两者也是有较大的差别。你可以将合成的语音播放出来：

sound(synt_frame, fs );

当然，由于时间太短（30毫秒），你可能只听到响了一声就没了，与input_frame对比好像也听不出区别…

这就是有声语音合成的LP算法应用，回忆在上篇博客中所述的：LP模型的本意只是获得原语音信号的波谱包络特征，而不是最大程度模仿整个语音波型，你会发现最终获得的合成语音也是满足这样的规律，从语音波形上合成结果并不让人满意，但是其频谱包络特征却与原始信号具有一致性。