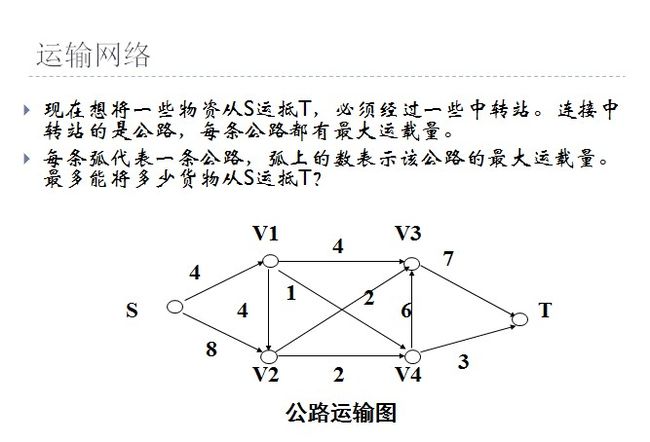
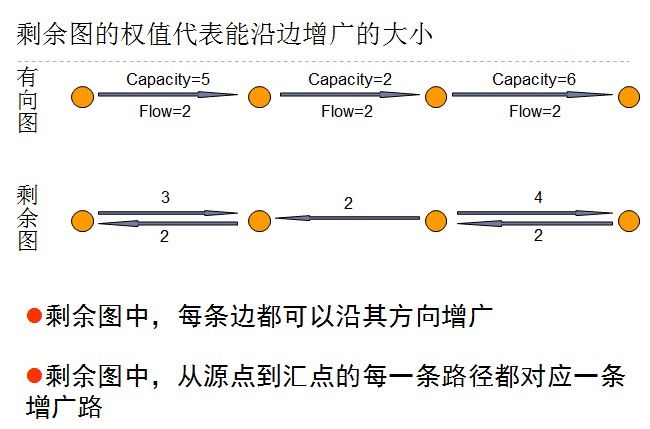
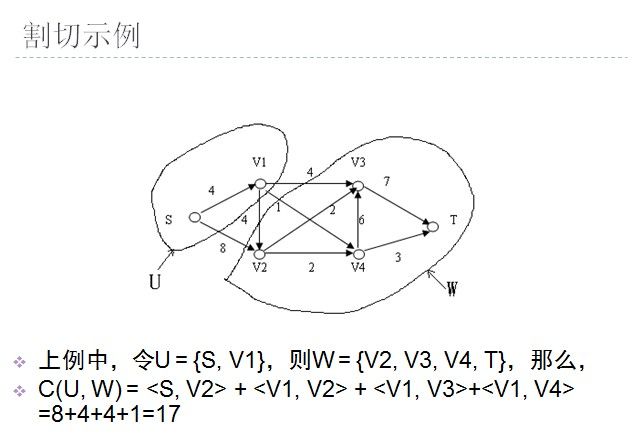
poj 1087 我们一起学习网络流吧
最近一直想搞定这道题目。看了discuss才知道是网络流的题目,好多人说可以用二分图匹配做,这个还没想明白,还是看看经典的网络流吧。以前学习过相关的知识,但是由于学习的时间比较久,加上当时也是学的马马虎虎,所以导致现在对网络流完全不理解。这段时间,抽时间看了一些网上的资料,加上算法导论上的一些解释,也算整明白了。不敢独享,在这里晒晒自己学到的东西,分享。。。
网络流基础知识:
本程序用的就是Dinic算法,这里介绍一下Dinic算法
伪代码表示:
下面是伪代码的具体代码:
// max net stream
#include <cstdio>
#include <cstring>
#include <map>
#include <string>
#include <vector>
#include <iostream>
using namespace std;
map<string, int>mp;
vector<int>G[800];//无向图
int n, m, k;
int que[800];
int d[800];
int stack[800];
int g[800][800];//有向流网络
bool v[800];
//寻找增广层次路径
bool Bfs(int s, int t)
{
int l = 0;
int r = 0;
int i, p;
memset(d, -1, sizeof(d));
d[s] = 0;
que[r ++] = s;
while (l < r)
{
p = que[l ++];
for (i = 0; i < G[p].size(); ++ i)
{
int u = G[p][i];
if (g[p][u] > 0 && d[u] == -1)
{
d[u] = d[p] + 1;//增广最短路
if (u == t)
{
return true;
}
que[r ++ ] = u;
}
}
}
return false;
}
int Dinic_Maxflow(int s, int t)
{
int i , p;
int nMinc;
int minn;
int ans = 0;
// 找增广路径,直到找不到为止
while (Bfs(s, t))
{
int top = 0, base = 0;
memset(v, false, sizeof(v));
stack[top ++] =s;
v[s] = true;
while (top > base)
{
p = stack[top - 1];
if (p == t)//找到一条
{
minn = 0xfffffff;
for(i = 1; i < top; ++ i)//求出增广路上的最小值
{
int u = stack[i - 1];
int v = stack[i];
if (g[u][v] < minn)
{
minn = g[u][v];
nMinc = u;
}
}
ans += minn;//增加流量
for (i = 1; i < top; ++ i)//更新增广路
{
int u = stack[i - 1];
int v = stack[i];
g[u][v] -= minn;
g[v][u] += minn;
}
while (top > base && stack[top - 1] != nMinc)//重新回到标号点,一次标号,多次增广
{
top --;
}
}
else//找到增广路
{
for (i = 0; i < G[p].size(); ++ i)
{
int u = G[p][i];
if (! v[u] && g[p][u] > 0 && d[u] == d[p] + 1)
{
v[u] = true;
stack[top ++] = u;
break;
}
}
if (i == G[p].size())
{
top --;
}
}
}
}
return ans;
}
int main()
{
int index;
int tot;
char str[30],ss[30];
while (scanf("%d", &n) != EOF)
{
index = 1;
mp.clear();
memset(g, 0 ,sizeof(g));
memset(G, 0, sizeof(G));
//插座和汇点连接
while (n --)
{
scanf("%s", str);
mp[str] = index ++;
G[mp[str]].push_back(799);
g[mp[str]][799] = 1;
}
scanf("%d", &m);
tot = m;
//设备和源点连接
while (m --)
{
scanf("%s%s", ss, str);
mp[ss] = index ++;
g[0][mp[ss]] = 1;
if (! mp[str])
{
mp[str] = index ++;
}
G[0].push_back(mp[ss]);
G[mp[ss]].push_back(mp[str]);
G[mp[str]].push_back(mp[ss]);
g[mp[ss]][mp[str]] = 1;
}
scanf("%d", &k);
//转接点
while (k --)
{
scanf("%s%s", ss, str);
if (! mp[str])
{
mp[str] = index ++;
}
G[mp[ss]].push_back(mp[str]);
G[mp[str]].push_back(mp[ss]);
g[mp[ss]][mp[str]] = 0xfffffff;
}
printf("%d\n", tot - Dinic_Maxflow(0, 799));
}
return 0;
}
这里主要做两点解释吧,估计也是很多人不明白的地方
1、为何找到一条增广路径中的最小值时,正向减去这个值,反向加上这个值。
在这幅图中我们首先要增广1->2->4->6,这时可以获得一个容量为2的流,但是如果不建立4->2反向弧的话,则无法进一步增广,最终答案为2,显然是不对的,然而如果建立了反向弧4->2,则第二次能进行1->3->4->2->5->6的增广,最大流为3.
Comzyh对反向弧的理解可以说是"偷梁换柱",请仔细阅读:在上面的例子中,我们可以看出,最终结果是1->2->5->6和1->2->4->6和1->3->4->6.当增广完1->2->4->5(代号A)后,在增广1->3->4->2->5->6(代号B),相当于将经过节点2的A流从中截流1(总共是2)走2->5>6,而不走2->4>6了,同时B流也从节点4截流出1(总共是1)走4->6而不是4->2->5->6,相当于AB流做加法.
简单的说反向弧为今后提供反悔的机会,让前面不走这条路而走别的路.
2、为何找到一条以后,退到最小值那个点
这就是为了提高效率,减少不必要的搜索。也就是当我们找到一条最短的路径的时候,可以一次搜索,多次增广,一直到这条不能增广为止。然后再去寻找下一条。
比如有1---8个点构成的图。 1-4-5-6-7-8是最短的,而5-6是最短的。下一个是6-7,如果继续搜索,那就是搜完第一条,直接回搜到6-7了。否则我们可能在下一次,1-2-3-4-6-7-8这样就多了1 -2-3-4这些搜索。总之就是尽量将一条最短路上的增广找完。自己画画吧。。。。
不早了, gg, 睡觉。。。。。下次再细细学习。