十大经典矩阵
经典题目1 给定n个点,m个操作,构造O(m+n)的算法输出m个操作后各点的位置。操作有平移、缩放、翻转和旋转
这里的操作是对所有点同时进行的。其中翻转是以坐标轴为对称轴进行翻转(两种情况),旋转则以原点为中心。如果对每个点分别进行模拟,那么m个操作总共耗时O(mn)。利用矩阵乘法可以在O(m)的时间里把所有操作合并为一个矩阵,然后每个点与该矩阵相乘即可直接得出最终该点的位置,总共耗时O(m+n)。假设初始时某个点的坐标为x和y,下面5个矩阵可以分别对其进行平移、旋转、翻转和旋转操作。预先把所有m个操作所对应的矩阵全部乘起来,再乘以(x,y,1),即可一步得出最终点的位置。

经典题目2 给定矩阵A,请快速计算出A^n(n个A相乘)的结果,输出的每个数都mod p。
由于矩阵乘法具有结合律,因此A^4 = A * A * A * A = (A*A) * (A*A) = A^2 * A^2。我们可以得到这样的结论:当n为偶数时,A^n = A^(n/2) * A^(n/2);当n为奇数时,A^n = A^(n/2) * A^(n/2) * A (其中n/2取整)。这就告诉我们,计算A^n也可以使用二分快速求幂的方法。例如,为了算出A^25的值,我们只需要递归地计算出A^12、A^6、A^3的值即可。根据这里的一些结果,我们可以在计算过程中不断取模,避免高精度运算。
经典题目3 POJ3233(感谢rmq)
题目大意:给定矩阵A,求A + A^2 + A^3 + …+ A^k的结果(两个矩阵相加就是对应位置分别相加)。输出的数据mod m。k<=10^9。
这道题两次二分,相当经典。首先我们知道,A^i可以二分求出。然后我们需要对整个题目的数据规模k进行二分。比如,当k=6时,有:
A + A^2 + A^3 + A^4 + A^5 + A^6 =(A + A^2 + A^3)+ A^3*(A + A^2 + A^3)
应用这个式子后,规模k减小了一半。我们二分求出A^3后再递归地计算A + A^2 + A^3,即可得到原问题的答案。
经典题目4 VOJ1049
题目大意:顺次给出m个置换,反复使用这m个置换对初始序列进行操作,问k次置换后的序列。m<=10, k<2^31。
首先将这m个置换“合并”起来(算出这m个置换的乘积),然后接下来我们需要执行这个置换k/m次(取整,若有余数则剩下几步模拟即可)。注意任意一个置换都可以表示成矩阵的形式。例如,将1 2 3 4置换为3 1 2 4,相当于下面的矩阵乘法:
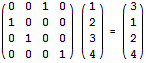
置换k/m次就相当于在前面乘以k/m个这样的矩阵。我们可以二分计算出该矩阵的k/m次方,再乘以初始序列即可。做出来了别忙着高兴,得意之时就是你灭亡之日,别忘了最后可能还有几个置换需要模拟。
经典题目5 《算法艺术与信息学竞赛》207页(2.1代数方法和模型,[例题5]细菌,版次不同可能页码有偏差)
大家自己去看看吧,书上讲得很详细。解题方法和上一题类似,都是用矩阵来表示操作,然后二分求最终状态。
经典题目6 给定n和p,求第n个Fibonacci数mod p的值,n不超过2^31
根据前面的一些思路,现在我们需要构造一个2 x 2的矩阵,使得它乘以(a,b)得到的结果是(b,a+b)。每多乘一次这个矩阵,这两个数就会多迭代一次。那么,我们把这个2 x 2的矩阵自乘n次,再乘以(0,1)就可以得到第n个Fibonacci数了。不用多想,这个2 x 2的矩阵很容易构造出来:
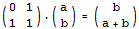
经典题目7 VOJ1067
我们可以用上面的方法二分求出任何一个线性递推式的第n项,其对应矩阵的构造方法为:在右上角的(n-1)*(n-1)的小矩阵中的主对角线上填1,矩阵第n行填对应的系数,其它地方都填0。例如,我们可以用下面的矩阵乘法来二分计算f(n) = 4f(n-1) - 3f(n-2) + 2f(n-4)的第k项:
利用矩阵乘法求解线性递推关系的题目我能编出一卡车来。这里给出的例题是系数全为1的情况。
经典题目8 给定一个有向图,问从A点恰好走k步(允许重复经过边)到达B点的方案数mod p的值
把给定的图转为邻接矩阵,即A(i,j)=1当且仅当存在一条边i->j。令C=A*A,那么C(i,j)=ΣA(i,k)*A(k,j),实际上就等于从点i到点j恰好经过2条边的路径数(枚举k为中转点)。类似地,C*A的第i行第j列就表示从i到j经过3条边的路径数。同理,如果要求经过k步的路径数,我们只需要二分求出A^k即可。
这里的操作是对所有点同时进行的。其中翻转是以坐标轴为对称轴进行翻转(两种情况),旋转则以原点为中心。如果对每个点分别进行模拟,那么m个操作总共耗时O(mn)。利用矩阵乘法可以在O(m)的时间里把所有操作合并为一个矩阵,然后每个点与该矩阵相乘即可直接得出最终该点的位置,总共耗时O(m+n)。假设初始时某个点的坐标为x和y,下面5个矩阵可以分别对其进行平移、旋转、翻转和旋转操作。预先把所有m个操作所对应的矩阵全部乘起来,再乘以(x,y,1),即可一步得出最终点的位置。

经典题目2 给定矩阵A,请快速计算出A^n(n个A相乘)的结果,输出的每个数都mod p。
由于矩阵乘法具有结合律,因此A^4 = A * A * A * A = (A*A) * (A*A) = A^2 * A^2。我们可以得到这样的结论:当n为偶数时,A^n = A^(n/2) * A^(n/2);当n为奇数时,A^n = A^(n/2) * A^(n/2) * A (其中n/2取整)。这就告诉我们,计算A^n也可以使用二分快速求幂的方法。例如,为了算出A^25的值,我们只需要递归地计算出A^12、A^6、A^3的值即可。根据这里的一些结果,我们可以在计算过程中不断取模,避免高精度运算。
经典题目3 POJ3233(感谢rmq)
题目大意:给定矩阵A,求A + A^2 + A^3 + …+ A^k的结果(两个矩阵相加就是对应位置分别相加)。输出的数据mod m。k<=10^9。
这道题两次二分,相当经典。首先我们知道,A^i可以二分求出。然后我们需要对整个题目的数据规模k进行二分。比如,当k=6时,有:
A + A^2 + A^3 + A^4 + A^5 + A^6 =(A + A^2 + A^3)+ A^3*(A + A^2 + A^3)
应用这个式子后,规模k减小了一半。我们二分求出A^3后再递归地计算A + A^2 + A^3,即可得到原问题的答案。
经典题目4 VOJ1049
题目大意:顺次给出m个置换,反复使用这m个置换对初始序列进行操作,问k次置换后的序列。m<=10, k<2^31。
首先将这m个置换“合并”起来(算出这m个置换的乘积),然后接下来我们需要执行这个置换k/m次(取整,若有余数则剩下几步模拟即可)。注意任意一个置换都可以表示成矩阵的形式。例如,将1 2 3 4置换为3 1 2 4,相当于下面的矩阵乘法:
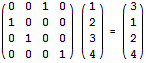
置换k/m次就相当于在前面乘以k/m个这样的矩阵。我们可以二分计算出该矩阵的k/m次方,再乘以初始序列即可。做出来了别忙着高兴,得意之时就是你灭亡之日,别忘了最后可能还有几个置换需要模拟。
经典题目5 《算法艺术与信息学竞赛》207页(2.1代数方法和模型,[例题5]细菌,版次不同可能页码有偏差)
大家自己去看看吧,书上讲得很详细。解题方法和上一题类似,都是用矩阵来表示操作,然后二分求最终状态。
经典题目6 给定n和p,求第n个Fibonacci数mod p的值,n不超过2^31
根据前面的一些思路,现在我们需要构造一个2 x 2的矩阵,使得它乘以(a,b)得到的结果是(b,a+b)。每多乘一次这个矩阵,这两个数就会多迭代一次。那么,我们把这个2 x 2的矩阵自乘n次,再乘以(0,1)就可以得到第n个Fibonacci数了。不用多想,这个2 x 2的矩阵很容易构造出来:
经典题目7 VOJ1067
我们可以用上面的方法二分求出任何一个线性递推式的第n项,其对应矩阵的构造方法为:在右上角的(n-1)*(n-1)的小矩阵中的主对角线上填1,矩阵第n行填对应的系数,其它地方都填0。例如,我们可以用下面的矩阵乘法来二分计算f(n) = 4f(n-1) - 3f(n-2) + 2f(n-4)的第k项:
利用矩阵乘法求解线性递推关系的题目我能编出一卡车来。这里给出的例题是系数全为1的情况。
经典题目8 给定一个有向图,问从A点恰好走k步(允许重复经过边)到达B点的方案数mod p的值
把给定的图转为邻接矩阵,即A(i,j)=1当且仅当存在一条边i->j。令C=A*A,那么C(i,j)=ΣA(i,k)*A(k,j),实际上就等于从点i到点j恰好经过2条边的路径数(枚举k为中转点)。类似地,C*A的第i行第j列就表示从i到j经过3条边的路径数。同理,如果要求经过k步的路径数,我们只需要二分求出A^k即可。
经典题目 9 用 1 x 2 的多米诺骨牌填满M x N的矩形有多少种方案,M<=5,N<2^31,输出
答案
,输出
答案mod p的结果
我们以M=3 为例进行讲解。假设我们把这个矩形横着放在电脑屏幕上,从右往左一
列地进行填充。其中前n-2 列已经填满了,第n-1 列参差不齐。现在我们要做的事情是把第
列也填满,将状态转移到第n列上去。由于第n-1 列的状态不一样(有 8 种不同的状态)
列一
n-1
,
我们需要分情况进行讨论。在图中,我把转移前 8 种不同的状态放在左边,转移后 8
因此
种不同的状态放在右边,左边的某种状态可以转移到右边的某种状态就在它们之间连一根
线。 注意为了保证方案不重复, 状态转移时我们不允许在第n-1 列竖着放一个多米诺骨牌 (例
如左边第 2 种状态不能转移到右边第 4 种状态) ,否则这将与另一种转移前的状态重复。把
这 8 种状态的转移关系画成一个有向图,那么问题就变成了这样:从状态 111 出发,恰好经
过n步回到这个状态有多少种方案。 比如, n=2 时有 3 种方案, 111->011->111、 111->110->111
和 111->000->111,这与用多米诺骨牌覆盖 3×2 矩形的方案一一对应。这样这个题目就转化
为了我们前面的例题 8。
后面我写了一份此题的源代码。你可以再次看到位运算的相关应用。
经典题目 10 POJ2778
题目大意是,检测所有可
的DNA只能由ACTG四个字符构成。题目将给出 10 个以内的病毒片段,
能的n位DNA串有多少个DNA串中不含有指定的病毒片段。合法
每个片段长度不超
过
下面的讲解中我们以
通过构图将问题转化为例题 8。我们找出所有病毒片段的前缀,把n位DNA分为以下 7 类:
以AT结尾、以AA结尾、以GG结尾、以?A结尾、以?G结尾、以?C结尾和以??结尾。其中问
号表示“其它情况”,它可以是任一字母,只要
缀。显然,这些分类是全集的一个划分(交集为空,并集为全集) 。现在,假如我们已经知
道了长度为n-1 的各类DNA中符合要求的DNA个数,我们需要求出长度为n时各类DNA的个
数。 我们可以根据各类型间的转移构造一个边上带权的有向图。 例如, 从AT不能转移到AA,
从AT转移到??有 4 种方法(后面加任一字母) ,从?A转移到AA有 1 种方案(后面加个A) ,
从?A转移到??有 2 种方案 (后面加G或C) , 从GG到??有 2 种方案 (后面加C将构成病毒片段,
不合法,只能加A和T)等等。这个图的构造过程类似于用有限状态自动机做串匹配。然后,
我们就把这个图转化成矩阵,让这个矩阵自乘n次即可。最后输出的是从??状态到所有其它
状态的路径数总和。
题目中的数据规模保证前缀数不超过 100,一次矩阵乘法是三方的,一共要乘log(n)次。
因此这题总的复杂度是 100^3 * log(n),AC了。
最后给出第 9 题的代码供大家参考(今天写的,熟
了避免大家看代码看着看着就忘了,我把这句话放在前面来说:
Matrix67 原创,转贴请注明出处。
#include <cstdio>
#define SIZE (1<<m)
#define MAX_SIZE 32
u
class CMatrix
{
public:
void s
CMat
CMatrix power(int);
private:
int size;
long modulo;
};
void CMatrix::setS
{
element[i][j]=0;
10。数据规模n<=2 000 000 000。
ATC,AAA,GGC,CT这四个病毒片段为例,说明怎样像上面的题一样
这个字母不会让它所在的串成为某个病毒的前
悉了一下C++的类和运算符重载) 。为
sing namespace std;
long element[MAX_SIZE][MAX_SIZE];
etSize(int);
void setModulo(int);
rix operator* (CMatrix);
ize(int a)
for (int i=0; i<a; i++)
for (int j=0; j<a; j++)
size = a;
}
void CMatrix::setModulo(int a
{
}
CM
{
product.setModulo(modulo);
for (int j=0;
for (int k=0; k
{
product.element
[j];
product.element[i][j]%=
}
r
}
C
{
else if (exp & 1) return tmp
}
int main()
{
CMatrix
scanf("%d%d%d", &n, &m, &p);
unit.setSize(S
for(int i=0; i
if( ((~i)&j) == ((~i)
)
modulo = a;
atrix CMatrix::operator* (CMatrix param)
CMatrix product;
product.setSize(size);
for (int i=0; i<size; i++)
j<size; j++)
<size; k++)
[i][j]+=element[i][k]*param.element[k]
modulo;
eturn product;
Matrix CMatrix::power(int exp)
CMatrix tmp = (*this) * (*this);
if (exp==1) return *this;
.power(exp/2) * (*this);
else return tmp.power(exp/2);
const int validSet[]={0,3,6,12,15,24,27,30};
long n, m, p;
unit;
IZE);
<SIZE; i++)
for(int j=0; j<SIZE; j++)
&(SIZE-1)) )
{
bool isValid=f
for
(i
k++)isValid=isValid||(i&j)==validSet[k];
}
unit.setModulo(p);
printf("%d", unit.power(n).element[SIZE-
return 0;
}
alse;
nt
k=0;
k<8;
unit.element[i][j]=isValid;
1][SIZE-1] );