前几天为了UVa的一道题不得不重写了一个最小树形图O(VE)的模板,原先的是邻接矩阵版,所以复杂度是O(V^3)的。我的计划就是学/复习一个算法就 写一个总结上来,最后能逐渐的把我的学习经历记录一下。当然把其中一些理解写出来的话也会更加的深刻,或许还能帮到某些人,不是么,呵呵。
最小树形图,就是给有向带权图中指定一个特殊的点v,求一棵有向生成树T,使得该有向树的根为v,并且T中所有边的总权值最小。最小树形图的第一个算法是1965年朱永津和刘振宏提出的复杂度为O(VE)的算法。
判断是否存在树形图的方法很简单,只需要以v为根作一次图的遍历就可以了,所以下面的算法中不再考虑树形图不存在的情况。
在所有操作开始之前,我们需要把图中所有的自环全都清除。很明显,自环是不可能在任何一个树形图上的。只有进行了这步操作,总算法复杂度才真正能保证是O(VE)。
首先为除根之外的每个点选定一条入边,这条入边一定要是所有入边中最小的。现在所有的最小入边都选择出来了,如果这个入边集不存在有向环的话,我们可以 证明这个集合就是该图的最小树形图。这个证明并不是很难。如果存在有向环的话,我们就要将这个有向环所称一个人工顶点,同时改变图中边的权。假设某点u在 该环上,并设这个环中指向u的边权是in[u],那么对于每条从u出发的边(u, i, w),在新图中连接(new, i, w)的边,其中new为新加的人工顶点; 对于每条进入u的边(i, u, w),在新图中建立边(i, new, w-in[u])的边。为什么入边的权要减去in[u],这个后面会解释,在这里先给出算法的步骤。然后可以证明,新图中最小树形图的权加上旧图中被收缩 的那个环的权和,就是原图中最小树形图的权。
上面结论也不做证明了。现在依据上面的结论,说明一下为什么出边的权不变,入边的权要减去in [u]。对于新图中的最小树形图T,设指向人工节点的边为e。将人工节点展开以后,e指向了一个环。假设原先e是指向u的,这个时候我们将环上指向u的边 in[u]删除,这样就得到了原图中的一个树形图。我们会发现,如果新图中e的权w'(e)是原图中e的权w(e)减去in[u]权的话,那么在我们删除 掉in[u],并且将e恢复为原图状态的时候,这个树形图的权仍然是新图树形图的权加环的权,而这个权值正是最小树形图的权值。所以在展开节点之后,我们 得到的仍然是最小树形图。逐步展开所有的人工节点,就会得到初始图的最小树形图了。
如果实现得很聪明的话,可以达到找最小入边O(E),找环 O(V),收缩O(E),其中在找环O(V)这里需要一点技巧。这样每次收缩的复杂度是O(E),然后最多会收缩几次呢?由于我们一开始已经拿掉了所有的 自环,我门可以知道每个环至少包含2个点,收缩成1个点之后,总点数减少了至少1。当整个图收缩到只有1个点的时候,最小树形图就不不用求了。所以我们最 多只会进行V-1次的收缩,所以总得复杂度自然是O(VE)了。由此可见,如果一开始不除去自环的话,理论复杂度会和自环的数目有关。
最小树形图的总结到此为止了。目前为止发现的有OJ可交的最小树形图总共有3道题,分别是UVa 11183 Teen Girl Squad , TJU 2248 Channel Design , PKU 3164 Command Network 。其中UVa的题V = 1000, E = 40000,PKU和TJU是V = 100, E = 10000。在PKU/TJU下,由于数据范围的限制,采用O(V^3)的邻接矩阵会比O(VE)的邻接表快,而UVa的题显然只能用O(VE)的树形图算法了。
Minimum Spanning Tree: Chu-Liu/Edmonds Algorithm
Chu-Liu/Edmonds Algorithm
Chu-Liu/Edmonds Algorithm 用來求出有向圖的其中一棵最小生成樹(或者最大生成樹)。
想法
一棵生成樹上每一個點,都僅有一條入邊(除了根以外)。要找生成樹,圖上每一個點,都必須找到一條入邊(但不會是自己連向自己的入邊)。
既然要找最小生成樹,當然就是找權重越小的邊越好囉。每一個點(除了根以外)各自找到權重最小的入邊之後,有可能就剛好是一棵最小生成樹了,但是也有可能形成幾隻水母。
水母(沒有正式名稱,因為像水母就把它叫做水母)
由於每個點都僅有一條入邊,如果形成環,環上一定只有出邊,不會有入邊。每個點都僅有一條入邊,除了剛好形成一棵樹以外,要不就是形成水母──一只環再加上環上的點各是一棵樹的樹根,或者說是很多棵樹的樹根用環串起。

水母與最小生成樹
最小生成樹不得有環,所以水母是不合格的。然而水母是權重最小的連接方式,若有一棵恰當的最小生成樹,其權重會稍高於水母。
一、改變水母環上的邊,讓水母變成一棵樹。儘管整體權重稍微變大,但仍可接受。
二、改變水母觸手上的邊,並沒有比較好。不但讓整體權重變大,而且水母環仍舊存在,並沒有解決掉不合格的問題。
得到結論:只需要嘗試打開水母環上的邊就行了。打開邊的時候,要同時考慮新連入的邊的權重,以及被取消的邊的權重。選擇差值最小者,可讓總權重增加最小。進入水母環的邊全部都看過一遍後,就能選出差值最小者。
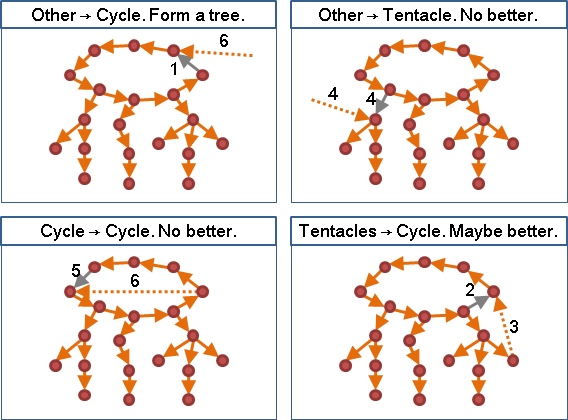
連入水母環的邊
根據 Kruskal's Algorithm 提到的最小生成樹相連性質,可以知道連接多隻水母,就和連接多棵最小生成樹的道理是一樣的,以權重小的邊來連接是最好的。唯一不同的是, Kruskal's Algorithm 一旦發現造成環的邊,就直接捨棄; Chu-Liu/Edmonds Algorithm 則是留下造成環的邊(形成水母),並且嘗試各種打開環的方式。
演算法
1. 刪去所有自己連向自己的入邊。
2. 重複以下步驟,直到形成生成樹為止:
甲、找出圖上每個點的最小入邊。O(E)
如果有兩個點以上找不到入邊,則表示生成樹不存在。
(找不到入邊的點可作為生成樹樹根)
乙、找出所有水母。如果沒有水母就表示目前已是最小生成樹。O(V)
丙、調整所有進入水母環的邊的權重。O(E)
w(a, x) -= w(å, x),åx是x點的最小入邊,ax為其他連入x點的邊。
丁、收縮水母環成為一點。O(E)
如果要固定樹根的話:
1. 刪去所有自己連向自己的入邊。
2. 移除樹根的全部入邊。
3. 判斷樹根能不能連到圖上各個點,否則生成樹不存在。
4. 重複以下步驟,直到形成生成樹為止:
甲、找出圖上每個點的最小入邊。O(E)
乙、找出所有水母。如果沒有水母就表示目前已是最小生成樹。O(V)
丙、調整所有進入水母環的邊的權重。O(E)
w(a, x) -= w(å, x),åx是x點的最小入邊,ax為其他連入x點的邊。
丁、收縮水母環成為一點。O(E)
最糟的情況是每個步驟中剛好產生一直水母環有兩個點的水母,水母環進行收縮後,整張圖只減少一個點。所以最多要進行 V-1 次步驟,總共的時間複雜度會是 O(V*E) 。
據說此演算法還可以加速成 O(V^2) 以及 O(ElogV) ,不過我不知道怎麼做就是了。
固定樹根:找出一棵最小生成樹+計算最小生成樹權重(簡單的資料結構)
- int V, E;
- struct Edge { int a, b, c;} Ed[40000];
- int d[1000], p[1000], v[1000], n[1000], m[1000];
-
-
-
- int MST( int r)
- {
- memset(m, 0, sizeof (m));
-
-
- int w1 = 0, w2 = 0;
- while ( true )
- {
-
-
-
-
-
- memset(d, 1, sizeof (d));
- memset(p, -1, sizeof (p));
-
- for ( int i=0; i<E; ++i)
- {
- int &a = Ed[i].a, &b = Ed[i].b, &c = Ed[i].c;
- if (a != b && b != r && c < d[b])
- d[b] = c, p[b] = a;
- }
-
-
-
-
-
-
-
-
- memset(v, -1, sizeof (v));
- memset(n, -1, sizeof (n));
-
- w1 = 0;
- bool jf = false ;
- for ( int i=0; i<V; ++i)
- {
- if (m[i]) continue ;
- if (p[i] == -1 && i != r) return 1e9;
- if (p[i] >= 0) w1 += d[i];
-
-
- int s;
- for (s = i; s != -1 && v[s] == -1; s = p[s])
- v[s] = i;
-
-
- if (s != -1 && v[s] == i)
- {
- jf = true ;
- int j = s;
- do
- {
- n[j] = s; m[j] = 1;
- w2 += d[j]; j = p[j];
-
- } while (j != s);
- m[s] = 0;
- }
- }
- if (!jf) break ;
-
-
-
-
-
-
- for ( int i=0; i<E; ++i)
- {
- int &a = Ed[i].a, &b = Ed[i].b, &c = Ed[i].c;
- if (n[b] >= 0) c -= d[b];
- if (n[a] >= 0) a = n[a];
- if (n[b] >= 0) b = n[b];
- if (a == b) Ed[i--] = Ed[--E];
- }
- }
- return w1 + w2;
- }
int V, E; struct Edge {int a, b, c;} Ed[40000]; int d[1000], p[1000], v[1000], n[1000], m[1000]; // 每個點最小入邊的權重,每個點最小入邊的來源, // 拜訪過,水母環,已收縮。 int MST(int r) { memset(m, 0, sizeof(m)); // 目前生成樹的權重,累計收縮水母環而失去的權重。 int w1 = 0, w2 = 0; while (true) // 一旦形成生成樹就停止。最多執行V-1次。 { /* O(E) graph traversal. find minimum in-edge for each vertice. --->o */ memset(d, 1, sizeof(d)); memset(p, -1, sizeof(p)); for (int i=0; i<E; ++i) { int &a = Ed[i].a, &b = Ed[i].b, &c = Ed[i].c; if (a != b && b != r && c < d[b]) d[b] = c, p[b] = a; } /* O(V) jellyfish detection ___ / / /___/ _/|||/_ //1// */ memset(v, -1, sizeof(v)); memset(n, -1, sizeof(n)); w1 = 0; bool jf = false; for (int i=0; i<V; ++i) { if (m[i]) continue; if (p[i] == -1 && i != r) return 1e9; if (p[i] >= 0) w1 += d[i]; // 找水母環 int s; for (s = i; s != -1 && v[s] == -1; s = p[s]) v[s] = i; // 標記水母環上的點,以及將會被收縮掉的點。 if (s != -1 && v[s] == i) { jf = true; int j = s; do { n[j] = s; m[j] = 1; w2 += d[j]; j = p[j]; } while (j != s); m[s] = 0; } } if (!jf) break; /* O(E) edge reweighting and cycle contraction ___ / / <- /___/ */ for (int i=0; i<E; ++i) { int &a = Ed[i].a, &b = Ed[i].b, &c = Ed[i].c; if (n[b] >= 0) c -= d[b]; if (n[a] >= 0) a = n[a]; if (n[b] >= 0) b = n[b]; if (a == b) Ed[i--] = Ed[--E]; } } return w1 + w2; }
UVa 11183
注:http://www.csie.ntnu.edu.tw/~u91029/SpanningTree.html

