背包问题C++程序

背包问题也是个很古老的问题了：

给一个一定容量的背包，有一定数量的物品，物品有重量和价值，如何装如这些物品，才使得装进背包里面的价值最高。

打劫珠宝店用得上的知识啊，呵呵。匪徒如何装走最大价值的东西呢？

设背包的容量是capacity， 用一个数据结构代表一个物品的重量和价值如下：

struct Jewel
{
	int w;
	int v;
	Jewel():w(0), v(0){}
	Jewel(int c, int d):w(c), v(d){}
};

然后用 vector<Jewel> &twoiv 代表现有的珠宝。vector<int> &vfill是记录什么东西是装了的。

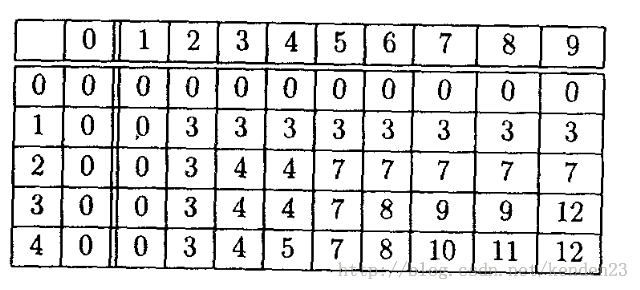
如下图填表，要诀就是：

比较难头脑转弯的就是要把列数看做是背包的总重量，一个单位重量一个单位重量地去填表。

逐行填入，有上到下，第一行和第一列都是0，因为没有东西装进；第二行是又左到右填入，每一格与上面和左边的格子的数字比较，大的填入这一格，然后把这一格的值和另外一个值比较，另外一个值是由当前背包容量（就是列的值，比如是第j列，那么当前装了j背包容量）减去要装入的物品的重量w，然后取得j-w值，查找这j-w列的值，加上当前需要填入的物品的价值v。这个的当前值和另外一个值，那个大就填入那个。

仔细看看这个图，从上到下，从左到右看。列是代表背包的总重量的，这个表的总重量是9.行是代表要填入的珠宝的序列号，从第一，到第四个珠宝一件一件地装入。

C++程序：

int knapSack(int &capacity, vector<Jewel> &twoiv , vector<int> &vfill)
{
	vector<vector<int> > vvi;
	vector<int> tempv(capacity+1, 0);
	for (int i = 0; i < twoiv.size()+1; i++)
	{
		vvi.push_back(tempv);
	}
	
	int i = 1;
	int j = 1;
	for (i = 1; i < twoiv.size() + 1; i++)
	{
		for (j = 1; j < capacity + 1; j++)
		{
			vvi[i][j] = max(vvi[i-1][j],vvi[i][j-1]);
			if (j - twoiv[i-1].w >= 0)
			{
				vvi[i][j] = max(vvi[i][j], vvi[i-1][j-twoiv[i-1].w] + twoiv[i-1].v);
			}
		}
	}

	vfill.resize(twoiv.size());
	for (int k = twoiv.size(), r = capacity; k > 0; k--)
	{
		if(vvi[k][r] > vvi[k-1][r])
		{
			vfill[k-1] = 1;
			r -= twoiv[k-1].w;
		}
		else vfill[k-1] = 0;
	}
	//注意：i,j已经超出了size（）和capacity了，所以需要-1
	return vvi[i-1][j-1];
}

vfill是从最后一行往上推才可以，它的容量是物品数量的容量。

基本思想是：

如果当前格的值比上一行的值大，那么就代表这一行的物品被装进来了。这个时候就需要置1。然后当前列代表的是背包容量，所以要减去该行物品的重量，以得到装入当前物品钱的背包前的重量。

测试程序如下：

int main()
{
	vector<Jewel> twoiv;
	int cap = 10;
	Jewel wv(2,6);
	twoiv.push_back(wv);
	wv.w = 2; wv.v = 3;
	twoiv.push_back(wv);
	wv.w = 6; wv.v = 5;
	twoiv.push_back(wv);
	wv.w = 5; wv.v = 4;
	twoiv.push_back(wv);
	wv.w = 4; wv.v = 6;
	twoiv.push_back(wv);
	vector<int> vfill;
	
	int most = knapSack(cap, twoiv, vfill);
	cout<<"The total value we can fill in is:"<<endl;
	cout<<most<<endl<<endl;

	cout<<"The jewels we pack in is:"<<endl;
	cout<<"indice: (weight,value)\n";
	for (int i = 0; i < vfill.size(); i++)
	{
		if(vfill[i] == 1)
			cout<<i<<":\t("<<twoiv[i].w<<",\t"<<twoiv[i].v<<")"<<endl;
	}
	
	system("pause");
	return 0;
}

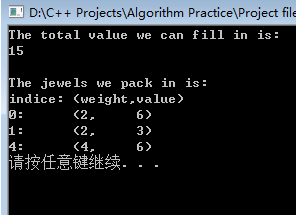
运行结果：