15.有序表查找与线索索引查找
转载请表明出处:http://blog.csdn.net/u012637501
一、有序表查找
1.折半查找/二分查找算法
(1)基本思想:在顺序存储的有序表中,取中间纪录(a[mid]=key)作为比较对象,若给定值与中间纪录的关键字相等,则查找成功;若给定值小于中间纪录的关键字,则在中间纪录的左半区继续查找;若给定值大于中间纪录的关键字,则在中间纪录的右半边。不断重复上述过程,直到查找成功,或所有查找区域无记录,查找失败为止。
(2)使用条件:线性表中的纪录是关键码有序的(通常是从小到大有序),线性表必须采用顺序存储,即有序表顺序存储。
(3)算法实现
/*折半查找
* a为线性表数组,n为数据元素总个数,key为要查找的关键值*/
int Binary_Search(int *a,int n,int key)
{
int low,high,mid;
low=1; //定义最低下标为纪录首位
high=n;
while(low<=high)
{
mid=(low+high)/2; //折半(取整)
if(key<a[mid]) //若查找值比中值小
high=mid-1; //最高下标调整到中位小一伟
else if(key>a[mid]) //若查找值比中值大
low=mid+1; //最低下标调整到中位下标大一位
else
return mid; //若相等则说明Mid即为查找到的位置,返回该位置地址
}
return 0;
}
(4)举例
假设有一有序表a={0,1,16,24,35,47,59,62,73,88,99},n=10,key=62。即除0下标外共10个数字,对它进行查找是否存在62这个数。
a.查找步骤:
第一步:.a[mid]=a[5]=47<key,则low=mid+1=6,此时,mid=(6+10)=8
第二步:a[mid]=a[8]=73>key,则high=mid-1=7,此时,mid=(6+7)/2=6
第三步:a[mid]=a[6]=59<key,则low=mid+1=7,此时,mid=(low+high)=(7+7)/2=7
第四步:a[mid]=a[7]=key,查找成功。
b.时间复杂度分析
下面我们将这个数组的查找过程绘制成一棵二叉树如下:
由二叉树的性质4:"具有n个结点的完全二叉树的深度为[log2^n]+1",可知在最坏情况下查找到关键字或查找失败的次数为[log2^n]+1,最好情况为1次。相比于顺序查找的时间复杂度O(n),折半算法的时间复杂度为O(logn),显然效率高很多。
2.插值查找算法
在有序表查找中,虽然折半查找比顺序查找的查询效率提高了很多,但有些时候折半还是存在比较大的局限性。比如要在取值范围0~100000之间100个元素从小到大均匀分布的数据中查找5,我们自然会考虑从数组下标较小的开始查找,而不是从中间开始。
(1)插值查找法
插值查找是在折半查找算法的改进,为另一种有序表查找算法。插值查找(Interpolation Search)是根据要查找的关键字key与查找表中最大最小纪录的关键字比较后的查找方法,其核心就在于插值的计算公式(key-a[low])/(a[high]-a[low]),即mid=low+(key-a[low])/(a[high]-a[low])。
(2)适用条件:表长较大且关键字分布比较均匀的有序表。
(3)时间复杂度:O(logn)
(4)举例:
如上例中a={0,1,16,24,35,47,59,62,73,88,99},我们要查询关键字16。如果使用折半查找(mid=(low+high)/2),需要查找4次;如果使用插值查找(mid=low+(key-a[low])/(a[high]-a[low])~=2),即只需两次。
3.斐波那契查找
(1)斐波那契数列
斐波那契数列描述的是兔子的繁殖问题,这个数列有个十分明显的特点:前面相邻两项之和,构成了后一项。
其数学模型为:
| 0,当n=0时,其中n为月个数
F(n)=| 1,当n=1时
|F(n-1)+F(n-2),当n>1。其中n为经历的月个数,F(n)为第n个月时兔子的数量。
(2)算法实现
int Fibonacci_Search(int *a,int n,int key)
{
int low,high,mid,i,k;
low=1; //定义最低下标为纪录首位
high=n; //定义最高下标为纪录未位
k=0;
while(n>F[k]-1)
k++;
for(i=n;i<F[k]-1;i++) //将不满的数值补全
a[i]=a[n];
while(low<=high)
{
mid=low+F[k-1]-1;
if(key<a[mid])
{
high=mid-1;
k=k-1;
}
else if(key>a[mid]) //若查找纪录大于当前分隔纪录
{
low=mid+1; //最低下标调整到分隔下标mid+1处
k=k-2; //斐波那契数列下标减两位
}
else
{
if(mid<=n)
return mid; //若相等则说明mid即为查找的位置
else
return n; //若mid>n说明是补全数值,返回n
}
}
return 0;
}
二、线性索引查找
数据结构的最终目的就是提高数据的处理速度,索引是为了加快查找速度而设计的一种数据结构。索引就是把一个关键字与它对应的纪录相关联的过程,一个索引由若干个索引项构成,每个索引项至少包含关键字和其对应的纪录在存储器中的位置等信息。索引技术是组织大型数据库以及磁盘文件的一种重要技术。索引按照结构可以分为线性索引、树形索引和多级索引。所谓线性索引就是将索引项集合组织为线性结构,也成索引表。
1.稠密索引
稠密索引就是指在线性索引中,将数据集中的每个纪录对应一个索引项。对于稠密索引这个线索表而言,索引项一定是按照关键码有序的排列。
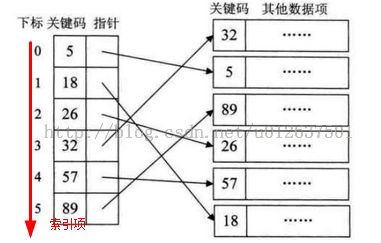
注意:索引表有序,即当我们要查找关键字时,可以用到折半、插值、斐波那契等有序查找算法,大大提高了效率。如下图,假如要查找的关键字是18的纪录,从右侧的数据表中查找,则只能顺序查找(需要6次);从左侧索引表中查找,则只需两次折半查找就可以得到18对应的指针。可见,线性索引查找目的就是将数据从无序变为有序,进而使用有序查找算法提供效率。
2.分块索引
稠密索引因为索引项与数据集的纪录个数相同,所以空间代价很大。为了减少索引项的个数,我们可以数据集进行分块,使其分块有序,然后再对每一块建立一个索引项,从而减少索引项的个数。
(1)分块有序原则
分块有序,即把数据集的纪录分成可若干块,并且这些快需要满足两个条件:
★块内无序,即每一块内的纪录不要求有序;
★块间有序,如第二块所有纪录的关键字均要大于第一块中所有纪录的关键字......;
(2)分块索引:对于分块有序的数据集,将每块对应一个索引项,这种索引方法叫做分块索引。其中,分块索引的索引项结构分三个数据项:
★最大关键码:用于存储对应块中的最大关键字,目的是使得在它之后的下一块的最小关键字也能比这一块最大的关键字要大;
★块长:存储了块中的纪录个数,以便于循环时使用;
★块首指针:用于指向块首数据元素的指针,便于开始对这一块中纪录进行遍历。
(3)分块索引表的查找过程
第一步:在分块索引表中查找要查的关键字所在的块;
第二步:根据块首指针找到相应的块,并在块中顺序查找关键码(块中纪录一般为无序)。
(4)分块索引的平均查找长度
设n个纪录的数据集被平均分成m块,每个块中有t条纪录,显然n=m*t,或者说m=n/t。
根据最好域最差的等概率原则:
Lb为查找索引表的平均查找长度=(m+1)/2;
Lw为查找某个纪录的平均查找长度=(t+1)/2;
可知,一次分块索引查找的平均查找长度为:ASLw=Lb+Lw=(m+1)/2+ (t+1)/2=(m+t)/2+1=(n/t+t)/2+1.即平均长度不仅仅取决于数据集的总记录数n,还和每一块的纪录个数t相关。
又n=m*t,ASLw=[(n/t+t)/2+1]>=[(n+t^2)/t]/2+1=[(m*t+t*t)/t]/2+1,假入m=t->t=√n,即分的块数m与块中的记录数t相
同,ASLw=√n +1时,为最好情况。O(n)<O(√n )<O(logn).
3.倒排索引
倒排索引源于实际应用中需要根据属性(或字段、次关键码)的值来查找纪录。