POJ 2299 Ultra-QuickSort 【归并排序 || 树状数组求逆序对数】
原题链接：http://poj.org/problem?id=2299
Ultra-QuickSort
| Time Limit: 7000MS | Memory Limit: 65536K | |
| Total Submissions: 31043 | Accepted: 11066 |
Description
In this problem, you have to analyze a particular sorting algorithm. The algorithm processes a sequence of n distinct integers by swapping two adjacent sequence elements until the sequence is sorted in ascending order. For the input sequence
9 1 0 5 4 ,
Ultra-QuickSort produces the output
0 1 4 5 9 .
Your task is to determine how many swap operations Ultra-QuickSort needs to perform in order to sort a given input sequence.
Input
The input contains several test cases. Every test case begins with a line that contains a single integer n < 500,000 -- the length of the input sequence. Each of the the following n lines contains a single integer 0 ≤ a[i] ≤ 999,999,999, the i-th input sequence element. Input is terminated by a sequence of length n = 0. This sequence must not be processed.
Output
For every input sequence, your program prints a single line containing an integer number op, the minimum number of swap operations necessary to sort the given input sequence.
Sample Input
5 9 1 0 5 4 3 1 2 3 0
Sample Output
6 0
Source
Waterloo local 2005.02.05
题意：求逆序数。
算法：归并排序，好像还有个树状数组的也可以解决，实在没弄明白，明天再想吧。。。
思路：归并合并时，一旦遇到前面一半的元素i大于后面一半中的元素j，那么就说明从素 i 开始一直到前面一半结束，每一个数都
和j组成逆序对，需交换。
注意：最坏的情况下 ans = 500000*500000/2要用long long型，开始没有注意WA了好久。
PS：应该算是很简单的一道题目了，KB神给我讲了一遍，还是看了好久才AC
明天继续树状数组版本。。。
5个月了, 重新学树状数组，终于明白了树状数组的解法Orz ————free斩 2013/8/11
//Accepted 3692 KB 391 ms C++ 750 B 2013-03-08 21:37:57
#include<cstdio>
#include<cstring>
const int maxn = 500000 + 10;
int a[maxn];
int t[maxn];
int n;
__int64 ans;
void merge_sort(int *a, int x, int y, int *t)
{
if(y-x > 1)
{
int m = x + (y-x)/2;
int p = x, q = m, i = x;
merge_sort(a, x, m, t);
merge_sort(a, m, y, t);
while(p < m && q < y) //合并
{
if(a[p] <= a[q]) t[i++] = a[p++];
else
{
t[i++] = a[q++];//a[p]>a[q]
ans += m-p;
}
}
while(p < m) t[i++] = a[p++];
while(q < y) t[i++] = a[q++];
for(i = x; i < y; i++) a[i] = t[i];
}
}
int main()
{
while(scanf("%d", &n) != EOF)
{
ans = 0;
if(n == 0) break;
for(int i = 0; i < n; i++)
scanf("%d", &a[i]);
merge_sort(a, 0, n, t);
printf("%I64d\n", ans);
}
return 0;
}
树状数组思路：树状数组+离散化
以前一直无法理解什么是离散化。也就一直无法用树状数组解决这题了。后来写了篇关于离散化的博客,这里就不再写那么详细了
hdu 2227 Find the nondecreasing subsequences【离散化+树状数组+DP思路】
关于这题的离散化：
因为 n < 500,000 ; 0 ≤ a[i] ≤ 999,999,999
主要也是把原来的区间【1, 999,999,999】映射到区间 【1, n】
这题的关键是求逆序数对的个数。什么是逆序数对？
a, b 如果 a 排在 b 前面而且 a > b 那么 a 和 b 就是一个逆序数对
下面看下题目的样例：
5
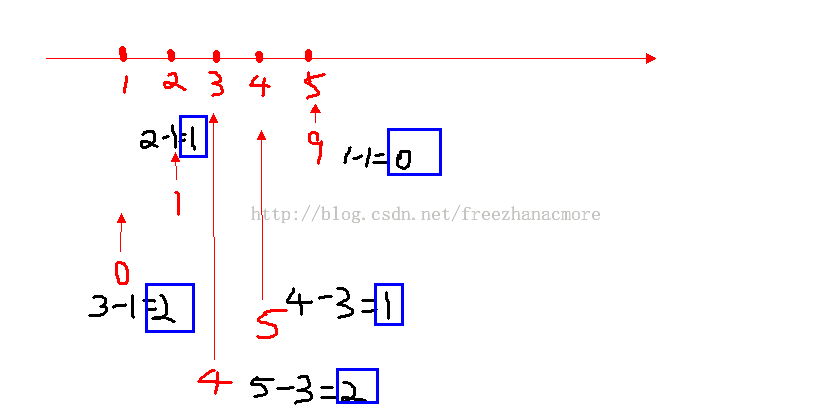
9 1 0 5 4
9前面比它大的个数 ： 0
1前面。。。。。。 ： 1
0.。。。。。。。 ： 2
5 ： 1
4 ： 2
总的 ans = 0+1+2+1+2 = 6
PS: 自己也可以按照这样的思路模拟交换排序, 肯定是排 6 次了, 这里不再详细说明。
如何应用与树状数组和离散化：
这里就不介绍说明是树状数组了。。。。
定义一个结构体存输入的数值和对应的编号
然后对编号进行离散化【也就是排序后对编号进行简单的处理】
先对元素值从小到大排序
b[i] //的下标 i 存的是第 i 大的初始的下标, 它的值表示当前元素第 b[i] 大
【这样就离散化了。。。把问题映射到了 1 到 N 这个区间】
然后再按照初始元素的输入的顺序依次将元素插入树状数组中。
遍历一个元素, 就在它的 b[i] 处 +1 表示此处添加了一个元素,
然后再计算他前面有多少个数比他大 sum(i) - sum(b[i])
以第一组数据为例：
初始元素： 9 1 0 5 4
逆序数对： 0 1 2 1 2
排序后： 0 1 4 5 9
对应初始编号： 3 2 5 4 1
那么先把 9 插入位置 5 , 前面有 0 个数比她大
把 1 插入位置 2 ， 前面有 1 个数比它大
把 0 插入位置 1 , 前面有 2 个数比它大
把 5 插入位置 3 ， 前面有 1 个数比它大
把 4 插入位置 4 , 前面有 2 个数比它大
【此处的前面对应于先插入的数。。。】
每次插入容易得到目前的总数就是 i
然后小于等于自己本身的数也容易计算 sum（b[i]）【插入的位置前面的数的个数。。。】
code：
#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
const int maxn = 500000+10;
__int64 c[maxn];
int b[maxn];
struct Node{
int val; //元素值
int index; // 编号
}a[maxn];
int n;
bool cmp(Node a, Node b) //从小到大排序
{
return a.val < b.val;
}
int lowbit(int x)
{
return x&(-x);
}
void add(int i, int val)
{
while(i <= n)
{
c[i] += val;
i += lowbit(i);
}
}
__int64 sum(int i)
{
__int64 ret = 0;
while(i > 0) //下标从 1 开始
{
ret += c[i];
i -= lowbit(i);
}
return ret;
}
int main()
{
while(scanf("%d", &n) != EOF)
{
if(n == 0) break;
memset(a, 0, sizeof(a));
memset(b, 0, sizeof(b));
memset(c, 0, sizeof(c));
for(int i = 1; i <= n; i++)
{
scanf("%d", &a[i].val);
a[i].index = i;
}
sort(a+1, a+n+1, cmp); // 从小到大排序
for(int i = 1; i <= n; i++) //离散化
{
b[a[i].index] = i; // b[i] 存原来编号为 i 的数现在第 b[i] 大
}
__int64 ans = 0;
for(int i = 1; i <= n; i++)
{
add(b[i], 1); // 按照初始输入顺序依次在树状数组中插入元素
ans += sum(n)-sum(b[i]); // 统计每个数前面比自己大的数的个数【目前总的个数减去小于等于当前数值的数目】
//ans += i - sum(b[i]); 也一样
}
printf("%I64d\n", ans);
}
return 0;
}
利用树状数组离散化求逆序数，看了很久，还是无法完全理解，贴个KB神的用树状数组求解的代码吧。。。
http://www.cnblogs.com/kuangbin/archive/2012/08/09/2630042.html
/*
POJ 2299 Ultra-QuickSort
求逆序数
离散化+树状数组
首先从小到大进行编号，从而实现离散化
然后利用树状数组来统计每个数前面比自己大的数的个数
*/
#include<stdio.h>
#include<string.h>
#include<algorithm>
#include<iostream>
using namespace std;
const int MAXN=500010;
int c[MAXN];
int b[MAXN];
int n;
struct Node
{
int index;//序号
int v;
}node[MAXN];
bool cmp(Node a,Node b)
{
return a.v<b.v;
}
int lowbit(int x)
{
return x&(-x);
}
void add(int i,int val)
{
while(i<=n)
{
c[i]+=val;
i+=lowbit(i);
}
}
int sum(int i)
{
int s=0;
while(i>0)
{
s+=c[i];
i-=lowbit(i);
}
return s;
}
int main()
{
// freopen("in.txt","r",stdin);
//freopen("out.txt","w",stdout);
while(scanf("%d",&n),n)
{
for(int i=1;i<=n;i++)
{
scanf("%d",&node[i].v);
node[i].index=i;
}
memset(b,0,sizeof(b));
memset(c,0,sizeof(c));
//离散化
sort(node+1,node+n+1,cmp);
//将最小的编号为1
b[node[1].index]=1;
for(int i=2;i<=n;i++)
{
if(node[i].v!=node[i-1].v) b[node[i].index]=i;
else b[node[i].index]=b[node[i-1].index];
}
long long ans=0;
//这里用的很好
//一开始c数组都是0，然后逐渐在b[i]处加上1；
for(int i=1;i<=n;i++)
{
add(b[i],1);
ans+=i-sum(b[i]); //统计每个数前面比自己大的数的个数
}
printf("%I64d\n",ans);
}
return 0;
}