Opencv学习二:角点检测
内容一:角点的基础知识
详见附件。(包括角点检测的定义、分类以及常用的两种角点检测算法接好(harris和susan),并讨论他们的优缺点)
内容二:harris角点检测的理论基础以及算法描述(详见附件中的ppt)
角点响应
R=det(M)-k*(trace(M)^2) (附录资料给出k=0.04~0.06,opencv指出是0.05-0.5,浮动较大)
det(M)=λ1*λ2 trace(M)=λ1+λ2
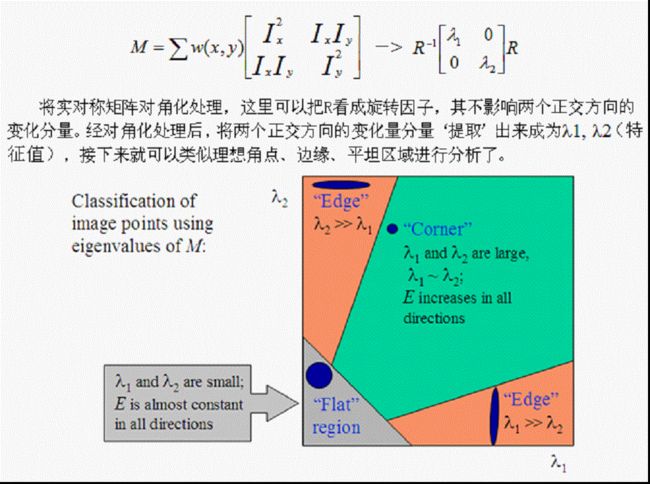
R取决于M的特征值,对于角点|R|很大,平坦的区域|R|很小,边缘的R为负值。
算法描述:
内容三:harris角点检测算法的opencv实现(该部分转自http://blog.csdn.net/crzy_sparrow/article/details/7391511)
#ifndef HARRIS_H
#define HARRIS_H
#include "opencv2/opencv.hpp"
class harris
{
private:
cv::Mat cornerStrength; //opencv harris函数检测结果,也就是每个像素的角点响应函数值
cv::Mat cornerTh; //cornerStrength阈值化的结果
cv::Mat localMax; //局部最大值结果
int neighbourhood; //邻域窗口大小
int aperture;//sobel边缘检测窗口大小(sobel获取各像素点x,y方向的灰度导数)
double k;
double maxStrength;//角点响应函数最大值
double threshold;//阈值除去响应小的值
int nonMaxSize;//这里采用默认的3,就是最大值抑制的邻域窗口大小
cv::Mat kernel;//最大值抑制的核,这里也就是膨胀用到的核
public:
harris():neighbourhood(3),aperture(3),k(0.01),maxStrength(0.0),threshold(0.01),nonMaxSize(3){
};
void setLocalMaxWindowsize(int nonMaxSize){
this->nonMaxSize = nonMaxSize;
};
//计算角点响应函数以及非最大值抑制
void detect(const cv::Mat &image){
//opencv自带的角点响应函数计算函数
cv::cornerHarris (image,cornerStrength,neighbourhood,aperture,k);
double minStrength;
//计算最大最小响应值
cv::minMaxLoc (cornerStrength,&minStrength,&maxStrength);
cv::Mat dilated;
//默认3*3核膨胀,膨胀之后,除了局部最大值点和原来相同,其它非局部最大值点被
//3*3邻域内的最大值点取代
cv::dilate (cornerStrength,dilated,cv::Mat());
//与原图相比,只剩下和原图值相同的点,这些点都是局部最大值点,保存到localMax
cv::compare(cornerStrength,dilated,localMax,cv::CMP_EQ);
}
//获取角点图
cv::Mat getCornerMap(double qualityLevel) {
cv::Mat cornerMap;
// 根据角点响应最大值计算阈值
threshold= qualityLevel*maxStrength;
cv::threshold(cornerStrength,cornerTh,
threshold,255,cv::THRESH_BINARY);
// 转为8-bit图
cornerTh.convertTo(cornerMap,CV_8U);
// 和局部最大值图与,剩下角点局部最大值图,即:完成非最大值抑制
cv::bitwise_and(cornerMap,localMax,cornerMap);
return cornerMap;
}
void getCorners(std::vector<cv::Point> &points,
double qualityLevel) {
//获取角点图
cv::Mat cornerMap= getCornerMap(qualityLevel);
// 获取角点
getCorners(points, cornerMap);
}
// 遍历全图,获得角点
void getCorners(std::vector<cv::Point> &points,
const cv::Mat& cornerMap) {
for( int y = 0; y < cornerMap.rows; y++ ) {
const uchar* rowPtr = cornerMap.ptr<uchar>(y);
for( int x = 0; x < cornerMap.cols; x++ ) {
// 非零点就是角点
if (rowPtr[x]) {
points.push_back(cv::Point(x,y));
}
}
}
}
//用圈圈标记角点
void drawOnImage(cv::Mat &image,
const std::vector<cv::Point> &points,
cv::Scalar color= cv::Scalar(255,255,255),
int radius=3, int thickness=2) {
std::vector<cv::Point>::const_iterator it=points.begin();
while (it!=points.end()) {
// 角点处画圈
cv::circle(image,*it,radius,color,thickness);
++it;
}
}
};
#endif // HARRIS_H
cv::Mat image, image1 = cv::imread ("test.jpg");
//灰度变换
cv::cvtColor (image1,image,CV_BGR2GRAY);
// 经典的harris角点方法
harris Harris;
// 计算角点
Harris.detect(image);
//获得角点
std::vector<cv::Point> pts;
Harris.getCorners(pts,0.01);
// 标记角点
Harris.drawOnImage(image,pts);
cv::namedWindow ("harris");
cv::imshow ("harris",image);
cv::waitKey (0);
return 0;
改进的Harris角点检测
从经典的Harris角点检测方法不难看出,该算法的稳定性和k有关,而k是个经验值,不好把握,浮动也有可能较大。鉴于此,改进的Harris方法()直接计算出两个特征值,通过比较两个特征值直接分类,这样就不用计算Harris响应函数了。
另一方面,我们不再用非极大值抑制了,而选取容忍距离:容忍距离内只有一个特征点。
该算法首先选取一个具有最大 最小特征值的点(即:max(min(e1,e2)),e1,e2是harris矩阵的特征值)作为角点,然后依次按照最大最小特征值顺序寻找余下的角点,当然和前一角点距离在容忍距离内的新角点呗忽略。
opencv测试该算法代码如下:
cv::Mat image, image1 = cv::imread ("test.jpg");
//灰度变换
cv::cvtColor (image1,image,CV_BGR2GRAY);
// 改进的harris角点检测方法
std::vector<cv::Point> corners;
cv::goodFeaturesToTrack(image,corners,
200,
//角点最大数目
0.01,
// 质量等级,这里是0.01*max(min(e1,e2)),e1,e2是harris矩阵的特征值
10);
// 两个角点之间的距离容忍度
harris().drawOnImage(image,corners);//标记角点
内容四:harris角点检测算法的C语言实现(该部分来自百度文库,但是自己要仔细详读,其实就是按照算法描述的步骤进行的,在角点计算完成后,该代码阈值是固定的,笔者所用阈值是根据提取特征点的个数动态设定的)
void Harry(BYTE*BBuf,BYTE*GBuf,BYTE*RBuf)
{
//gausswidth:二维高斯窗口宽度
//sigma:高斯函数的方差
//size:非极大值抑制的邻域宽度
//thresh:最终确定角点所需的阈值
int i,j,m,n,size,thresh,gausswidth;
double sigma;
//输入四个参数
//CInput2 input;
//input.m_gausswidth =5;
//input.m_sigma =0.8;
//input.m_size =5;
//input.m_thresh =5000;
//input.DoModal ();
gausswidth=5;//input.m_gausswidth ;
sigma=0.8;//input.m_sigma ;
size=5;//input.m_size ;
thresh=5000;//input.m_thresh ;
unsigned char *lpSrc;//一个指向源、目的像素的移动指针
//LPSTR lpDIB = (LPSTR) ::GlobalLock((HGLOBAL)m_hDIB);
int cxDIB = 320;//(int) ::DIBWidth(lpDIB); // 图像宽度
int cyDIB = 240;//(int) ::DIBHeight(lpDIB); // 图像高度
//LPSTR lpDIBBits=::FindDIBBits (lpDIB);
long lLineBytes = 320;//WIDTHBYTES(cxDIB * 8); // 计算灰度图像每行的字节数
//创建I、Ix、Ix2、Iy、Iy2、Ixy、cim、mx、corner数组
double *I=new double[cxDIB*cyDIB];
double *Ix=new double[cxDIB*cyDIB];
double *Ix2=new double[cxDIB*cyDIB];
double *Iy=new double[cxDIB*cyDIB];
double *Iy2=new double[cxDIB*cyDIB];
double *Ixy=new double[cxDIB*cyDIB];
double *cim=new double[cxDIB*cyDIB];
double *mx=new double[cxDIB*cyDIB];
bool*corner=new bool[cxDIB*cyDIB];
memset(corner, 0, cxDIB*cyDIB*sizeof(bool));
//定义宏以方便访问元素
#define I(ROW,COL) I[cxDIB*(ROW)+(COL)]
#define Ix(ROW,COL) Ix[cxDIB*(ROW)+(COL)]
#define Ix2(ROW,COL) Ix2[cxDIB*(ROW)+(COL)]
#define Iy(ROW,COL) Iy[cxDIB*(ROW)+(COL)]
#define Iy2(ROW,COL) Iy2[cxDIB*(ROW)+(COL)]
#define Ixy(ROW,COL) Ixy[cxDIB*(ROW)+(COL)]
#define cim(ROW,COL) cim[cxDIB*(ROW)+(COL)]
#define mx(ROW,COL) mx[cxDIB*(ROW)+(COL)]
#define corner(ROW,COL) corner[cxDIB*(ROW)+(COL)]
//将图像灰度值复制到I中,这步很重要!想想为什么?
for(i = 0; i < cyDIB; i++)
{
for(j = 0; j < cxDIB; j++)
{
lpSrc = (unsigned char*)BBuf + lLineBytes * (cyDIB - 1 - i) + j;
//将256级灰度图像转化为double型
I(i,j)=double(*lpSrc);
}
}
//--------------------------------------------------------------------------
// 第一步:利用差分算子对图像进行滤波http://www.cnifx.cn/
//--------------------------------------------------------------------------
//定义水平方向差分算子并求Ix
double dx[9]={-1,0,1,-1,0,1,-1,0,1};
Ix=mbys(I,cxDIB,cyDIB,&dx[0],3,3);
//定义垂直方向差分算子并求Iy
double dy[9]={-1,-1,-1,0,0,0,1,1,1};
Iy=mbys(I,cxDIB,cyDIB,dy,3,3);
//将中间结果Ix写入到文本文件以便后续分析
FILE *fp;
fp=fopen("Ix.txt","w+");
for(i = 0; i < cyDIB; i++)
{
for(j = 0; j < cxDIB; j++)
fprintf(fp,"%f ",Ix(i,j));
fprintf(fp,"\n");
}
fp=fopen("Iy.txt","w+");
for(i = 0; i < cyDIB; i++)
{
for(j = 0; j < cxDIB; j++)
fprintf(fp,"%f ",Iy(i,j));
fprintf(fp,"\n");
}
//计算Ix2、Iy2、Ixy
for(i = 0; i < cyDIB; i++)
{
for(j = 0; j < cxDIB; j++)
{
Ix2(i,j)=Ix(i,j)*Ix(i,j);
Iy2(i,j)=Iy(i,j)*Iy(i,j);
Ixy(i,j)=Ix(i,j)*Iy(i,j);
}
}
//--------------------------------------------------------------------------
// 第二步:对Ix2/Iy2/Ixy进行高斯平滑,以去除噪声http://www.cnifx.cn/
//--------------------------------------------------------------------------
//本例中使用5×5的高斯模板
//计算模板参数
double *g=new double[gausswidth*gausswidth];
for(i=0;i<gausswidth;i++)
for(j=0;j<gausswidth;j++)
g[i*gausswidth+j]=exp(-((i-int(gausswidth/2))*(i-int(gausswidth/2))+(j-int(gausswidth/2))*(j-int(gausswidth/2)))/(2*sigma));
//归一化:使模板参数之和为1(其实此步可以省略)
double total=0;
for(i=0;i<gausswidth*gausswidth;i++)
total+=g[i];
for(i=0;i<gausswidth;i++)
for(j=0;j<gausswidth;j++)
g[i*gausswidth+j]/=total;
fp=fopen("g.txt","w+");
for(i = 0; i < gausswidth; i++)
{
for(j = 0; j < gausswidth; j++)
fprintf(fp,"%f ",g[i*gausswidth+j]);
fprintf(fp,"\n");
}
//进行高斯平滑
Ix2=mbys(Ix2,cxDIB,cyDIB,g,gausswidth,gausswidth);
Iy2=mbys(Iy2,cxDIB,cyDIB,g,gausswidth,gausswidth);
Ixy=mbys(Ixy,cxDIB,cyDIB,g,gausswidth,gausswidth);
//--------------------------------------------------------------------------
// 第三步:计算角点量http://www.cnifx.cn/
//--------------------------------------------------------------------------
//计算cim:即cornerness of image,我们把它称做'角点量'
for(i = 0; i < cyDIB; i++)
{
for(j = 0; j < cxDIB; j++)
{
//注意:要在分母中加入一个极小量以防止除数为零溢出
cim(i,j) = (Ix2(i,j)*Iy2(i,j) - Ixy(i,j)*Ixy(i,j))/(Ix2(i,j) + Iy2(i,j) + 0.000001);
}
}
fp=fopen("cim.txt","w+");
for(i = 0; i < cyDIB; i++)
{
for(j = 0; j < cxDIB; j++)
fprintf(fp,"%f ",cim(i,j));
fprintf(fp,"\n");
}
//--------------------------------------------------------------------------
// 第四步:进行局部非极大值抑制以获得最终角点http://www.cnifx.cn/
//--------------------------------------------------------------------------
//注意进行局部极大值抑制的思路
//const double size=7;
double max;
//对每个点在邻域内做极大值滤波:即将该点的值设为邻域中最大的那个值(跟中值滤波有点类似)
for(i = 0; i < cyDIB; i++)
{
for(j = 0; j < cxDIB; j++)
{
max=-1000000;
if(i>int(size/2) && i<cyDIB-int(size/2) && j>int(size/2) && j<cxDIB-int(size/2))
for(m=0;m<size;m++)
{
for(n=0;n<size;n++)
{
if(cim(i+m-int(size/2),j+n-int(size/2))>max)
max=cim(i+m-int(size/2),j+n-int(size/2));
}
}
if(max>0)
mx(i,j)=max;
else
mx(i,j)=0;
}
}
fp=fopen("mx.txt","w+");
for(i = 0; i < cyDIB; i++)
{
for(j = 0; j < cxDIB; j++)
fprintf(fp,"%f ",mx(i,j));
fprintf(fp,"\n");
}
//最终确定角点
//const double thresh=4500;
for(i = 0; i < cyDIB; i++)
{
for(j = 0; j < cxDIB; j++)
{
if(cim(i,j)==mx(i,j)) //首先取得局部极大值
if(mx(i,j)>thresh) //然后大于这个阈值
corner(i,j)=1; //满足上两个条件,才是角点!
}
}
fp=fopen("corner.txt","w+");
for(i = 0; i < cyDIB; i++)
{
for(j = 0; j < cxDIB; j++)
fprintf(fp,"%d ",corner(i,j));
fprintf(fp,"\n");
}
//::GlobalUnlock((HGLOBAL) m_hDIB);
// UpdateAllViews(NULL, 0, NULL);
}
double * mbys(double * im,int imW,int imH,double *tp,int tpW,int tpH)
{
double * out=new double[imW*imH];
memset(out, 0, imW*imH*sizeof(double));
int i,j,m,n;
#define im(ROW,COL) im[imW*(ROW)+(COL)]
#define tp(ROW,COL) tp[tpW*(ROW)+(COL)]
#define out(ROW,COL) out[imW*(ROW)+(COL)]
double a;
for(i=0;i<imH;i++)
for(j=0;j<imW;j++)
{
a=0;
//去掉靠近边界的行
if(i>int(tpH/2) && i<imH-int(tpH/2) && j>int(tpW/2) && j<imW-int(tpW/2))
for(m=0;m<tpH;m++)
for(n=0;n<tpW;n++)
{
a+=im(i+m-int(tpH/2),j+n-int(tpW/2))*tp(m,n);
}
out(i,j)=a;
}
return out;
}
内容五:susan角点检测算法
该算法的角点定义为:若某像素点圆形邻域圆周上有3/4的点和该像素点不同(编程时不超过某阈值th),则认为该点就是候选角点。opencv更极端,选用半径为3的圆周上(上下左右)四个点,若超过三个点和该像素点不同,则该点为候选角点。(该部分同样转载自http://blog.csdn.net/crzy_sparrow/article/details/7391511)
和Harris算法类似,该算法需要非极大值抑制。
cv::Mat image, image1 = cv::imread ("test.jpg");
cv::cvtColor (image1,image,CV_BGR2GRAY);
//快速角点检测
std::vector<cv::KeyPoint> keypoints;
cv::FastFeatureDetector fast(40,true);
fast .detect (image,keypoints);
cv::drawKeypoints (image,keypoints,image,cv::Scalar::all(255),cv::DrawMatchesFlags::DRAW_OVER_OUTIMG);
至于其C语言的实现,主要模板的和阈值的选取,在http://ar.newsmth.net/thread-56d09414bec7d.html这篇帖子中有一个实现的例子。