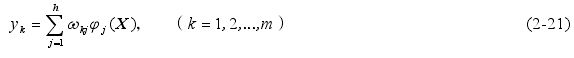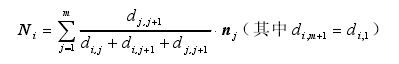三角网格模型及基于RBF隐曲面方程求解的曲面重建
资料来源:径向基函数和神经网络技术在逆向工程中的应用研究(博士论文:王宏涛)
RBF神经网络模型
RBF神经网络起源于数值分析中多变量插值的RBF方法,1988年Broomhead等人首先将该算法应用于神经网络的设计,从而构成了RBF神经网络。
RBF神经网络是一种由输入层、隐层和输出层组成的三层前馈型网络,其结构简图如图2.3所示[120]。输入层节点只传递输入信号到隐层,从输入层到隐层的变换是非线性的,隐层节点由一定的作用函数构成,从隐层到输出层的变换是线性的。输入层到隐层之间的权固定为1,只有隐层到输出层之间的权可调。
隐层的变换函数是一种局部分布的、对中心点径向对称衰减的非负线性函数,其常用的函数形式是高斯函数
图1示意出了三角网格模型的各单纯形的邻域,对图中用方形所示的任意顶点v,其一重邻点为图中所示的黑圆点,其二重邻点(即顶点v的一
重邻点的一重邻点)为图中所示的黑三角点,其邻边为图中所示的粗黑线,其邻三角片为图中所示的阴影中的各三角片。
如图2所示,对三角网格曲面M中的一个顶点vi,设其有m个一重邻点vj(j=1,2,…m)∈nbhd{i},则其有m个邻三角片f
j(j=1,2,…m)。设nj是fj的单位法矢,di,j是eij的长度,采用柯映林[108]从力学角度给出的单位法矢加权叠加的方法,可计算顶点vi的法矢Ni:
在不少文献[123~125]中,用相邻三角片法矢与三角片面积的加权来获得顶点的法矢,设Nfi是三角片fj的法矢,Aj是三角片fj的面积,顶点vi的法矢Ni为:
[108] 柯映林.散乱数据几何造型技术及其应用研究[博士学位论文].南京,南京航空航天大学,1992.
[123] Taubin G.Estimating the tensor of curvature of a surface from a polyhedral approximation.In:Proc.5th Intl.Conf.on Computer Vision(ICCV’95),1995:902~907.
[124] Biermann H,Levin A,Zorin D.Piecewise smooth subdivision surfaces with normal control.In:K.Akeley ed.,Proceedings of SIGGRAPH’2000.Boston,MA:Addision Wesley Professional,2000:113~120.
[125] Page D L,Koschan A,Sun Y,et al.Robust crease detection and curvature estimation of piecewise smooth surfaces from triangle mesh approximations using normal voting.In:C.E. Brodley,A.P.Danyluk ed.,Proceedings of the International Conference on Computer Vision and Pattern Recognition 2001.San Francisco,CA:Morgan Kaufmann,2001:162~167.
[126]周儒荣,张丽艳,苏旭,等.海量散乱点的曲面重建算法研究.软件学报,2001, 12(2):249~255.
[129]刘利刚,王国瑾.基于球面三角网格逼近的等距曲面逼近算法.工程图学学报, 2000(3):70~74.