Lucene之MinShouldMatchScorer算法源码分析

   在lucene中检索出来的文档用倒排列表来表示，每个query Term对应一个倒排列表。每个列表的长度则

表示有多少篇文档含有该Term。那么在Lucene中大部分的查询都是Boolean查询（AND，OR，NOT），对于AND

来说，直接对倒排列表求交集就可以了，由于倒排列表采用跳跃表结构，所以求交比较快，具体过程参见大

牛觉先的blog（http://www.cnblogs.com/forfuture1978/archive/2010/04/04/1704258.html），但是对于

OR操作来说则是求并集，原先的DisjunctionSumScorer中有成员变量List<Scorer> subScorers，是一个Scorer

的链表，每一项代表一个倒排表，DisjunctionSumScorer就是对这些倒排表取并集，然后将并集中的文档号在nextDoc()函数中依次返回。DisjunctionSumScorer有一个成员变量minimumNrMatchers，表示最少需满足的子

条件的个数，也即subScorer中，必须有至少minimumNrMatchers个Scorer都包含某个文档号，此文档号才能够

返回，具体流程如下（转自觉先blog：http://write.blog.csdn.net/postedit/12614525）

(1) 假设minimumNrMatchers = 4，倒排表最初如下：

(2) 在DisjunctionSumScorer的构造函数中，将倒排表放入一个优先级队列scorerDocQueue中(scorerDocQueue的实现是一个最小堆)，队列中的Scorer按照第一篇文档的大小排序。

private void initScorerDocQueue() throws IOException {   scorerDocQueue = new ScorerDocQueue(nrScorers);   for (Scorer se : subScorers) {     if (se.nextDoc() != NO_MORE_DOCS) { //此处的nextDoc使得每个Scorer得到第一篇文档号。       scorerDocQueue.insert(se);     }   } }

(3) 当BooleanScorer2.score(Collector)中第一次调用nextDoc()的时候，advanceAfterCurrent被调用。

public int nextDoc() throws IOException {   if (scorerDocQueue.size() < minimumNrMatchers || !advanceAfterCurrent()) {     currentDoc = NO_MORE_DOCS;   }   return currentDoc; }

protected boolean advanceAfterCurrent() throws IOException {   do {     currentDoc = scorerDocQueue.topDoc(); //当前的文档号为最顶层     currentScore = scorerDocQueue.topScore(); //当前文档的打分     nrMatchers = 1; //当前文档满足的子条件的个数，也即包含当前文档号的Scorer的个数     do {       //所谓topNextAndAdjustElsePop是指，最顶层(top)的Scorer取下一篇文档(Next)，如果能够取到，则最小堆的堆顶可能不再是最小值了，需要调整(Adjust，其实是downHeap())，如果不能够取到，则最顶层的Scorer已经为空，则弹出队列(Pop)。       if (!scorerDocQueue.topNextAndAdjustElsePop()) {         if (scorerDocQueue.size() == 0) {           break; // nothing more to advance, check for last match.         }       }       //当最顶层的Scorer取到下一篇文档，并且调整完毕后，再取出此时最上层的Scorer的第一篇文档，如果不是currentDoc，说明currentDoc此文档号已经统计完毕nrMatchers，则退出内层循环。       if (scorerDocQueue.topDoc() != currentDoc) {         break; // All remaining subscorers are after currentDoc.       }       //否则nrMatchers加一，也即又多了一个Scorer也包含此文档号。       currentScore += scorerDocQueue.topScore();       nrMatchers++;     } while (true);     //如果统计出的nrMatchers大于最少需满足的子条件的个数，则此currentDoc就是满足条件的文档，则返回true，在收集文档的过程中，DisjunctionSumScorer.docID()会被调用，返回currentDoc。     if (nrMatchers >= minimumNrMatchers) {       return true;     } else if (scorerDocQueue.size() < minimumNrMatchers) {       return false;     }   } while (true); }

advanceAfterCurrent具体过程如下：

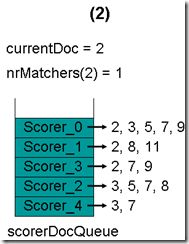
• 最初，currentDoc=2，文档2的nrMatchers=1

• 最顶层的Scorer 0取得下一篇文档，为文档3，重新调整最小堆后如下图。此时currentDoc等于最顶层Scorer 1的第一篇文档号，都为2，文档2的nrMatchers为2。

• 最顶层的Scorer 1取得下一篇文档，为文档8，重新调整最小堆后如下图。此时currentDoc等于最顶层Scorer 3的第一篇文档号，都为2，文档2的nrMatchers为3。

• 最顶层的Scorer 3取得下一篇文档，为文档7，重新调整最小堆后如下图。此时currentDoc还为2，不等于最顶层Scorer 2的第一篇文档3，于是退出内循环。此时检查，发现文档2的nrMatchers为3，小于minimumNrMatchers，不满足条件。于是currentDoc设为最顶层Scorer 2的第一篇文档3，nrMatchers设为1，重新进入下一轮循环。

• 最顶层的Scorer 2取得下一篇文档，为文档5，重新调整最小堆后如下图。此时currentDoc等于最顶层Scorer 4的第一篇文档号，都为3，文档3的nrMatchers为2。

• 最顶层的Scorer 4取得下一篇文档，为文档7，重新调整最小堆后如下图。此时currentDoc等于最顶层Scorer 0的第一篇文档号，都为3，文档3的nrMatchers为3。

• 最顶层的Scorer 0取得下一篇文档，为文档5，重新调整最小堆后如下图。此时currentDoc还为3，不等于最顶层Scorer 0的第一篇文档5，于是退出内循环。此时检查，发现文档3的nrMatchers为3，小于minimumNrMatchers，不满足条件。于是currentDoc设为最顶层Scorer 0的第一篇文档5，nrMatchers设为1，重新进入下一轮循环。

• 最顶层的Scorer 0取得下一篇文档，为文档7，重新调整最小堆后如下图。此时currentDoc等于最顶层Scorer 2的第一篇文档号，都为5，文档5的nrMatchers为2。

 

• 最顶层的Scorer 2取得下一篇文档，为文档7，重新调整最小堆后如下图。此时currentDoc还为5，不等于最顶层Scorer 2的第一篇文档7，于是退出内循环。此时检查，发现文档5的nrMatchers为2，小于minimumNrMatchers，不满足条件。于是currentDoc设为最顶层Scorer 2的第一篇文档7，nrMatchers设为1，重新进入下一轮循环。

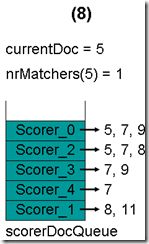
• 最顶层的Scorer 2取得下一篇文档，为文档8，重新调整最小堆后如下图。此时currentDoc等于最顶层Scorer 3的第一篇文档号，都为7，文档7的nrMatchers为2。

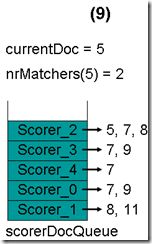
• 最顶层的Scorer 3取得下一篇文档，为文档9，重新调整最小堆后如下图。此时currentDoc等于最顶层Scorer 4的第一篇文档号，都为7，文档7的nrMatchers为3。

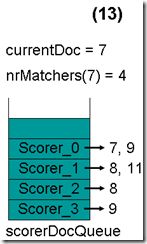
• 最顶层的Scorer 4取得下一篇文档，结果为空，Scorer 4所有的文档遍历完毕，弹出队列，重新调整最小堆后如下图。此时currentDoc等于最顶层Scorer 0的第一篇文档号，都为7，文档7的nrMatchers为4。

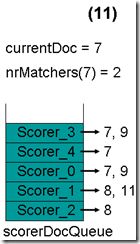
• 最顶层的Scorer 0取得下一篇文档，为文档9，重新调整最小堆后如下图。此时currentDoc还为7，不等于最顶层Scorer 1的第一篇文档8，于是退出内循环。此时检查，发现文档7的nrMatchers为4，大于等于minimumNrMatchers，满足条件，返回true，退出外循环。

(4) currentDoc设为7，在收集文档的过程中，DisjunctionSumScorer.docID()会被调用，返回currentDoc，也即当前的文档号为7。

(5) 当再次调用nextDoc()的时候，文档8, 9, 11都不满足要求，最后返回NO_MORE_DOCS，倒排表合并结束。

以上分析过程转自觉先blog

但是这样就需要一次pop出每个docid来进行判断。效率比较慢。

Stefan Pohl 认为现在的跳跃表已经使ConjunctionScorer（交集）很高效了，那么能不能在利用MinShouldMatch这个条件在DisjunctionSumScorer（并集）中最大化求交集呐？他的做法是先从subScorers list中取出MinShouldMatch-1个scorer存入一个数组mmstack中，剩下的存入heap，首先从heap中获取候选的docid，count heap中当前匹配的docid个数，然后再拿这个docid和数组mmstack中的每个scorer的倒排列表进行求交，计算MinShouldMatch是否满足要求。

具体实现参加以下关键源码（源文件在lucene发布的4.3.0版本中org.apache.lucene.search.MinShouldMatchSumScorer.java）：

class MinShouldMatchSumScorer extends Scorer {

  /** The overall number of non-finalized scorers */
  private int numScorers;
  /** The minimum number of scorers that should match */
  private final int mm;

  /** A static array of all subscorers sorted by decreasing cost */
  private final Scorer sortedSubScorers[];
  /** A monotonically increasing index into the array pointing to the next subscorer that is to be excluded */
  private int sortedSubScorersIdx = 0;

  private final Scorer subScorers[]; // the first numScorers-(mm-1) entries are valid
  private int nrInHeap; // 0..(numScorers-(mm-1)-1)

  /** mmStack is supposed to contain the most costly subScorers that still did
   *  not run out of docs, sorted by increasing sparsity of docs returned by that subScorer.
   *  For now, the cost of subscorers is assumed to be inversely correlated with sparsity.
   */
  private final Scorer mmStack[]; // of size mm-1: 0..mm-2, always full

  /** The document number of the current match. */
  private int doc = -1;
  /** The number of subscorers that provide the current match. */
  protected int nrMatchers = -1;
  private double score = Float.NaN;

  /**
   * Construct a <code>MinShouldMatchSumScorer</code>.
   * 
   * @param weight The weight to be used.
   * @param subScorers A collection of at least two subscorers.
   * @param minimumNrMatchers The positive minimum number of subscorers that should
   * match to match this query.
   * <br>When <code>minimumNrMatchers</code> is bigger than
   * the number of <code>subScorers</code>, no matches will be produced.
   * <br>When minimumNrMatchers equals the number of subScorers,
   * it is more efficient to use <code>ConjunctionScorer</code>.
   */
  public MinShouldMatchSumScorer(List<Scorer> subScorersList, int minimumNrMatchers) throws IOException {
    super(null);
    this.nrInHeap = this.numScorers = subScorersList.size();
    
    if (minimumNrMatchers <= 0) {
      throw new IllegalArgumentException("Minimum nr of matchers must be positive");
    }
    if (numScorers <= 1) {
      throw new IllegalArgumentException("There must be at least 2 subScorers");
    }

    this.mm = minimumNrMatchers;
    this.sortedSubScorers = subScorersList.toArray(new Scorer[this.numScorers]);
    // sorting by decreasing subscorer cost should be inversely correlated with
    // next docid (assuming costs are due to generating many postings)
/**
* 这个排序是其优化步骤之一，为什么要用cost（）排序？？？
*/
ArrayUtil.mergeSort(sortedSubScorers, new Comparator<Scorer>() {
      @Override
      public int compare(Scorer o1, Scorer o2) {
        //return Long.signum(o2.docID() - o1.docID());
        return Long.signum(o2.cost() - o1.cost());
      }
    });
    // take mm-1 most costly subscorers aside
    this.mmStack = new Scorer[mm-1];
    for (int i = 0; i < mm-1; i++) {
      mmStack[i] = sortedSubScorers[i];
    }
    nrInHeap -= mm-1;
    this.sortedSubScorersIdx = mm-1;
    // take remaining into heap, if any, and heapify
    this.subScorers = new Scorer[nrInHeap];
    for (int i = 0; i < nrInHeap; i++) {
      this.subScorers[i] = this.sortedSubScorers[mm-1+i];
    }
    
    minheapHeapify();
    assert minheapCheck();
  }
@Override
  public int nextDoc() throws IOException {
    assert doc != NO_MORE_DOCS;
    while (true) {
      // to remove current doc, call next() on all subScorers on current doc within heap
      while (subScorers[0].docID() == doc) {
        if (subScorers[0].nextDoc() != NO_MORE_DOCS) {
          minheapSiftDown(0);
        } else {
          minheapRemoveRoot();
          numScorers--;
          if (numScorers < mm) {
            return doc = NO_MORE_DOCS;
          }
        }
        //assert minheapCheck();
      }

      evaluateSmallestDocInHeap();

      if (nrMatchers >= mm) { // doc satisfies mm constraint
        break;
      }
    }
    return doc;
  }
  
  private void evaluateSmallestDocInHeap() throws IOException {
    // within heap, subScorer[0] now contains the next candidate doc
    doc = subScorers[0].docID();
    if (doc == NO_MORE_DOCS) {
      nrMatchers = Integer.MAX_VALUE; // stop looping
      return;
    }
    // 1. score and count number of matching subScorers within heap
    score = subScorers[0].score();
    nrMatchers = 1;
    countMatches(1);
    countMatches(2);
    // 2. score and count number of matching subScorers within stack,
    // short-circuit: stop when mm can't be reached for current doc, then perform on heap next()
    // TODO instead advance() might be possible, but complicates things
    for (int i = mm-2; i >= 0; i--) { // first advance sparsest subScorer
      if (mmStack[i].docID() >= doc || mmStack[i].advance(doc) != NO_MORE_DOCS) {
        if (mmStack[i].docID() == doc) { // either it was already on doc, or got there via advance()
          nrMatchers++;
          score += mmStack[i].score();
        } else { // scorer advanced to next after doc, check if enough scorers left for current doc
          if (nrMatchers + i < mm) { // too few subScorers left, abort advancing
            return; // continue looping TODO consider advance() here
          }
        }
      } else { // subScorer exhausted
        numScorers--;
        if (numScorers < mm) { // too few subScorers left
          doc = NO_MORE_DOCS;
          nrMatchers = Integer.MAX_VALUE; // stop looping
          return;
        }
        if (mm-2-i > 0) {
          // shift RHS of array left
          System.arraycopy(mmStack, i+1, mmStack, i, mm-2-i);
        }
        // find next most costly subScorer within heap TODO can this be done better?
        while (!minheapRemove(sortedSubScorers[sortedSubScorersIdx++])) {
          //assert minheapCheck();
        }
        // add the subScorer removed from heap to stack
        mmStack[mm-2] = sortedSubScorers[sortedSubScorersIdx-1];
        
        if (nrMatchers + i < mm) { // too few subScorers left, abort advancing
          return; // continue looping TODO consider advance() here
        }
      }
    }
  }

//省略一些不是算法关键的部分

}

1、首先对subScorers进行按cost()值降序排序，关于cost() 函数的意思，4.3.0API解释：

/**
   * Returns the estimated cost of this {@link DocIdSetIterator}.
   * <p>
   * This is generally an upper bound of the number of documents this iterator
   * might match, but may be a rough heuristic, hardcoded value, or otherwise
   * completely inaccurate.
   */
  public abstract long cost();

2、如何最大化进行求交集的数组呐？对 subScorers排序之后把倒排列表最长的mm-1个Scorer存入了mmStack中，这样就大大减少了Heap中pop操作和比较的次数.那么有个问题就是为什么是mm-1，为什么不是mm个呐？？这个问题很好解释。因为我们首先从heap获取候选集，然后再和mmStack求交。一种比较坏的情况是如果把mmStack数组长度设置成mm（也就是MinShouldMatch的值），那么就很有可能一些符合条件的docid全部落在了mmStack中。那么这样你再先从heap中获取候选docid，然后在和mmStack求交就没有结果了。所以最大化的mmStack长度为minShoudlMatch - 1.

3、再和mmStack求交时，对mmStack中Scorer是从短到长遍历，好处是，一旦剩下的Scorer数+当前minShoudlMatch 小于给定条件的话就跳出了，不用再比较剩下list较长的Scorer了。

具体的讨论过程和性能测试参见：

https://issues.apache.org/jira/browse/LUCENE-4571