【中途相遇+二进制】【NEERC 2003】Jurassic Remains
例题25 侏罗纪(Jurassic Remains, NEERC 2003, LA 2965)
给定n个大写字母组成的字符串。选择尽量多的串,使得每个大写字母都能出现偶数次。
【输入格式】
输入包含多组数据。每组数据的第一行为正整数n(1≤n≤24),以下n行每行包含一个大写字母组成的字符串。
【输出格式】
对于每组数据,第一行输出整数k,即字符串个数的最大值。第二行按照从小到大的顺序输出选中的k个字符串的编号(字符串按照输入顺序编号为1~n)。
【样例输入】
6
ABD
EG
GE
ABE
AC
BCD
【样例输出】
5
1 2 3 5 6
直接贴题解吧
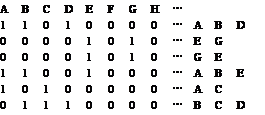
在一个字符串中,每个字符出现的次数本身是无关紧要的,重要的只是这些次数的奇偶性,因此想到用一个二进制的位表示一个字母(1表示出现奇数次,0表示出现偶数次)。比如样例的6个数,写成二进制后如图1-34所示。
图 1-34
此时,问题转化为求尽量多的数,使得它们的xor(异或)值为0。
最容易想到的方法是直接穷举,时间复杂度为O(2n),有些偏大。注意到xor值为0的两个整数必须完全相等,我们可以把字符串分成两个部分:首先计算前n/2个字符串所能得到的所有xor值,并将其保存到一个映射S(xor值à前n/2个字符串的一个子集)中;然后枚举后n/2个字符串所能得到的所有xor值,并每次都在S中查找。
如果映射用STL的map实现,总时间复杂度为O(2n/2logn),即O(1.44nlogn),比第一种方法好了很多。这样的策略称为中途相遇法(Meet-in-the-Middle)。密码学中著名的中途相遇攻击(Meet-in-the-Middle attack)就是基于这个原理。
#include<cstdio>
#include<map>
using namespace std;
const int maxn = 24;
map<int,int> table;
int bitcount(int x) { return x == 0 ? 0 :bitcount(x/2) + (x&1); }
int main() {
int n,A[maxn];
chars[1000];
while(scanf("%d", &n) == 1 && n) {
//输入并计算每个字符串对应的位向量
for(int i= 0; i < n; i++) {
scanf("%s", s);
A[i] =0;
for(intj = 0; s[j] != '\0'; j++) A[i] ^= (1<<(s[j]-'A'));
}
//计算前n1个元素的所有子集的xor值
//table[x]保存的是xor值为x的,bitcount尽量大的子集
table.clear();
int n1 =n/2, n2 = n-n1;
for(int i= 0; i < (1<<n1); i++) {
int x =0;
for(intj = 0; j < n1; j++) if(i & (1<<j)) x ^= A[j];
if(!table.count(x) || bitcount(table[x]) < bitcount(i)) table[x] = i;
}
//枚举后n2个元素的所有子集,并在table中查找
int ans =0;
for(int i= 0; i < (1<<n2); i++) {
int x =0;
for(intj = 0; j < n2; j++) if(i & (1<<j)) x ^= A[n1+j];
if(table.count(x)&&bitcount(ans)<bitcount(table[x])+bitcount(i))ans = (i<<n1)^table[x];
}
//输出结果
printf("%d\n", bitcount(ans));
for(int i= 0; i < n; i++) if(ans & (1<<i)) printf("%d ", i+1);
printf("\n");
}
return 0;
}
几个位运算以及STL巧妙运用注意注意
int bitcount(int x) //计算一串数的二进制还有的1的个数
table.count(x)//判断x是否为控
ans = (i<<n1)^table[x];//合并i与x 两个二进制代表的集合