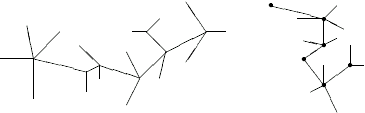
Caterpillar Problem

 

A.    Caterpillar Time Limit: 0.5 Seconds    Memory Limit: 65536K

 

An undirected graph is called a caterpillar if it is connected, has no cycles, and there is a path in the graph where every node is either on this path or a neighbor of a node on the path. This path is called the spine of the caterpillar and the spine may not be unique. You are simply going to check graphs to see if they are caterpillars.

For example, the left graph below is not a caterpillar, but the right graph is. One possible spine is shown by dots.

 

Input

There will be multiple test cases. Each test case starts with a line containing n indicating the number of nodes, numbered 1 through n (a value of n = 0 indicates end-of-input). The next line will contain an integer e indicating the number of edges. Starting on the following line will be e pairs n₁ n₂ indicating an undirected edge between nodes n₁ and n₂. This information may span multiple lines. You may assume that n ≤ 100 and e ≤ 300. Do not assume that the graphs in the test cases are connected or acyclic.

 

Output

For each test case generate one line of output. This line should either be

 

Graph  g  is a caterpillar.

or

 

Graph  g  is not a caterpillar.

as appropriate, where g is the number of the graph, starting at 1.

 

Sample Input

22
21
1 2 2 3 2 4 2 5 2 6 6 7 6 10 10 8 9 10 10 12 11 12 12 13 12 17
18 17 15 17 15 14 16 15 17 20 20 21 20 22 20 19
16
15
1 2 2 3 5 2 4 2 2 6 6 7 6 8 6 9 9 10 10 12 10 11 10 14 10 13 13 16 13 15
0

 

Sample Output

Graph 1 is not a caterpillar.
Graph 2 is a caterpillar.

Source:  East Central North America 2006

 

#include <cstdlib> #include <iostream> #include <vector> using namespace std; int const MAX_N = 105; int const MAX_E = 301; typedef struct _NODE { int count; vector<int> list; _NODE() : count(0), list(vector<int>()){}; }NODE; int main(int argc, char *argv[]) { int n, e; int ID = 1; //freopen("input.txt", "rt", stdin); //freopen("output.txt", "wt", stdout); while( cin >> n, n != 0) { cin >> e; int start, end; int tempE = e; int index = 0; int flag = 0; vector<NODE> vec(MAX_N); while(tempE-- > 0) { cin >> start >> end; vec[start].count++; vec[start].list.push_back(end); vec[end].count++; vec[end].list.push_back(start); } if(n - 1 != e) { cout << "Graph " << ID << " is not a caterpillar." << endl; ID++; continue; } vector<NODE>::iterator it = vec.begin(); vector<NODE>::iterator end1 = vec.begin() + e; for(; it != end1; it++) { int count = 0; if(it->count > 1) { vector<int>::iterator eachIt = (it->list).begin(); vector<int>::iterator eachEnd = (it->list).end(); for(; eachIt != eachEnd; eachIt++) { if(vec[*eachIt].count > 1) count++; } } if(count > 2) { cout << "Graph " << ID << " is not a caterpillar." << endl; flag = 1; break; } } if(!flag) cout << "Graph " << ID << " is a caterpillar." << endl; ID++; } return EXIT_SUCCESS; } 

思路： 如果一个节点有两条或两条以上的边， 就把这个节点看做骨干节点， 要找到这样一条spine， 只要保证每个骨干节点最多和两外两个骨干节点相连即可， 需要两次遍历 ， 第一次遍历用于初始化每个节点的相关信息（与他相连的节点数和这些节点的ID)， 第二遍遍历和每个骨干节点相连的其他骨干节点数， 一旦发现有>2的， 程序结束， 输出NOT...