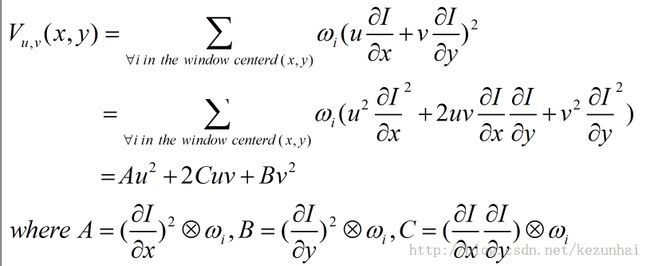图像处理特征不变算子系列之Harris算子(二)
论文转载请注明出处:http://blog.csdn.net/kezunhai
在前面的博文中,介绍了Moravec算子,并对moravec算子的不足也进行了简单的描述,具体请参考:图像处理特征算子系列之Moravec算子(一)。Harris算子针对Moravec算子的不足,提出了以下的改进:
1)Moravec算子各向异性响应(Anisotropic Response of Operator)
Moravec算子仅仅在8个方向(水平、垂直和四个对角方向)计算灰度变化,为了对其扩展,有必要设计一个可以在任何方向对灰度变化进行测度的函数。1988年,Harris和Stephen通过对Moravec算子进行展开,推导得到了Plessey算子,也即Harris算子。
我们先来看看与Harris相关的背景知识。通常,Prewitt算子被用来对图像的梯度进行近似。然而,在实际应用中,一阶梯度通过下图中的公式来进行近似:
对Morevec算子(如果对Moravec算子也不清楚的地方,请参考博主前一篇对Morevec算子的讲解)进行分析可以得到:Two Morevec windows中对应像素差的和可以作为图像梯度的合理近似。我们再来看下图:
通过对上图的分析,我们有可以进一步得到:morevec算子中的灰度变化可以采用图像梯度进行近似。
通过上面的分析,灰度的变化可以表示为图像梯度的函数,公式表示如下:
其中,(u,v)表示滑动,x方向为(1,0),y方向为(0,1),微分的计算如上图所示。
到这里,大家非常明了:上式可以对moravec算子中的灰度变化计算进行精确的逼近。但是又与Moravec算子中灰度变化不同的是通过合理的选择(u,v)可以对任何方向的灰度变化进行测度。
2)噪声响应 (Noise Response)
在Moravec算子中,滑动窗采用的是方形的(square window),方形窗使得不同方向上的中心像素与边界像素的欧式距离是变化的。为了克服这个问题,Harris&Stephen提出只需将方向窗改成圆窗(circle window)。同时,窗中的每个像素是同等地位的,理论上应该是离中心越近的权重越大,而离中心越远,权重越小,因此我们加入高斯权重。因此,灰度变化的新测度方式可以通过下图来表示:
通过公式表示如下:
其中,wi表示位置i处的高斯权重。
3)边缘的强响应(Large Response of Edge)
因为Moravec算子在边缘处很容易出现误检,Harris&Stephen通过考虑不同方向的灰度度量形成新的角度性测度(cornerness measure)。接着,我们对上面的式子进行变换,如下式:
Harris&Stephen同时也注意到,上式可以写成:
对上面的矩阵M,其特征值与图像表面的主曲率是成正比的,并且形成了对M的旋转不变的描述(Proportional to the principle curvature of the image surface and form a rotationally invariant description of M)。然后,由于M是通过水平和垂直方向的梯度来近似的,他们不是真正的旋转不变。
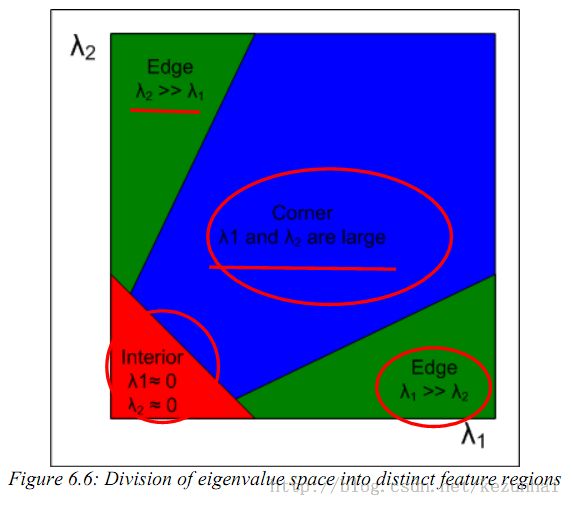
同样,与Moravec算子一样,我们再来看下面的四张张图:
图中A表示在一个物体的内部或背景上,窗口内的灰度值相对不变,因此该窗口表面上几乎没有曲率,因此M的特征值相对很小;B窗口在一个边缘处,垂直于边缘的地方将有明显很大的曲率,而平行于边缘的地方几乎没什么曲率,因此该形式下M的特征值一个会比较大,另一个较小;C和D对应于角度和离散点,在两个方向都会有很大的曲率,因此,M的特征值都将会很大。假设r1和r2是M的两个特征值,通过上面的分析,可以将一个平面表示为以下三个可区分的区域:
Harris&Stephen提出下面的角点性测度(cornerness measure)
:
k一般取值04~0.6。
最后,我们来总结下Harris算子的计算步骤:
( 1)对每一个像素计算自相关矩阵M
(2)构造角点性映射图(Construct cornerness map)
(3)阈值化,对得到的C(x,y)进行阈值
(4)非极大值抑制
总结:Harris算子针对Moravec算子的不足进行了改进,提高了特征点的检测率以及Repeatability。但是,Harris算子计算量大,对尺度很敏感,不具有尺度不变形;另外Harris对特征点的定位也不是很精确,而且Harris也是各向异性的,对噪声敏感。