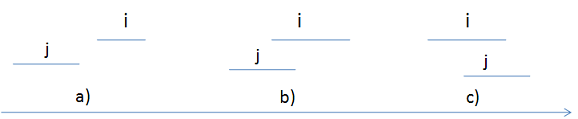算法导论7.6对区间的模糊排序

题目：

7-6 对区间的模糊排序

    考虑这样的一种排序问题，即无法准确地知道待排序的各个数字到底是多少。对于其中的每个数字，我们只知道它落在实轴上的某个区间。亦即，给定的是n个形如[ai,bi]的闭区间，其中ai≤bi。算法的目标是对这些区间进行模糊排序(fuzzy-sort)，亦即，产生的各区间的一个排列<i1,i2,...,in>，使得存在一个cj∈[ai, bi]，满足c1≤c2≤...≤cn。

a）为n个区间的模糊排序设计一个算法。你的算法应该具有算法的一般结构，它可以快速排序左部端点（即各ai），也要能充分利用重叠区间来改善运行时间。（随着各区间重叠得越来越多，对各个区间进行模糊排序的问题会变得越来越容易。你的算法应能充分利用这种重叠。）

b）证明：在一般情况下，你的算法的期望运行时间为Θ(nlgn)，但当所有的区间都重叠时，期望的运行时间为Θ(n)（亦即，当存在一个值x，使得对所有的i，都有x∈[ai,bi]）。你的算法不应显示地检查这种情况，而是应当随着重叠量的增加，性能自然地有所改善。

思路：

刚开始看到这个题目，整了半天没整明白是个什么回事，后来通过例子终于自我认为理解了。要理解上面所说的区间模糊排序。首先要点是，这是区间排序，即和快速排序不同，快速排序是每一个元素都是确定的，而这里每一个元素都是一段区间，排序结果也是不一定正确的，即是模糊的。要先理解下面的一个偏序关系

  先思考一个问题：为什么区间重叠能改善排序算法的期望运行时间呢？想明白了其实很简单，这相当于我们用快速排序一个数组时，数组中有很多重复元素，如果我们做一个改进，将划分从2部分变成3部分，前边部分是小于，中间是等于，后面是大于。那么以后每次需要划分的区间（只划分小于和大于）都可能会大大减小，这样PARTITION时就可能非常高效。

a）首先定义两个线段的偏序关系(非唯一)，如下图所示

以线段i的左端点ai为参照物，分为三种情况：

1）线段j<线段i， 此时满足b.end<a.begin

2）线段j=线段i， 此时满足b.begin≤a.begin≤b.end。这样定义的原因是：最后可以让线段j和线段i的ci均取a.begin（重叠部分）

3）线段j>线段i， 此时满足b.begin>a.begin

通过上图我们可以清晰地感性地认知偏序小于，偏序大于，偏序等于各属于什么情况。图真是一个好东西

思考很久，我终于发现区间模糊排序本质上是快排的一种变种。

区间排序实质上是以区间为单位进行操作，所以，需要定义一个结构体保存区间首尾元素。而快排是以元素为单位排序。

通过定义偏序大于，小于和等于关系，再对快排的partition做了一点改进，使它每次都可以返回一个区间结构体，使得左边的小于，右边的大于，中间的等于。

代码：

#include<iostream>
#include<ctime>
using namespace std;
//模糊排序的输入是一个区间数值对，所以定义一个结构体
struct node
{
	int a;
	int b;
};
//交换两个结构体
void swap(node& a,node& b)
{
	node temp=a;
	a=b;
	b=temp;
}
//划分成三段的partition函数，最左边是小于主元，最右边是大于主元，中间是等于主元的
//将区间[l,r]以某区间为基准，分成[l,i]<[i+1,j-1]<[j,r]三个区间
node partition(node a[],int l,int r)
{
	//选最后一个元素为主元，ret为保存划分点的结构体
	node x=a[r],ret;
	int i=l-1;//跟踪小区间
	int j=r+1;//跟踪大区间
	int k=l;//遍历整个数组
	while(k<j && k<=r)
	{
		if(a[k].b<x.a)	//如果小于主元，交换到前面  
		{
			++i;
			swap(a[i],a[k]);
			++k;
		}
		else if(a[k].a>x.a) ////如果大于，交换到后面  
		{
			j--;
			swap(a[j],a[k]);//这里不能k++，因为交换过来的元素也可能大于主元  
		}
		else 
		{//两个区间有重叠，视作相等，取它们重叠的部分作为基准区间继续划分，一开始基准区间比较大，划分到后面，基准区间渐渐变小
			//划分到最后的结果就是[i,j]，则i的左边是小区间，j的后边是大区间，而[i,j]是剩余区间重叠的部分，即相等的部分
			//本质上是快速排序的变种，快排是每调用partition一次，可以确定一个枢点，使其左边的数小于枢点，右边的数大于枢点
			//而这个每调用partition一次，可以确定一个“相等”区间，使其左边的都小于（偏序意义上）枢点区间，右边大于枢点区间
			//快排可以确定一个准确序列，而模糊化排序可以确定一个可能的区间排序
			x.a=max(a[k].a,x.a);
			x.b=min(a[k].b,x.b); //如果相等，不交换，但是要提取公因子
			++k;
		}
	}
	ret.a=i;
	ret.b=j;
	return ret;//ret暂存作用
}

void Fuzzy_sort(node a[],int l,int r)
{
	if(l<r)
	{
		node mid=partition(a,l,r);//mid保存分割点[i,j]
		//中间重叠部分不处理，只处理两头部分
		Fuzzy_sort(a,l,mid.a);
		Fuzzy_sort(a,mid.b,r);
	}
}
bool print_possible_sort(node a[],int n)
{
	int* c=new int[n];
	c[0]=a[0].a;
	cout<<c[0]<<' ';
	for(int i=1;i<n;i++)
	{
		c[i]=max(a[i].a,c[i-1]);
		if(c[i]>a[i].b)//出错的情况为第i个区间比第i+1个区间大，即i.a>(i+1).b
		{
			cout<<"error!"<<endl;
			return false;
		}
		cout<<c[i]<<' ';
	}
	delete []c;
	return true;
}
int main()
{
	srand((unsigned)time(0));
	node a[10000];
	int n=0;
	cout<<"输入区间个数n:";
	cin>>n;
	cout<<"下面随机输入"<<n<<"个区间的起点终点a,b:"<<endl;
	for(int i=0;i<n;i++)//产生有效区间对
	{
		a[i].a=rand()%1000;
		a[i].b=rand()%1000;
		if(a[i].a>a[i].b)
		{
			swap(a[i].b,a[i].a);
		}
		cout<<a[i].a<<" "<<a[i].b<<endl;
	}
	Fuzzy_sort(a,0,n-1);
	cout<<"模糊排序的结果如下："<<endl;
	for(int i=0;i<n;i++)
		cout<<a[i].a<<" "<<a[i].b<<endl;
	cout<<"可能存在的排列如下："<<endl;
	if(print_possible_sort(a,n))
	{
		cout<<endl<<"成功找到一个满足条件的排列。"<<endl;
	}
	else
	{
		cout<<"算法失败！"<<endl;
	}
	return 0;
}