神奇的舞蹈~~Dancing_Links

神奇的舞蹈~~Dancing_Links

整了一天的跳舞链，资料可以在网上搜到
http://sqybi.com/works/dlxcn/
惊讶于它做深搜的时候可以达到如此强劲的剪枝
下午的时候不看网上的模板自己写了一个，自认为是比模板少了一个for循环，但是写好后才发现没有模板的启发式搜索的效率，就这样活生生的TLE了，浪费了我好几个小时啊~~%>_<%~~
晚上只好写用模板的方法，写了一个后瞬间过了，感觉难度也不过尔尔
但这个舞蹈链可是容易解答却很难看出的主，构造舞蹈链还是关键
献上我的模板~~
最简单的舞蹈链，效率仅比hhanger差，可以跑240MS,不过后来我测出了一些数据的结构，暴力优化到了124MS，哈哈哈(得意一下)~~~
http://acm.hust.edu.cn/thanks/problem.php?id=1017
(精确覆盖问题)

void  remove( int   & c) {
    L[R[c]]  =  L[c];
    R[L[c]]  =  R[c];
     for ( int  i  =  D[c]; i  !=  c ; i  =  D[i]) {
         for ( int  j  =  R[i]; j  !=  i ; j  =  R[j]) {
            U[D[j]]  =  U[j];
            D[U[j]]  =  D[j];
             -- S[Col[j]];
        }
    }
}
void  resume( int   & c) {
     for ( int  i  =  U[c];i  !=  c;i  =  U[i]) {
         for ( int  j  =  L[i]; j  !=  i ; j  =  L[j]) {
             ++ S[Col[j]];
            U[D[j]]  =  j;
            D[U[j]]  =  j;
        }
    }
    L[R[c]]  =  c;
    R[L[c]]  =  c;
}
bool  dfs() {
     if (R[ 0 ]  ==   0 ) {
         return   true ;
    }
     int  i , j;
     int  idx,minnum  =   999999 ;
     for (i  =  R[ 0 ];i  !=   0  ; i  =  R[i]) {
         if (S[i]  <  minnum) {
            minnum  =  S[i];
            idx  =  i;
        }
    }
    remove(idx);
     for (i  =  D[idx]; i  !=  idx; i  =  D[i]) {
        ans[deep ++ ]  =  Row[i];
         for (j  =  R[i]; j  !=  i ; j  =  R[j]) {
            remove(Col[j]);
        }
         if (dfs()) {
             return   true ;
        }
        deep  -- ;
         for (j  =  L[i]; j  !=  i ; j  =  L[j]) {
            resume(Col[j]);
        }
    }
    resume(idx);
     return   false ;
}

http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemCode=3209
(精确覆盖问题)
浙大的这道省赛题其实就是完美覆盖的转化~把每一格都分开来，要求就是选N个方块把图完美覆盖全部搜完然后最小的个数
思路：行方块，列单位小格子，矩阵中1是方块所能覆盖的小格子

http://acm.nuaa.edu.cn/acmhome/problemdetail.do?&method=showdetail&id=1507 
(重复覆盖问题) 重复覆盖的模板题
献上模板

void remove(int &c) {
    for(int i = D[c]; i != c ; i = D[i]) {
        L[R[i]] = L[i];
        R[L[i]] = R[i];
    }
}
void resume(int &c) {
    for(int i = U[c]; i != c ; i = U[i]) {
        L[R[i]] = i;
        R[L[i]] = i;
    }
}
int h() {
    bool hash[51];
    memset(hash,false,sizeof(hash));
    int ret = 0;
    for(int c = R[0]; c != 0 ; c = R[c]) {
        if(!hash[c]) {
            ret ++;
            hash[c] = true;
            for(int i = D[c] ; i != c ; i = D[i]) {
                for(int j = R[i] ; j != i ; j = R[j]) {
                    hash[Col[j]] = true;
                }
            }
        }
    }
    return ret;
}
bool dfs(int deep,int lim) {
    if(deep + h() > lim) {
        return false;
    }
    if(R[0] == 0) {
        return true;
    }
    int idx , i , j , minnum = 99999;
    for(i = R[0] ; i != 0 ; i = R[i]) {
        if(S[i] < minnum) {
            minnum = S[i];
            idx = i;
        }
    }
    for(i = D[idx]; i != idx; i = D[i]) {
        remove(i);
        for(j = R[i]; j != i ; j = R[j]) {
            remove(j);
        }
        if(dfs(deep+1,lim)) {
            return true;
        }
        for(j = L[i]; j != i ; j = L[j]) {
            resume(j);
        }
        resume(i);
    }
    return false;
}

http://acm.tju.edu.cn/acm/showp3219.html  
http://acm.hdu.edu.cn/showproblem.php?pid=2295
(重复覆盖问题)
这题无法转化成完美覆盖，所以remove和resume的时候要变化一下，但是这样还是会超时我看了标程才算AC。唉。。
主要是里边的一个A*的h函数是在是太犀利了，一下从TLE到了46MS。。。。剪枝还是非常重要的
思路：行是雷达，列是城市，矩阵中1是雷达覆盖城市

http://acm.fzu.edu.cn/problem.php?pid=1686  
(重复覆盖问题)
这道题也同上道一样是："在0-1矩阵中选取最少的行，使得每一列最少有一个1" 这个模型
所以和上一道建表一样建好之后套上模板就AC了~
思路：行是枚举在每个位子放魔法，列式怪物个数(最好给怪物标记个id)，矩阵中的1是在这个地方放魔法是否能达到目标怪物

http://www.spoj.pl/problems/NQUEEN/
(重复覆盖问题)
N皇后问题，打的时候没能想到怎么转化成精确覆盖，只是用了dancing links的思想，傻傻的花了一个晚上完成了一个超级复杂的米字型链表(重复覆盖)，开始的时候启发式函数S没有更新，导致没有发挥效用，结果本例30个0的数据都跑不出来，还以为是想法出错了，睡觉前在床上想到，改了一下，效率呈指数级增长，50个0的瞬间跑出来，在state里排到第一，哈哈

(精确覆盖问题)
今天CH教我怎么将之转化成十字链表的精确覆盖，但是矩阵是(n*n)*(6*n-2)比米字型链表n*n的大了好多倍，交了一下，跑了1s，效率不如米字型的
其思路是：行是格子数n*n,列是(行+列+正逆对角线)，矩阵中的1是放在各自上所占得行，列，对角线
不需要全部搜完，只要初始皇后+dfs的深度达到n(放了n个皇后)就return true

http://acm.hdu.edu.cn/showproblem.php?pid=2828 
(精确覆盖问题) 
这题恶化N皇后一样可以转化成多种覆盖。我是精确覆盖，列是n+m只要精确前n个就够了
(重复覆盖问题) 
还可以转化成不精确，那么列就是n

当然，此题出题人的意图是二分匹配。。。

http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemId=31
http://acm.pku.edu.cn/JudgeOnline/problem?id=1084
(重复覆盖问题)
这题要不和我说是dancing links 我还真看不出来
此题建表超烦，虽看出来但是建表就花了我一个半小时，还迫我使用上行的头节点，以前我只是用列的头节点，努力了很久，过了sample就AC了，烦就烦在建表上
思路：行是火柴棒数，列是完美时能构成的矩阵数目，矩阵中的1是列矩阵是否包含行火柴

http://acm.pku.edu.cn/JudgeOnline/problem?id=3074
http://acm.pku.edu.cn/JudgeOnline/problem?id=3076
http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemId=3038
(精确覆盖问题)
经典的数独，看了论文才明白怎么覆盖，9*9*9的行 (9+9+9)*9+9*9的列
思路：行是81个小格*每个格子的9个可能数字，列是81个小格+9行9列9小块的9个数字
每列确切的有4个1
开始读入的时候吧确定的数字的头上的1删掉可以很大的提高效率

http://acm.hdu.edu.cn/showproblem.php?pid=2518 
超爽的dancing links
这题所有的方块可以旋转，这点超烦~
我差点就人肉代码了，枚举所有状态，不过最后我还是修改成不人肉的办法
只有几组答案，用dancing links暴力跑出所有组合后然后打表，嘿嘿，我就是这么猥琐的过的
72*所有摆放数~
思路：60个格子加12个方块作为列，所有摆放的方案数作为行


好了，A光上述题目dancing links的学习也告一段落，这个舞蹈是在是优美，以后出题一定要谱一曲经典的舞蹈~~



2009.9.6
发现dancing links还能做 最大团
http://acm.hdu.edu.cn/showproblem.php?pid=1530
转化成补图后再建表。。。不过效率很低，跑了6000+MS，全部搜完找一个最大的，还没有更优的办法优化，尝试过二分再写个h函数未果。。。

10.15
http://acm.hdu.edu.cn/showproblem.php?pid=3156

和雷达类似，不过放radar的点要求出来，也是先二分枚举半径，然后利用两个点和半径确定一个圆心C(n,2)，可以证明如果放其他地方一定没这个圆心优

Dancing Links 算法学习小结

LBoy posted @ 2011年2月27日 02:29 in  Algorithm Study with tags  Dancing Links , 1800 阅读

文中提及的一些观点和理论，并非全部个人原创，而是自己的总结和心得， 仅供个人学习编程使用！

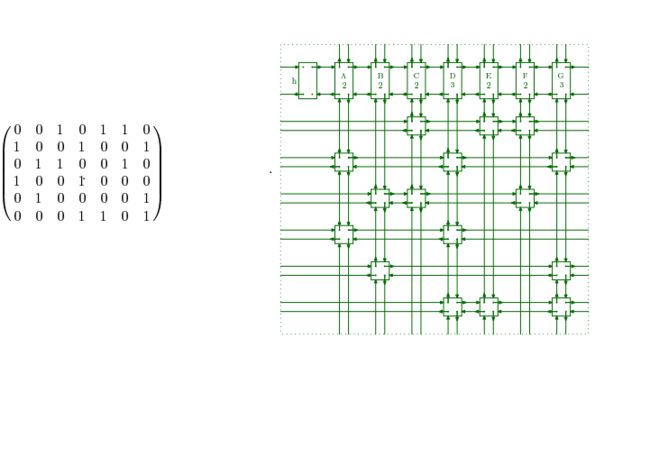
Dancing Links（DLX），又 被直译为“神奇的舞蹈链”，本质是一个“双向十字循环链表”！是由斯坦福大学的康纳德 E.Knuth在2000年左右提出的一个解决一种NPC问题的算法！对我们acm的竞赛来说，在处理一类搜索问题时，十分有用。

先分享一下学习这种算法比较好的几份资料：

1. 《Dancing Links》 （Donald E. Knuth）本人的论文。英文版的，也有中文的，而且翻译的也很到位: http://sqybi.com/works/dlxcn/#p11#p11

2.《Dancing Links在搜索中的应用》 （momodi）momodi的这篇文章比较系统的讲述了dlx的原理及处理Exact Cover Problem 和 重复覆盖的方法。

依据做过的题目的特点，在简单描述过dlx的插入和删除的方法之后，结合相应的题目，讲一下自己对“完美覆盖（棋盘问题，数独（sudoku）问题，N皇后问题）” 和 “重复覆盖”的理解。

dlx的节点的存储结构：用结构体来表示：

struct node {
    int S, C;      // size->列链表中节点的总数; column-> 列链表头指针；
    int L, R;      // left->左向指针， right-> 右向指针; 左右方向
    int U, D;      // up-> 上向指针， down-> 下向指针；上下方向
};

dlx的节点的删除

dlx的节点的删除

dlx的节点的恢复

dlx的节点的删除

除此之外，为了遍历的方便，要设置一个总的头节点的head!

完美覆盖（精确覆盖）模型

给定一个0-1矩阵，现在要选择一些行，使得一列有且仅有一个 1，如下左：

取行集合｛1， 4， 5｝便可以使得每一列仅有一个1。如果我们把行集合｛2， 3， 6｝删掉，并用不同的染色将剩余的行中列为1的标记出来，那么就会得到一个一个完全覆盖的board。这也是这个题目的算法的大体思路：任意选择一列（这里我们先选择任意一列，待会再说如何优化），选择为1的一行，然后将该从该行中找出所有的节点值为1的节点，将这些节点所在的列中节点为值为1的行删除掉，这样我们就可以保证选择了改行之后，保证每列中只有一个1。 这样将所有的行试探之后，如果最后存在一种可以使得原矩阵为空的方案，那么就找到一组解。下面简单说一下对优化（即，每次选择剩余列中元素个数最少的来删除）的理解，

我们优化的出发点是选择尽量少的行找到一组可行解，按照我们上面的思路就是选择一行的同时尽量多的删除其它的行。由此，列的值（多少代表着影响的行数）大的删掉的行数也就越多，那么就更大的可能接近可行解。（只是论述，缺乏严密的数学证明）（更为具体的分析，参见momodi的论文P4，下面附上一段伪代码,帮助理解）

0-1 matrix exact cover problem

完美覆盖的cpp实现。

0-1 matrix exact cover problem the implemention with cpp

重复覆盖模型：在0-1矩阵中选择最少的行，是的每一列至少有一个1.

该问题可以想象成二分图的支配集问题的模型：从X集合选择最少的点，是的能否覆盖住Y集合所有的点。（当然X与Y集合是有边（映射）关系的）。

把这个问题和上面的完美覆盖结合起来看，我们就会发现不同的地方就是，上面红色标出的那句话，实际上也是如此。能够想到的一个中直观的搜索方法是：我们每次选择任意选一列，然后从该列选择任意一行，同时将列值为1的节点所在的列删掉（这里不再是将列上值为1的节点所在的行删掉，因为不再要求列值为1）。如果，最后的所有的列都删掉了，那么就可以说找到一组可行解。

这个题目的做法是用迭代加深的启发式搜索（ID_A*)。那么，我们来说一下启发函数的设计。

启发函数H()

启发函数的值 = 按一定的规则选择列，是的所有的列都被选择需要的最少的行数。（这里的按一定的规则是说，每次开始选择列的时候都遵守一个规则）。说明估价函数（f() = g() + h()）发函数的正确性,我们只需要说明两点：1. f（）满足单调不减的特性； 2. h()是相容的，也就是说,设pres, curs 为前一个状态和当前状态，weight为状态转移代价，那么h(pres) <= curs + weight。 按通常的dfs的估价函数设计的方法，去实际代价函数g（） = depth of the search. 那么 g()函数值每只增加一个单位“1”。对于h()函数，按照f的不递减的特性，需要满足每次减少的最大值为“1"才可。 如果按照我们我们上面启发函数的设计原则，每次计算的时候记录下计算估价函数值时用到的列，那么，对于当前的此次计算挂架函数值，会出现两种情况，一是，原来记录下的列有被删除的（每次只能删除一个原来记录的列，因为，记录的列之间是没有关系的），这样h（）的函数值减小一；二是，原来记录的列没有被删除的，这样h()的函数值保持不变。由此，weight = 0 或 1，h() 函数是相容的，f() = g() + h() 满足单调不递减的特性。 

 简单的来说，对于重复覆盖，我们只删除列，不删除行。由此得到以下的cpp重复覆盖的代码（供参考）

重复覆盖的cpp implementation

 对于ID_A*,我个人比较喜欢下面的这种实现方法：

重复覆盖的cpp implementation

 

 

hdu3498whosyourdaddy(DLX+A*解重复覆盖问题)

分类： DLX 2013-09-18 21:25  142人阅读  评论(2)  收藏  举报

DLX

谨以此题，献给中秋夜还在默默刷题的孩纸们。。

题目请戳这里

题目大意：给n个点，m个关系(a,b)，表示点a和点b相邻。每个点最多4个相邻点。现在如果消灭某个点，就可以同时消灭与之相邻的点。现在问最少要消灭几个点，能使每个点都至少被消灭一次。

题目分析：最小点支配集的求解。NP难问题。好在数据规模不大，搜索可以解决。不过要用dancing links+A*优化。

重复覆盖和精确覆盖的区别仅仅是选中一列后只删除这一列即可，不用像精确覆盖那样先删掉所有覆盖这列的行，再删除这些行能覆盖的列保证每列只覆盖一次。

另外要加一个启发函数剪枝。关于这个剪枝函数，就是估计在当前局面下，最少还要几行才能覆盖所有剩下的列。因此这是一个估计上界。具体做法与精确覆盖的删除操作比较像。先选中未被删除的一列，删除覆盖该列的所有行，同时删除这些行覆盖的所有列。由此估计出覆盖剩余列需要的行数的上界。

详情请见代码：

 #include <iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 using namespace std;
 const int N = 60;
 const int M = 360;
 const int inf = 0x3f3f3f3f;

 bool flag[N][N];
 int n,m,num,ans;
 int u[M],d[M],l[M],r[M],row[M],col[M],s[M],h[M];

 void init()
 {
     memset(h,0,sizeof(h));
     memset(s,0,sizeof(s));
     int i;
     for(i = 0;i <= n;i ++)
     {
         u[i] = d[i] = i;
         r[i] = (i + 1) % (n + 1);
         l[i] = (i - 1 + n + 1) % (n + 1);
     }
     num = n + 1;
 }
 void build(int i,int j)
 {
     if(h[i])
     {
         r[num] = h[i];
         l[num] = l[h[i]];
         r[l[num]] = num;
         l[r[num]] = num;
     }
     else
     {
         h[i] = num;
         l[num] = r[num] = num;
     }
     s[j] ++;
     u[num] = u[j];
     d[num] = j;
     d[u[num]] = num;
     u[j] = num;
     col[num] = j;
     row[num] = i;
     num ++;
 }
 void remove(int x)
 {
     for(int i = d[x];i != x;i = d[i])
         l[r[i]] = l[i],r[l[i]] = r[i],s[col[i]] --;
 }
 void resume(int x)
 {
     for(int i = u[x];i != x;i = u[i])
         l[r[i]] = r[l[i]] = i,s[col[i]] ++;
 }
 int A()
 {
     int ret = 0;
     int i,j,k;
     bool vis[N];
     memset(vis,false,sizeof(vis));
     for(i = r[0];i;i = r[i])
     {
         if(vis[i] == false)
         {
             vis[i] = true;
             ret ++;
             for(j = d[i];j != i;j = d[j])
                 for(k = r[j];k != j;k = r[k])
                     vis[col[k]] = true;
         }
     }
     return ret;
 }
 void dfs(int dp)
 {
     if(dp + A() >= ans)//少个等号就TLE...
         return;
     int i,j;
     if(r[0] == 0)
     {
         ans = min(ans,dp);
         return;
     }
     int Max = inf;
     int maxcol;
     for(i = r[0];i;i = r[i])
     {
         if(s[i] < Max)
         {
             Max = s[i];
             maxcol = i;
         }
     }
     for(i = d[maxcol];i != maxcol;i = d[i])
     {
         remove(i);
         for(j = r[i];j != i;j = r[j])
         {
             remove(j);
             s[col[j]] --;
         }
         dfs(dp + 1);
         for(j = l[i];j != i;j = l[j])
         {
             resume(j);
             s[col[j]] ++;
         }
         resume(i);
     }
 }

 int main()
 {
     int i,j;
     while(scanf("%d",&n) != EOF)
     {
         scanf("%d",&m);
         memset(flag,false,sizeof(flag));
         while(m --)
         {
             scanf("%d%d",&i,&j);
             flag[i][j] = true;//= flag[j][i]
         }
         init();
         for(i = 1;i <= n;i ++)
             for(j = 1;j <= n;j ++)
                 if(flag[i][j] || i == j)//i == j!!!
                     build(i,j);
         ans = inf;
         dfs(0);
         printf("%d\n",ans);
     }
     return 0;
 }

慢的不忍直视。。。。

POJ3740Easy Finding(DLX入门)

分类： DLX 数据结构 2013-05-31 23:12 52人阅读 评论(0) 收藏 举报

DLX 数据结构

->题目请戳这里<-

题目大意：给一个m*n的01矩阵，求是否存在若干行，使这些行中的1覆盖所有的列恰好1次。

题目分析：裸的精确覆盖题目，建图+模版= AC。需要用到dance links这种数据结构优化。dancing links也是最近才学，今天刚弄明白，这此特别感谢yyd大牛，帮我解决了一个小瓶颈。

关于dancing links，仔细研究才能发现dancing lingks是如此绝妙的数据结构，优雅的代码，超高的效率，无不让人惊叹，欢迎进入dancing links的世界：

Knuth原版论文：http://wenku.baidu.com/view/60eb28ded15abe23482f4d77.html

中文翻译：http://wenku.baidu.com/view/d8f13dc45fbfc77da269b126.html

关于本题，详情请见代码：

#include <iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int N = 305;
const int M = 20;
const int MX = N * M;
int m,n;
int head,size;
int s[MX],u[MX],d[MX],l[MX],r[MX],h[MX],col[MX],row[MX];

void init()
{
head = 0;
memset(s,0,sizeof(s));
int i;
for(i = 0;i <= n;i ++)
{
r[i] = (i + 1) % (n + 1);
l[i] = (i - 1 + n + 1) % (n + 1);
u[i] = d[i] = i;
}
size = n + 1;
memset(h,0,sizeof(h));
}

void remove(int c)
{
l[r[c]] = l[c];
r[l[c]] = r[c];
int i,j;
for(i = d[c];i != c;i = d[i])
{
for(j = r[i];j != i;j = r[j])
{
u[d[j]] = u[j];
d[u[j]] = d[j];
s[col[j]] --;
}
}
}

void recover(int c)
{
int i,j;
for(i = u[c];i != c;i = u[i])
{
for(j = l[i];j != i;j = l[j])
{
s[col[j]] ++;
u[d[j]] = d[u[j]] = j;
}
}
l[r[c]] = r[l[c]] = c;
}

void insert(int i,int j)
{
s[j] ++;//第j列增加一个元素
if(h[i])//第i行已经有元素了，h[i]记录第i行第一个元素地址
{
r[size] = h[i];
l[size] = l[h[i]];
l[r[size]] = size;
r[l[size]] = size;
}
else
{
h[i] = size;
l[size] = r[size] = size;
}
u[size] = u[j];
d[size] = j;
d[u[j]] = size;
u[j] = size;
col[size] = j;//该点属于第j列
row[size] = i;//该点属于第i行
size ++;
}

bool dfs(int k)
{
if(head == r[head])
return true;
int mn = MX;
int cur;
int i,j;
for(i = r[head];i != head;i = r[i])
{
if(s[i] < mn)
{
mn = s[i];
cur = i;
}
}
remove(cur);
for(i = d[cur];i != cur;i = d[i])
{
for(j = r[i];j != i;j = r[j])
remove(col[j]);
if(dfs(k + 1))
return true;
for(j = r[i];j != i;j = r[j])
recover(col[j]);
}
recover(cur);
return false;
}

int main()
{
int i,j,t;
while(scanf("%d%d",&m,&n) != EOF)
{
init();//初始化列头
for(i = 1;i <= m;i ++)
{
for(j = 1;j <= n;j ++)
{
scanf("%d",&t);
if(t)
insert(i,j);
}
}
if(dfs(0) == false)
{
printf("It is impossible\n");
}
else
{
printf("Yes, I found it\n");
}
}
return 0;
}
//276K 360MS