ACM-计算几何之The area——hdu1071
The area
题目: http://acm.hdu.edu.cn/showproblem.php?pid=1071
Problem Description
Ignatius bought a land last week, but he didn't know the area of the land because the land is enclosed by a parabola and a straight line. The picture below shows the area. Now given all the intersectant points shows in the picture, can you tell Ignatius the area of the land?
Note: The point P1 in the picture is the vertex of the parabola.
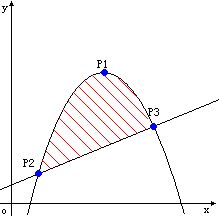
Input
The input contains several test cases. The first line of the input is a single integer T which is the number of test cases. T test cases follow.
Each test case contains three intersectant points which shows in the picture, they are given in the order of P1, P2, P3. Each point is described by two floating-point numbers X and Y(0.0<=X,Y<=1000.0).
Output
For each test case, you should output the area of the land, the result should be rounded to 2 decimal places.
Sample Input
2
5.000000 5.000000
0.000000 0.000000
10.000000 0.000000
10.000000 10.000000
1.000000 1.000000
14.000000 8.222222
Sample Output
33.33
题目: http://acm.hdu.edu.cn/showproblem.php?pid=1071
Problem Description
Ignatius bought a land last week, but he didn't know the area of the land because the land is enclosed by a parabola and a straight line. The picture below shows the area. Now given all the intersectant points shows in the picture, can you tell Ignatius the area of the land?
Note: The point P1 in the picture is the vertex of the parabola.

Input
The input contains several test cases. The first line of the input is a single integer T which is the number of test cases. T test cases follow.
Each test case contains three intersectant points which shows in the picture, they are given in the order of P1, P2, P3. Each point is described by two floating-point numbers X and Y(0.0<=X,Y<=1000.0).
Output
For each test case, you should output the area of the land, the result should be rounded to 2 decimal places.
Sample Input
2
5.000000 5.000000
0.000000 0.000000
10.000000 0.000000
10.000000 10.000000
1.000000 1.000000
14.000000 8.222222
Sample Output
33.33
40.69
依旧是求面积的,给三个点A,B,C
A是抛物线顶点,B、C是直线与抛物线的交点。
求直线与抛物线的面积。。。数学上应该叫定积分,恩。
既可以对"抛物线-直线"求定积分,
也可以对"抛物线"求定积分在减去一个直角梯形的面积。
求抛物线的a,b,c:
x1,y1代表顶点坐标
x2,y2,x3,y3代表剩下两个交点
y2=a*(x1-x2)^2+y1;
-b/2*a=x1;
c=y1-a*x^2-b*x;
我用的第二个方法:
#include <iostream>
#include <stdio.h>
using namespace std;
double a,b,c;
double f(double x)
{
return 1.0/3*a*x*x*x+0.5*b*x*x+c*x;
}
int main()
{
double x1,y1,x2,y2,x3,y3;
int n;
cin>>n;
while(n--)
{
cin>>x1>>y1>>x2>>y2>>x3>>y3;
a=(y2-y1)/((x2-x1)*(x2-x1));
b=-2*a*x1;
c=y1-a*x1*x1-b*x1;
printf("%.2lf\n",f(x3)-f(x2)-(y3+y2)*(x3-x2)/2);
}
return 0;
}