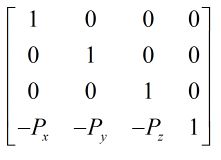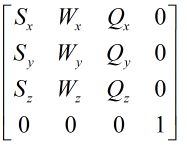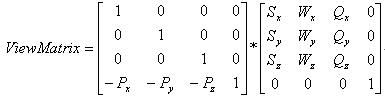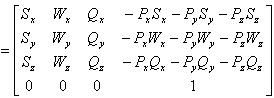view matrix 计算
一、列主序(OPENGL)和行主序(Direct3D)
在计算ViewMatrix之前先讲明列主序(OPENGL)和行主序(Direct3D),搞清楚这个,理解算法程序会很有帮助。
1.矩阵在内存中的存储
不管是D3D还是OpenGL,使用的矩阵都是线性代数标准的矩阵,只是在存储方式上有所不同。分别为:行主序(Direct3D),列主序(OpenGL)
存储顺序说明了线性代数中的矩阵如何在线性的内存数组中存储。例如:内存中使用一个二维数组m存储矩阵,第i行第j列的表示方法分别为:
行主序:m[i][j]
列主序:m[j][i]
线性代数意义的同一个矩阵,在D3D和GL中的存储顺序:
线代: a11,a12,a13,a14 d3d : a11,a12,a13,a14 gl: a11,a21,a31,a41
a21,a22,a23,a24 a21,a22,a23,a24 a12,a22,a32,a42
a31,a32,a33,a34 a31,a32,a33,a34 a13,a23,a33,a43
a41,a42,a43,a44 a41,a42,a43,a44 a14,a24,a34,a44
2.行主序的矩阵与列主序的矩阵如何转换呢?
不难发现,M行=M列的转稚
总结:
OpenGL与Direct3D几点不同(坐标系,向量,绕序):
|
|
OpenGL |
Direct3D |
| 坐标系 |
右手坐标系 |
左手坐标系 |
| 向量 |
列向量 |
行向量 |
| 矩阵存储方式 |
列主序 |
行主序 |
| 多边形正面顶点绕序 |
逆时针 |
顺时针 |
向量的行列性导致矩阵与向量乘法方式有所不同:
列向量 ==> 矩阵右乘向量
行向量 ==> 矩阵左乘向量
其中OpenGL可以设置顺时针为多边形正面顶点绕序。
二、视点矩阵计算:
视点矩阵(view matrix)模拟我们的眼睛或者摄像机。 在流水线(pipeline)中, 视点矩阵将作用于所有顶点.
在进行投影转换时设置的视景体, 决定了我们能在屏幕上看见什么.
在D3D中,
视景体是以坐标原点为视点, 直视Z轴正方向. 所以, 如果希望看到3D空间中不同位置, 不同角度的图像. 就需要将视点转换回坐标原点.
从本质上讲, 所有这些矩阵变换都将作用于顶点. 所以都是模型的变换.
假设视点位于P(Px, Py, Pz)点, 方向为Q(Qx, Qy, Qz), 头顶方向U(Ux, Uy, Uz)根据这些计算视点矩阵.
第一步: 将视点移回原点. 这个矩阵很好计算:
第二步: 建立视点坐标系.
在这里, 我们需要根据Q和U计算出三个互相垂直的单位向量, 用来表示当前的视点坐标系. Q相对于Z轴正方向, W相对于Y轴正方向, S相对于X轴正方向.
第三步: 将XYZ坐标系下的点转换到SWQ坐标系下.
这里需要一些思考, 现在的S(Sx, Sy, Sz), W(Wx, Wy, Wz), Q(Qx, Qy, Qz)都是在XYZ坐标系下表示的向量. XYZ坐标系下的点, 要转换到SWQ坐标系下, 其实并不难. 假设点K(Kx, Ky, Kz)是XYZ坐标系下的点, L是SWQ坐标系下的点:
Lx = Kx * Sx + Ky * Sy + Kz * Sz;
Ly = Kx * Wx + Ky * Wy + Kz * Wz;
Lz = Kx * Qx + Ky * Qy + Kz * Qz;
由此, 我们可以推出转换矩阵:
第四步: 将第一步和第二步的矩阵相乘, 我们就可以得出最终的view矩阵:
在OPENGL中,列主序,视点矩阵为:
实现子程序(OPENGL):
static void buildLookAtMatrix(double eyex, double eyey, double eyez, //
eye position
double centerx, double centery, double centerz,
// view center:(0, 0, 0)
double upx, double upy, double upz,
//up vector :(0, 1, 0)
float m[16])
//View Matrix
{
double x[3], y[3], z[3], mag;
// Difference eye and center vectors to make Z vector.
z[0] = eyex - centerx;
z[1] = eyey - centery;
z[2] = eyez - centerz;
// Normalize Z.
mag = sqrt(z[0]*z[0] + z[1]*z[1] + z[2]*z[2]);
if (mag) {
z[0] /= mag;
z[1] /= mag;
z[2] /= mag;
}
// Up vector makes Y vector.
y[0] = upx;
y[1] = upy;
y[2] = upz;
// X vector = Y cross Z.
x[0] = y[1]*z[2] - y[2]*z[1];
x[1] = -y[0]*z[2] + y[2]*z[0];
x[2] = y[0]*z[1] - y[1]*z[0];
// Recompute Y = Z cross X.
y[0] = z[1]*x[2] - z[2]*x[1];
y[1] = -z[0]*x[2] + z[2]*x[0];
y[2] = z[0]*x[1] - z[1]*x[0];
// Normalize X.
mag = sqrt(x[0]*x[0] + x[1]*x[1] + x[2]*x[2]);
if (mag) {
x[0] /= mag;
x[1] /= mag;
x[2] /= mag;
}
// Normalize Y.
mag = sqrt(y[0]*y[0] + y[1]*y[1] + y[2]*y[2]);
if (mag) {
y[0] /= mag;
y[1] /= mag;
y[2] /= mag;
}
// Build resulting view matrix.
m[0*4+0] = x[0]; m[0*4+1] = x[1];
m[0*4+2] = x[2]; m[0*4+3] = -x[0]*eyex + -x[1]*eyey + -x[2]*eyez;
m[1*4+0] = y[0]; m[1*4+1] = y[1];
m[1*4+2] = y[2]; m[1*4+3] = -y[0]*eyex + -y[1]*eyey + -y[2]*eyez;
m[2*4+0] = z[0]; m[2*4+1] = z[1];
m[2*4+2] = z[2]; m[2*4+3] = -z[0]*eyex + -z[1]*eyey + -z[2]*eyez;
m[3*4+0] = 0.0; m[3*4+1] = 0.0; m[3*4+2] = 0.0; m[3*4+3] = 1.0;
}
申明:
部分文字选自: http://www.cnblogs.com/glshader/archive/2011/01/20/1940550.html
程序选自:NVIDIA Corporation\Cg\examples\OpenGL\basic\08_vertex_transform