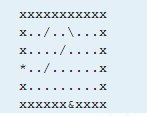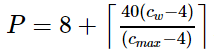The tables must be formatted precisely as outlined by the rules and examples provided. Mistakes that involve solely errant whitespace will be categorized as Presentation Error; all other errors will be reported as Wrong Answer.
#include<stdio.h>
const int N =100;
int main()
{
int A,B,C,a[N],b[N],c[N],lenA,lenB,lenC,flag;
while(scanf("%d%d",&A,&B)>0)
{
if(A==0&&B==0)
break;
C=A*B;
lenA=lenB=lenC=0;
while(A)
{
a[++lenA]=A%10; A/=10;
}
while(B)
{
b[++lenB]=B%10; B/=10;
}
while(C)
{
c[++lenC]=C%10; C/=10;
}
for(int i=1,j=lenA;i<j;i++,j--)
{
A=a[i];a[i]=a[j];a[j]=A;
}
flag=lenC;
printf("+-");
for(int i=1;i<=lenA;i++)
printf("----");
printf("--+\n");
printf("| ");
for(int i=1;i<=lenA;i++)
printf(" %d ",a[i]);
printf(" |\n");
for(int i=lenB;i>0;i--)
for(int j=1;j<=4;j++)
{
printf("|");
if(j!=2)
{
if(j!=4||lenC-lenA<i)
printf(" ");
else printf("%d",c[lenC--]);
}
else
{
if(flag-lenA>i)printf("/");
else printf(" ");
}
if(j==1)
{
printf("+");
for(int e=1;e<=lenA;e++)
printf("---+");
printf(" |\n");
}
else if(j==2)
{
for(int e=1;e<=lenA;e++)
printf("|%d /",(a[e]*b[i])/10);
printf("| |\n");
}
else if(j==3)
{
for(int e=1;e<=lenA;e++)
printf("| / ");
printf("|%d|\n",b[i]);
}
else
{
for(int e=1;e<=lenA;e++)
printf("|/ %d",(a[e]*b[i])%10);
printf("| |\n");
}
}
printf("| +");
for(int e=1;e<=lenA;e++)
printf("---+");
printf(" |\n");
printf("|");
if(flag>lenA)
printf("/");
else printf(" ");
while(lenC)
{
printf(" %d ",c[lenC--]);
if(lenC)
printf("/");
}
printf(" |\n");
printf("+-");
for(int i=1;i<=lenA;i++)
printf("----");
printf("--+\n");
}
}
/**************************************************************
Problem: 1561
User: aking2015
Language: C++
Result: Accepted
Time:0 ms
Memory:968 kb
****************************************************************/
American Carnival Makers Inc. (ACM) has a long history of designing rides and attractions. One of their more popular attractions is a fun house that includes a room of mirrors. Their trademark is to set up the room so that when looking forward from the entry door, the exit door appears to be directly ahead. However, the room has double-sided mirrors placed throughout at 45 degree angles. So, the exit door can be on any of the walls of the room. The set designer always places the entry and mirrors, but can never seem to be bothered to place the exit door. One of your jobs as part of the construction crew is to determine the placement of the exit door for the room given an original design.
The final diagram for a sample room is given below. The asterisk (*) marks the entry way, lower case x's mark the walls, the mirrors are given by the forward and backward slash characters (/ and \), open spaces with no visual obstructions are marked by periods (.), and the desired placement of the exit is marked with an ampersand (&). In the input diagram, there is an 'x' in place of the '&', since the exit has not yet been located. You need to alter the input diagram by replacing the proper 'x' with an '&' to identify the exit. Note that entrances and exits can appear on any of the walls (although never a corner), and that it is physically impossible for the exit to be the same as the entrance. (You don't need to understand why this is so, although it may be fun to think about.)
In both Java and C++ the backslash character (\) has special meaning as an escape character within character and string literals. You must use the combination \\ to express a single backslash within a character or string literal within source code.
DFS;模拟转向;注意下细节即可!
转载请注明出处: 寻找&星空の孩子
寻找&星空の孩子
题目链接:http://acm.csu.edu.cn/OnlineJudge/problem.php?id=1562
#include <iostream>
#include <stdio.h>
#include <string.h>
#include <stack>
#include <queue>
#include <map>
#include <set>
#include <vector>
#include <math.h>
#include <algorithm>
using namespace std;
#define ls 2*i
#define rs 2*i+1
#define up(i,x,y) for(i=x;i<=y;i++)
#define down(i,x,y) for(i=x;i>=y;i--)
#define mem(a,x) memset(a,x,sizeof(a))
#define w(a) while(a)
#define LL __int64
const double pi = acos(-1.0);
#define Len 100005
int n,m,cas = 1,sx,sy;
char str[25][25];
struct point
{
int x,y;
point() {}
point(int _x,int _y):x(_x),y(_y) {}
} ans;
point dfs(int x,int y,int d)
{
int tx = x,ty = y;
if(d==1) tx--;
if(d==2) tx++;
if(d==3) ty--;
if(d==4) ty++;
if(d==1)
{
w(1)
{
if(str[tx][ty]=='/') return dfs(tx,ty,4);
if(str[tx][ty]=='\\') return dfs(tx,ty,3);
if(tx==1 || str[tx][ty]=='x') return point(tx,ty);
tx--;
}
}
if(d==2)
{
while(1)
{
if(str[tx][ty]=='/') return dfs(tx,ty,3);
if(str[tx][ty]=='\\') return dfs(tx,ty,4);
if(tx==n || str[tx][ty]=='x') return point(tx,ty);
tx++;
}
}
if(d==3)
{
while(1)
{
if(str[tx][ty]=='/') return dfs(tx,ty,2);
if(str[tx][ty]=='\\') return dfs(tx,ty,1);
if(ty==1|| str[tx][ty]=='x') return point(tx,ty);
ty--;
}
}
if(d==4)
{
while(1)
{
if(str[tx][ty]=='/') return dfs(tx,ty,1);
if(str[tx][ty]=='\\') return dfs(tx,ty,2);
if(ty==m|| str[tx][ty]=='x') return point(tx,ty);
ty++;
}
}
}
int main()
{
int i,j;
w(~scanf("%d%d",&m,&n))
{
if(m+n==0)
break;
up(i,1,n)
{
scanf("%s",str[i]+1);
up(j,1,m)
{
if(str[i][j]=='*')
{
sx = i;
sy = j;
}
}
}
if(sx == 1) ans = dfs(sx,sy,2);
else if(sx == n) ans = dfs(sx,sy,1);
else if(sy == 1) ans = dfs(sx,sy,4);
else ans = dfs(sx,sy,3);
printf("HOUSE %d\n",cas++);
up(i,1,n)
{
up(j,1,m)
{
if(ans.x == i && ans.y == j)
{
printf("&");
continue;
}
printf("%c",str[i][j]);
}
puts("");
}
}
return 0;
}
/**************************************************************
Problem: 1562
User: aking2015
Language: C++
Result: Accepted
Time:0 ms
Memory:1484 kb
****************************************************************/
/*
10 10
xxxxxxxxxx
x.../\...x
x........x
x........x
x..//\..\x
*../\/../x
x........x
x........x
x...\/...x
xxxxxxxxxx
*/
Problem C: Lexicography
Time Limit: 1 Sec Memory Limit: 128 MB
Submit: 138 Solved: 42
[Submit][Status][Web Board]
Description
An anagram of a string is any string that can be formed using the same letters as the original. (We consider the original string an anagram of itself as well.) For example, the string ACM has the following 6 anagrams, as given in alphabetical order:
ACM
AMC
CAM
CMA
MAC
MCA
As another example, the string ICPC has the following 12 anagrams (in alphabetical order):
CCIP
CCPI
CICP
CIPC
CPCI
CPIC
ICCP
ICPC
IPCC
PCCI
PCIC
PICC
Given a string and a rank K, you are to determine the Kth such anagram according to alphabetical order.
Input
Each test case will be designated on a single line containing the original word followed by the desired rank K. Words will use uppercase letters (i.e., A through Z) and will have length at most 16. The value of K will be in the range from 1 to the number of distinct anagrams of the given word. A line of the form "# 0" designates the end of the input.
Output
For each test, display the Kth anagram of the original string.
Sample Input
ACM 5
ICPC 12
REGION 274
# 0
Sample Output
MAC
PICC
IGNORE
HINT
The value of K could be almost 245 in the largest tests, so you should use type long in Java, or type long long in C++ to store K.
用到了一个组合数学的结论:n个a,m个b,o个c,全排的个数为:(n+m+o)!/n!/m!/o! ;
对原先的字母排序,定首位依次往后全排;
转载请注明出处:寻找&星空の孩子
题目链接:http://acm.csu.edu.cn/OnlineJudge/problem.php?id=1563
#include <iostream>
#include <stdio.h>
#include <string.h>
#include <stack>
#include <queue>
#include <map>
#include <set>
#include <vector>
#include <math.h>
#include <algorithm>
using namespace std;
#define ls 2*i
#define rs 2*i+1
#define up(i,x,y) for(i=x;i<=y;i++)
#define down(i,x,y) for(i=x;i>=y;i--)
#define mem(a,x) memset(a,x,sizeof(a))
#define w(a) while(a)
#define LL long long
const double pi = acos(-1.0);
#define Len 100005
char str[50],ans[50];
LL f[50],m;
int main()
{
int i,j,k,len1,len2,cnt[50];
f[0] = 1;
up(i,1,16)
f[i]=f[i-1]*i;
w(~scanf("%s%lld",str,&m))
{
if(str[0]=='#'&&m==0)
break;
mem(cnt,0);
len1 = strlen(str);
sort(str,str+len1);
up(i,0,len1-1)
cnt[str[i]-'A']++;
up(i,0,len1-1)
{
LL last = 0,res;
up(j,0,25)
{
if(cnt[j])
{
res = f[len1-i-1];
up(k,0,25)
{
if(k==j) res/=f[cnt[k]-1];
else res/=f[cnt[k]];
}
if(last+res>=m)
{
ans[i] = j+'A';
m-=last;
cnt[j]--;
break;
}
else
last+=res;
}
}
}
ans[len1]='\0';
puts(ans);
}
return 0;
}
/**************************************************************
Problem: 1563
User: aking2015
Language: C++
Result: Accepted
Time:0 ms
Memory:1488 kb
****************************************************************/
Problem D: The Leprechaun Hunt
Time Limit: 10 Sec Memory Limit: 128 MB
Submit: 1 Solved: 1
[Submit][Status][Web Board]
Description
In Irish mythology, a Leprechaun is a small sprite who stores all his treasure in a hidden pot of gold at the end of the rainbow. If someone is able to catch the Leprechaun, he must give that person his pot of gold. In this problem, we explore the difficulty of capturing a Leprechaun.
We model a search with V villagers trying to catch a single Leprechaun as a game on a simple undirected graph having N ≥ 1+V nodes. To begin the game, the villagers position themselves at a subset of V distinct nodes. After that, the Leprechaun chooses a remaining node as a starting position. In each round of the game that follows, one villager moves from his or her current node to an adjacent node that is unoccupied by another villager. If that node has the Leprechaun, the villagers win the pot of gold. Otherwise, the Leprechaun now has the option of either staying at his current node, or moving to an adjacent, unoccupied node. Given a specific graph, and a fixed number of villagers, we are interested in the minimum number of turns the villagers need to capture the most clever of Leprechauns.
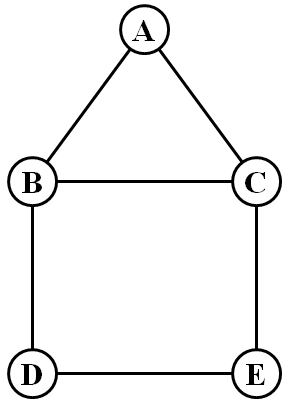
As examples, consider the two figures below. For the graph in Figure 1, a single villager can never capture a Leprechaun, as the Leprechaun can easily stay away from the villager. However, two villagers can capture the Leprechaun after at most 2 turns. For example, the villagers might begin at nodes A and D, in which case a clever Leprechaun will start at node F. But after the villager at A moves to G the villagers can capture the Leprechaun on their second turn, no matter whether the Leprechaun moves to E or remains at F.
For the graph in Figure 2, a single villager is unable to catch a clever Leprechaun. To see why this is the case, we describe a possible strategy of the Leprechaun, which is to always stay within the square made by BCDE, and opposite of the villager if the villager is in that square. If the villager were ever to go to A, the Leprechaun can remain still. In contrast, two villagers are able to capture the Leprechaun on their first move by picking initial positions such as B and E.
Figure 1:
Figure 2
Input
Each tests begins with a line containing three integers: V N E. The value of V denotes the number of villagers such that 1 ≤ V ≤ 7. The number of nodes N in the graph will satisfy 1 + V ≤ N ≤ 15. The value 1 ≤ E ≤ 45 designates the number of edges in the graph. Following the initial line of parameters will be one or more lines describing the edges of the graph, with up to 15 edges per line. Nodes of the graph are implicitly denoted with the first N uppercase letters (A, B, C, ...), and edges are explicitly denoted as two-character strings; for example the string AC denotes an edge connecting nodes A and C to each other. The E edges will be distinct, each edge connects two distinct nodes, and any node will have at most 6 incident edges. A line with the single value 0 designates the end of the input.
Output
For each test case, output a line, prefaced with the case number as shown in the example output below, followed by the minimum number of moves that the villagers need to guarantee capture of the Leprechaun, or the word NEVER if the villagers are unable to capture the Leprechaun.
Sample Input
1 7 7
AB BC CD DE EF FG GA
2 7 7
AB BC CD DE EF FG GA
1 5 6
AB AC BC BD DE EC
2 5 6
AB AC BC BD DE EC
2 10 15
AB BC CD DE EA AF BG CH DI EJ FH HJ JG GI IF
3 10 15
AB BC CD DE EA AF BG CH DI EJ FH HJ JG GI IF
3 14 10
AB BC CD EF FG GH IJ JK LM MN
4 14 10
AB BC CD EF FG GH IJ JK LM MN
0
Sample Output
CASE 1: NEVER
CASE 2: 2
CASE 3: NEVER
CASE 4: 1
CASE 5: NEVER
CASE 6: 1
CASE 7: NEVER
CASE 8: 2
HINT
暂,无解!
Problem E: Word Cloud
Time Limit: 1 Sec Memory Limit: 128 MB
Submit: 73 Solved: 37
[Submit][Status][Web Board]
Description
A word cloud (or tag cloud) is a visual representation of textual data based on a weighted metric. In the above cloud (which is based on this year's list of Mid-Central teams), the font size of each word is based on its number of occurrences in the data set. Tagg Johnson is a man obsessed with counting words that appear in online documents. On his computer, he keeps a spreadsheet of all the sites he visits, along with a list of words that appear on each site and the number of times such word appears. Tagg would like to generate word clouds based on the data he has collected.
Before describing the algorithm Tagg uses for generating clouds, we digress for a quick lesson in typography. The basic unit of measure is known as a point (typically abbreviated as pt). A font's size is described based on the vertical number of points from one line to the next, including any interline spacing. For example, with a 12pt font, the vertical space from the top of one character to the top of a character below it is 12 points. We assume that a character's height is precisely equal to the font's point size (regardless of whether the character is upper or lower case).
For this problem, we focus on a fixed-width font, such as Courier, in which each character of the alphabet is also given the same amount of width. The character width for such a font depends on the font size and the aspect ratio. For Courier, a word with t characters rendered in a font of size P has a total width of when measured in points. Note well the use of the ceiling operator, which converts any noninteger to the next highest integer. For example, a 5-letter word in a 20pt font would be rendered with a height of 20 points and a width equal to points.
Now we can describe Tagg's algorithm for creating a word cloud. He pre-sorts his word list into alphabetical order and removes words that do not occur at least five times. For each word w, he computes a point size based on the formula 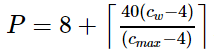 , where cw is the number of occurrences of the word, and cmax is the number of occurrences of the most frequent word in the data set. Note that by this formula, every word will be rendered with anywhere from a 9pt font to a 48pt font. He then places the words in rows, with a 10pt horizontal space between adjacent words, placing as many words as fit in the row, subject to a maximum width W for his entire cloud. The height of a given row is equal to the maximum font size of any word rendered in that row.
, where cw is the number of occurrences of the word, and cmax is the number of occurrences of the most frequent word in the data set. Note that by this formula, every word will be rendered with anywhere from a 9pt font to a 48pt font. He then places the words in rows, with a 10pt horizontal space between adjacent words, placing as many words as fit in the row, subject to a maximum width W for his entire cloud. The height of a given row is equal to the maximum font size of any word rendered in that row.
As a tangible example, consider the following data set and word cloud.
Word Count
apple 10
banana 5
grape 20
kiwi 18
orange 12
strawberry 10


In this example, apple is rendered with 23pt font using width 65pt, banana is rendered with 11pt font using width 38pt, and grape is rendered with 48pt font and width 135pt. If the overall word cloud is constrained to have width at most 260, those three words fit in a row and the overall height of that row is 48pt (due to grape). On the second row kiwi is rendered with height 43pt and width 97pt, and orange is rendered with height 28pt and width 95pt. A third row has strawberry with height 23pt and width 130pt. The overall height of this word cloud is 114pt.
Input
Each data set begins with a line containing two integers: W and N. The value W denotes the maximum width of the cloud; W ≤ 5000 will be at least as wide as any word at its desired font size. The value 1 ≤ N ≤ 100 denotes the number of words that appear in the cloud. Following the first line are N additional lines, each having a string S that is the word (with no whitespace), and an integer C that is a count of the number of occurrences of that word in the original data set, with 5 ≤ C ≤ 1000. Words will be given in the same order that they are to be displayed within the cloud.
Output
For each data set, output the word CLOUD followed by a space, a serial number indicating the data set, a colon, another space, and the integer height of the cloud, measured in font points.
Sample Input
260 6
apple 10
banana 5
grape 20
kiwi 18
orange 12
strawberry 10
250 6
apple 10
banana 5
grape 20
kiwi 18
orange 12
strawberry 10
610 6
apple 10
banana 5
grape 20
kiwi 18
orange 12
strawberry 10
0 0
Sample Output
CLOUD 1: 114
CLOUD 2: 99
CLOUD 3: 48
HINT
给你宽度W,用题目中的公式求没个单词的高度(P)和宽度w,问最后总高度,注意:是按顺序排的,刚刚开始我没注意,以为要dp,如果按顺序那么只要判断有没有越界就可以了,越界就放下一行。这里注意下两个单词之间有10个单位的距离。然后Cw 表示count;Cmax 表示max(count);
转载请注明出处:寻找&星空の孩子
题目链接:http://acm.csu.edu.cn/OnlineJudge/problem.php?id=1565
#include <iostream>
#include <stdio.h>
#include <string.h>
#include <stack>
#include <queue>
#include <map>
#include <set>
#include <vector>
#include <math.h>
#include <algorithm>
using namespace std;
#define ls 2*i
#define rs 2*i+1
#define up(i,x,y) for(i=x;i<=y;i++)
#define down(i,x,y) for(i=x;i>=y;i--)
#define mem(a,x) memset(a,x,sizeof(a))
#define w(a) while(a)
#define LL long long
const double pi = acos(-1.0);
#define Len 100005
int w,n;
char str[105][1005];
int s[105],P[105],W[105],len[105],maxn;
int main()
{
int i,j,k,cas = 1,ans;
w(~scanf("%d%d",&w,&n))
{
if(w+n==0)
break;
maxn = 0;
up(i,0,n-1)
{
scanf("%s%d",str[i],&s[i]);
len[i] = strlen(str[i]);
maxn = max(maxn,s[i]);
}
up(i,0,n-1)
{
P[i] = 8+(int)ceil(1.0*40*(s[i]-4)/(maxn-4));
W[i] = (int)ceil(1.0*9*len[i]*P[i]/16);
}
ans = 0;
int flag = 1,maxH=0,now;
up(i,0,n-1)
{
if(flag)
{
ans+=maxH;
maxH=0;
flag=0;
maxH=max(maxH,P[i]);
now=W[i];
}
else
{
if(now+10+W[i]<=w)
{
now+=10+W[i];
maxH=max(maxH,P[i]);
}
else
{
flag=1;
i--;
}
}
}
printf("CLOUD %d: %d\n",cas++,ans+maxH);
}
return 0;
}
/**************************************************************
Problem: 1565
User: aking2015
Language: C++
Result: Accepted
Time:0 ms
Memory:1588 kb
****************************************************************/
Problem F: The Maze Makers
Time Limit: 1 Sec Memory Limit: 128 MB
Submit: 66 Solved: 21
[Submit][Status][Web Board]
Description
The Maze Makers is a publisher of puzzle books. One of their most popular series is maze books. They have a program that generates rectangular two-dimensional mazes like the one shown in Figure 1. The rules for these mazes are: (1) A maze has exactly two exterior cell walls missing, opening to two distinct terminal cells, (2) starting from any one cell, all other cells are reachable, (3) between any two cells in the maze there is exactly one simple path. Formally, a path is a sequence of cells where each cell and its successor on the path share an edge without a wall. A simple path is a path that never repeats a cell.
The Maze Maker program uses hexadecimal digits to encode the walls and passages of a maze. For each cell in the maze there is a corresponding hex digit. As shown in Figure 2, the 1's and 0's in the 4 digit binary representation of a hex digit correspond to the walls (1's) and passages (0's) for each cell in the maze. For example, the binary encoding for the hex digit B is 1011. Starting at the top of the cell and moving clockwise around it, this digit represents a cell with a wall at the top, a passage to the right and walls at the bottom and to the left. A path between two maze cells successively moves one cell up, down, left or right, going through passages only.
Figure 1: Sample Maze
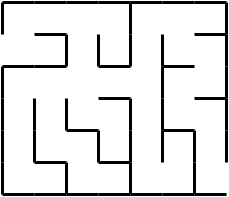
Figure 2: Hex Code for Walls and Passageways
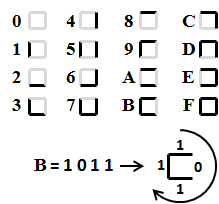
Figure 3: Maze with Cell Labels
Figure 3 shows the sample maze with the hexadecimal labels in each cell. For example, the hexadecimal digit E in the top-right cell indicates that it has a wall above it, to its right, below it, yet a passageway to its left. The hexadecimal digit 8 to its left indicates that its cell has only a wall above it. The inputs will always be self-consistent, in that the hexadecimal digits in neighboring cells will agree on whether they share a wall or passageway, and each input will always have precisely two terminal cells, each with one missing exterior wall.
Our sample maze is a legitimate maze in that all cells are reachable and there is a unique simple path between any pairs of cells in the maze. Your goal is to write a program that reads the hexadecimal descriptions of a potential maze and tests to determine if it is legitimate. If there is a problem, your program must report only the first problem, as detailed below in the section titled "Output".
Input
The input consists of the descriptions of one or more candidate mazes. Each maze description will start with two integers, H and W, indicating the height and width of the maze, respectively, such that 1 ≤ H ≤ 50 and 2 ≤ W ≤ 50. Following this first line will be H rows of hexadecimal digits, with each row consisting of W digits. The input is terminated with a line displaying a pair of zeros.
Output
For each candidate maze, the program should output the first one of the following statements that applies:
NO SOLUTION
UNREACHABLE CELL
MULTIPLE PATHS
MAZE OK
The classification statements are defined formally as follows:
NO SOLUTION - There is no path through the interior of the maze between the two exterior openings.
UNREACHABLE CELL - There is at least one cell in the maze that is not reachable by following passageways from either of the openings in the exterior walls of the maze.
MULTIPLE PATHS - There exists a pair of cells in the maze that have more than one simple path between them. Two simple paths are considered to be distinct if any part of the paths differ.
MAZE OK - None of the above problems exist.
Note well that for the second case given in the following examples, there is no path between the start and finish and there is an unreachable cell; the correct output should simply be NO SOLUTION, because that error message is listed first in the above list. Similarly, in the fourth example given, UNREACHABLE CELL is reported because that error has priority over the multiple paths.
Sample Input
6 7
9A8C98E
2E5753C
980A496
553C53C
53C75D5
3E3E363
3 3
F9A
D3E
3AC
1 8
3AAA8AAE
6 3
9AC
3C5
A24
9A6
5BC
3C7
5 4
8A8E
592C
5186
161C
3A63
5 4
8AAE
59AC
5386
1E1C
3A63
0 0
Sample Output
MAZE OK
NO SOLUTION
MAZE OK
UNREACHABLE CELL
MULTIPLE PATHS
MULTIPLE PATHS
HINT
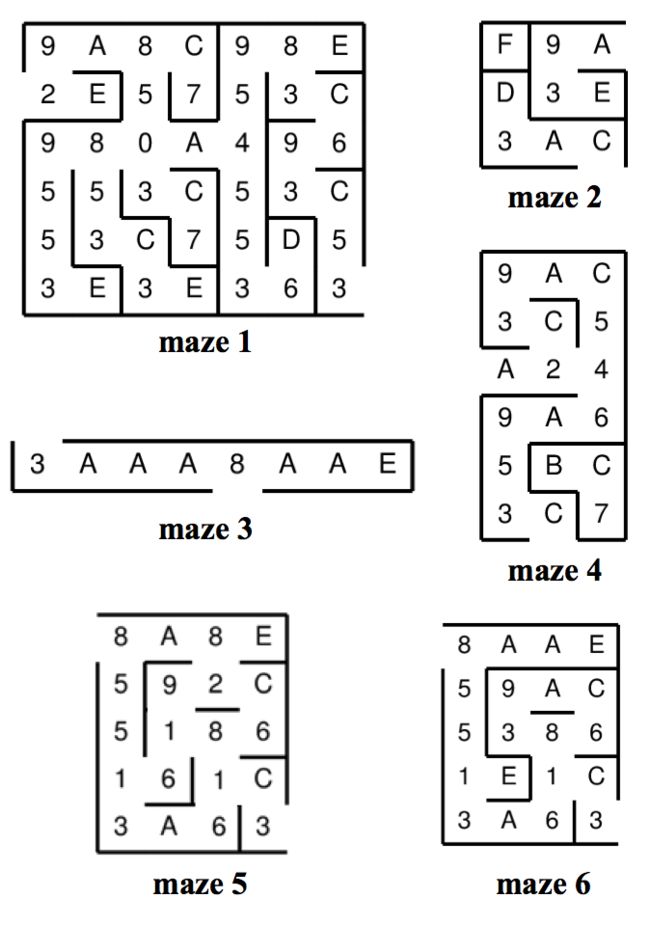
注意:结果的优先级,模拟+二进制
转载请注明出处:寻找&星空の孩子
题目链接:http://acm.csu.edu.cn/OnlineJudge/problem.php?id=1566
#include <iostream>
#include <stdio.h>
#include <string.h>
#include <stack>
#include <queue>
#include <map>
#include <set>
#include <vector>
#include <math.h>
#include <algorithm>
using namespace std;
#define ls 2*i
#define rs 2*i+1
#define up(i,x,y) for(i=x;i<=y;i++)
#define down(i,x,y) for(i=x;i>=y;i--)
#define mem(a,x) memset(a,x,sizeof(a))
#define w(a) while(a)
#define LL long long
const double pi = acos(-1.0);
#define Len 100005
int n,m;
int maze[65][65],sx,sy,ex,ey,flag;
char str[1000];
int to[4][3] = {1,0,2,-1,0,8,0,1,4,0,-1,1},vis[65][65];
struct node
{
int x,y;
};
int main()
{
int i,j,k;
while(~scanf("%d%d",&n,&m))
{
if(!n&&!m) break;
mem(vis,0);
up(i,1,n)
{
scanf("%s",str+1);
up(j,1,m)
{
vis[i][j];
if(str[j]>='0'&&str[j]<='9') maze[i][j] = str[j]-'0';
else maze[i][j]=str[j]-'A'+10;
maze[i][j]=~maze[i][j];
}
}
sx = 0;
up(i,1,n)
{
if(maze[i][1]&1)
{
if(!sx) sx=i,sy=1;
else ex=i,ey=1;
}
if(maze[i][m]&4)
{
if(!sx) sx=i,sy=m;
else ex=i,ey=m;
}
}
up(i,1,m)
{
if(maze[1][i]&8)
{
if(!sx) sx=1,sy=i;
else ex=1,ey=i;
}
if(maze[n][i]&2)
{
if(!sx) sx=n,sy=i;
else ex=n,ey=i;
}
}
int mul=0;
queue<node> Q;
node a,next;
a.x = sx;
a.y = sy;
Q.push(a);
vis[sx][sy] = 16;
while(!Q.empty())
{
a = Q.front();
Q.pop();
up(i,0,3)
{
if(vis[a.x][a.y]==to[i][2])continue;
if(maze[a.x][a.y]&to[i][2])
{
next.x = a.x+to[i][0];
next.y = a.y+to[i][1];
if(next.x>=1 && next.x<=n && next.y>=1 && next.y<=m)
{
if(vis[next.x][next.y]) mul=1;
else
{
if(to[i][2]==1) vis[next.x][next.y] = 4;
else if(to[i][2]==4) vis[next.x][next.y] = 1;
else if(to[i][2]==2) vis[next.x][next.y] = 8;
else if(to[i][2]==8) vis[next.x][next.y] = 2;
Q.push(next);
// printf("%d %d %d\n",next.x,next.y,vis[next.x][next.y]);
}
}
}
}
}
// printf("[%d %d %d]\n",ex,ey,vis[ex][ey]);
if(vis[ex][ey])
{
flag = 0;
up(i,1,n)
{
up(j,1,m)
{
if(!vis[i][j])
{
flag = 1;
break;
}
}
if(flag)
break;
}
if(flag)
printf("UNREACHABLE CELL\n");
else
{
if(mul) printf("MULTIPLE PATHS\n");
else printf("MAZE OK\n");
}
}
else
printf("NO SOLUTION\n");
}
return 0;
}
/**************************************************************
Problem: 1566
User: aking2015
Language: C++
Result: Accepted
Time:12 ms
Memory:1528 kb
****************************************************************/
Problem G: Reverse Rot
Time Limit: 1 Sec Memory Limit: 128 MB
Submit: 148 Solved: 81
[Submit][Status][Web Board]
Description
A very simplistic scheme, which was used at one time to encode information, is to rotate the characters within an alphabet and rewrite them. ROT13 is the variant in which the characters A-Z are rotated 13 places, and it was a commonly used insecure scheme that attempted to "hide" data in many applications from the late 1990's and into the early 2000's.
It has been decided by Insecure Inc. to develop a product that "improves" upon this scheme by first reversing the entire string and then rotating it. As an example, if we apply this scheme to string ABCD with a reversal and rotation of 1, after the reversal we would have DCBA and then after rotating that by 1 position we have the result EDCB.
Your task is to implement this encoding scheme for strings that contain only capital letters, underscores, and periods. Rotations are to be performed using the alphabet order:
ABCDEFGHIJKLMNOPQRSTUVWXYZ_.
Note that underscore follows Z, and the period follows the underscore. Thus a forward rotation of 1 means 'A' is shifted to 'B', that is, 'A'→'B', 'B'→'C', ..., 'Z'→'_', '_'→'.', and '.'→'A'. Likewise a rotation of 3 means 'A'→'D', 'B'→'E', ..., '.'→'C'.
Input
Each input line will consist of an integer N, followed by a string. N is the amount of forward rotation, such that 1 ≤ N ≤ 27. The string is the message to be encrypted, and will consist of 1 to 40 characters, using only capital letters, underscores, and periods. The end of the input will be denoted by a final line with only the number 0.
Output
For each test case, display the "encrypted" message that results after being reversed and then shifted.
Sample Input
1 ABCD
3 YO_THERE.
1 .DOT
14 ROAD
9 SHIFTING_AND_ROTATING_IS_NOT_ENCRYPTING
2 STRING_TO_BE_CONVERTED
1 SNQZDRQDUDQ
0
Sample Output
EDCB
CHUHKWBR.
UPEA
ROAD
PWRAYF_LWNHAXWH.RHPWRAJAX_HMWJHPWRAORQ.
FGVTGXPQEAGDAQVAIPKTVU
REVERSE_ROT
HINT
转载请注明出处:寻找&星空の孩子
题目链接:http://acm.csu.edu.cn/OnlineJudge/problem.php?id=1567
#include<stdio.h>
#include<string.h>
int main()
{
char str[45],mod[]={"ABCDEFGHIJKLMNOPQRSTUVWXYZ_."},ch;
int n;
while(scanf("%d",&n)>0&&n)
{
//getchar();
scanf("%s",str);
int len=strlen(str);
for(int i=0,j=len-1;i<j;i++,j--)
{
ch=str[i]; str[i]=str[j];str[j]=ch;
}
for(int i=0;i<len;i++)
{
for(int j=0;j<28;j++)
if(str[i]==mod[j])
{
if(j+n<28)
printf("%c",mod[j+n]);
else
printf("%c",mod[j+n-28]);
}
}
printf("\n");
}
}
Problem H: Shrine Maintenance
Time Limit: 2 Sec Memory Limit: 128 MB Special Judge
Submit: 64 Solved: 27
[Submit][Status][Web Board]
Description
A religious sect has holy sites with shrines placed around a circle of radius 1000. The circle is split into N equal length arcs and the endpoints are numbered in order, 1 through N. The first figure shows a circle where N is 12, with 12 gray tick marks like on a 12-hour analog clock. We can imagine the marks numbered, as on a clock, with 12 at the top. Each circle has one or more sacred numbers associated with it. The sacred numbers for the circle in the first figure are 2 and 3. A shrine, indicated by a black dot in the figure, is placed at each mark whose number is a multiple of at least one of the sacred numbers, so in this case the shrines are at positions 2, 3, 4, 6, 8, 9, 10, and 12.

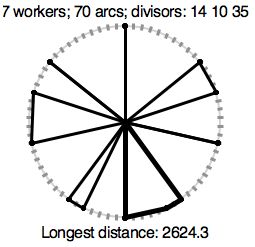
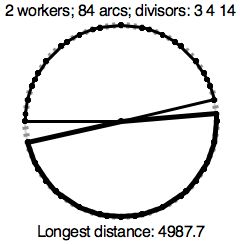
When it comes time to inspect and repair the shrines at a given site, the area is closed and a team of workers simultaneously fan out from a maintenance shed, located in the center of the circle, so that each shrine is visited by at least one worker. Once all workers have returned to the shed, the site is reopened to the public. Because these sites are in great demand, it is important that they be closed as briefly as possible. In order to minimize this time, they must figure out how to apportion the shrines among the current number of workers, so the maximum distance traveled by any one worker is as small as possible. Figure 1 shows one choice for the optimal solution paths for 3 workers. The lower left path has darker lines, to indicate that it is one with the longest length, which in this case is approximately 3517.6.
This sect has many circular sites with multiple shrines. The number of available workers at a site, W, the value of the number equal arcs, N, and the sacred numbers vary between sites. The sacred numbers are always divisors of N. Your job is to help figure out how much time is required for maintenance. Figures 2 and 3 show optimal solutions for other sites.
Input
The input consists of one or more data sets. Each data set is on a single line and consists entirely of positive integers. The first three entries are W, the number of workers, N, the number of equal arcs around the circle, and D, the number of sacred divisors of N. At the end come the D divisors of N. W is no more than the total number of shrines; N ≤ 8600, and D ≤ 6; each listed divisor of N is smaller than N.
A single zero, 0, will be placed on the last line to indicate the end of the input.
Output
The output is a single line for each dataset: the maximum distance a worker must travel with an optimal assignment of the shrines. This number is displayed so that it is rounded to one decimal place, and always shows that decimal place, even if it is 0. To ensure unique answers with double arithmetic, the datasets are chosen so that if your answer is anywhere within .005 of the exact minimum distance, then the answer rounded to one decimal place will be the same.
The first three sample datasets correspond to the three figures.
Caution: Be careful with your algorithm so it finishes rapidly.
Sample Input
3 12 2 2 3
7 70 3 14 10 35
2 84 3 3 4 14
4 35 2 7 5
3 20 2 5 4
3 6 1 1
4 6 1 1
1 6 1 1
8600 8600 3 1 10 100
0
Sample Output
3517.6
2624.3
4987.7
3224.9
3488.4
3000.0
3000.0
7000.0
2000.0
HINT
没看题!
Problem I: Wet Tiles
Time Limit: 60 Sec Memory Limit: 512 MB
Submit: 73 Solved: 34
[Submit][Status][Web Board]
Description
Alice owns a construction company in the town of Norainia, famous for its unusually dry weather. In fact, it only rains a few days per year there. Because of this phenomenon, many residents of Norainia neglect to do roof repairs until leaks occur and ruin their floors. Every year, Alice receives a deluge of calls from residents who need the leaks fixed and floor tiles replaced. While exquisite in appearance, Norainia floor tiles are not very water resistant; once a tile becomes wet, it is ruined and must be replaced. This year, Alice plans to handle the rainy days more efficiently than in past years. She will hire extra contractors to dispatch as soon as the calls come in, so hopefully all leaks can be repaired as soon as possible. For each house call, Alice needs a program to help her determine how many replacement tiles a contractor team will need to bring to complete the job.
For a given house, square floor tiles are arranged in a rectangular grid. Leaks originate from one or more known source locations above specific floor tiles. After the first minute, the tiles immediately below the leaks are ruined. After the second minute, water will have spread to any tile that shares an edge with a previously wet tile. This pattern of spreading water continues for each additional minute. However, the walls of a house restrict the water; if a damaged area hits a wall, the water does not penetrate the wall. We assume there are always four outer walls surrounding the entire house. A house may also have a number of additional "inner" walls; each inner wall is comprised of a connected linear sequence of locations (which may or may not be connected to the outer walls or to each other).
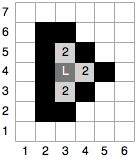
As an example, Figure 1 shows water damage (in gray) that would result from three initial leaks (each marked with a white letter 'L') after each of the first five minutes of time. Tiles labeled '2' become wet during the second minute, tiles labeled '3' become wet during the third minute, and so forth. The black areas designate inner walls that restrict the flow of water. Note that after 5 minutes, a total of 75 tiles have been damaged and will need to be replaced. Figures 2 through 4 show other houses that correspond to the example inputs for this problem.
75 wet tiles
17 wet tiles
4 wet tiles
94 wet tiles
Input
Each house is described beginning with a line having five integral parameters: X Y T L W. Parameters X and Y designate the dimensions of the rectangular grid, with 1 ≤ X ≤ 1000 and 1 ≤ Y ≤ 1000. The coordinate system is one-indexed, as shown in the earlier figures. Parameter T designates the number of minutes that pass before a team of contractors arrives at a house and stops the leaks, with 1 ≤ T ≤ 200000. The parameter L designates the number of leaks, with 1 ≤ L ≤ 100. Parameter W designates the number of inner walls in the house, 0 ≤ W ≤ 100.
The following 2L integers in the data set, on one or more lines, are distinct (x y) pairs that designate the locations of the L distinct leaks, such that 1 ≤ x ≤ X and 1 ≤ y ≤ Y.
If W > 0, there will be 4W additional integers, on one or more lines, that describe the locations of the walls. For each such wall the four parameters (x1,y1), (x2,y2) describe the locations of two ends of the wall. Each wall replaces a linear sequence of adjoining tiles and is either axis-aligned or intersects both axes at a 45 degree angle. Diagonal walls are modeled as a sequence of cells that would just be touching corner to corner. If the two endpoints of a wall are the same, the wall just occupies the single cell at that location. Walls may intersect with each other, but no leak is over a wall.
There will be one or more houses in the data file and a line with a single integer -1 designates the end of the data set.
Output
For each house, display the total number of tiles that are wet after T minutes.
Sample Input
12 12 5 3 5
2 11 3 3 9 5
1 9 6 9 1 7 4 4 7 1 7 4
10 9 10 12 11 4 12 4
9 7 8 1 3
4 3
2 2 6 6 6 2 2 6 8 2 8 2
6 7 50 1 3
3 4
2 2 2 6 3 6 5 4 5 4 3 2
12 12 5 3 0
2 11 3 3 9 5
-1
Sample Output
75
17
4
94
HINT
BFS
转载请注明出处:寻找&星空の孩子
题目链接:http://acm.csu.edu.cn/OnlineJudge/problem.php?id=1569
#include<stdio.h>
#include<string.h>
#include<queue>
using namespace std;
const int N = 1005;
struct locate
{
int x,y;
};
int mapt[N][N],n,m,T,dir[4][2]={0,1,0,-1,1,0,-1,0};
queue<locate>q[2];
void bfs(int flag)
{
locate pre,now;
while(!q[flag].empty())
{
pre=q[flag].front();q[flag].pop();
for(int e=0;e<4;e++)
{
now.x=pre.x+dir[e][0];
now.y=pre.y+dir[e][1];
if(now.x>0&&now.x<=n&&now.y>0&&now.y<=m&&mapt[now.x][now.y]==0)
{
mapt[now.x][now.y]=1;
q[!flag].push(now);
}
}
}
}
int main()
{
int L,W;
locate now,pre;
while(scanf("%d",&n)>0&&n!=-1)
{
scanf("%d%d%d%d",&m,&T,&L,&W);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
mapt[i][j]=0;
while(!q[0].empty())q[0].pop();
while(!q[1].empty())q[1].pop();
while(L--)
{
scanf("%d%d",&now.x,&now.y); q[0].push(now);mapt[now.x][now.y]=1;
}
while(W--)
{
scanf("%d%d%d%d",&pre.x,&pre.y,&now.x,&now.y);
if(now.x>pre.x)
{
int tt;
tt=pre.x; pre.x=now.x; now.x=tt;
tt=pre.y; pre.y=now.y; now.y=tt;
}
if(pre.x==now.x)
{
if(pre.y<now.y)
{
int tt=pre.y; pre.y=now.y; now.y=tt;
}
while(pre.y>=now.y)
{
mapt[pre.x][pre.y--]=2;
}
}
else if(pre.y==now.y)
{
if(pre.x<now.x)
{
int tt=pre.x; pre.x=now.x; now.x=tt;
}
while(pre.x>=now.x)
{
mapt[pre.x--][pre.y]=2;
}
}
else if(pre.x>=now.x&&pre.y<=now.y)
{
while(now.x<=pre.x&&now.y>=pre.y)
{
mapt[now.x][now.y]=2;
now.y--; now.x++;
}
}
else
{
while(now.x<=pre.x&&now.y<=pre.y)
{
mapt[pre.x][pre.y]=2;
pre.y--; pre.x--;
}
}
}
int flag=0;
while(!q[flag].empty())
{T--;
if(T==0) break;
bfs(flag); flag=!flag;
}
int ans=0;
for(int j=m;j>=1;j--)
{
for(int i=1;i<=n;i++)
{
//printf("%d ",mapt[i][j]);
if(mapt[i][j]==1)
ans++;
}
//printf("\n");
}
printf("%d\n",ans);
}
}
/**************************************************************
Problem: 1569
User: aking2015
Language: C++
Result: Accepted
Time:1068 ms
Memory:5012 kb
****************************************************************/