Stanford ML - 机器学习应用

前面讲了线性回归，逻辑回归和神经网络，一个个的知识点，这周的课程主要讲一些应用机器学习的方法和注意事项，这样就把前面的点融合到解决现实问题中来了。对于一个机器学习算法，如何评价它的好坏呢？可以把数据分成训练集和测试集，根据训练集得到参数Theta，然后在测试集上计算误差，通过误差的大小衡量算法的性能。那些因素可以影响算法呢？这里包括训练集的大小，特征的多少（overfit，underfit)，正则参数lambda的大小等。机器学习算法可以通过调整特征数量和正则参数来优化性能。

假设这里是多项式线性回归，那么特征数量体现在维度上。如何选择维度呢？可以依次尝试，从一维到N维，在训练集上拟合参数Theta，然后在测试集上计算误差；选择误差最小的维度作为算法的维度。这种方式因为维度是根据测试集选择的，往往会乐观估计实际的误差。所以呢，进一步把数据划分为训练集（60%），验证集（20%）和测试集（20%），根据验证集选择维度，在测试集上评估误差。这样误差估算就比较准确了。

算法分析是很重要的，当算法性能不好时，它可以告诉你往哪个方向努力。首先我们要区分出算法是High bias (underfit)还是High variance (overfit)。通过在训练集和验证集上分别计算误差，可以很容易的判断是High bias 还是High variance，如下。

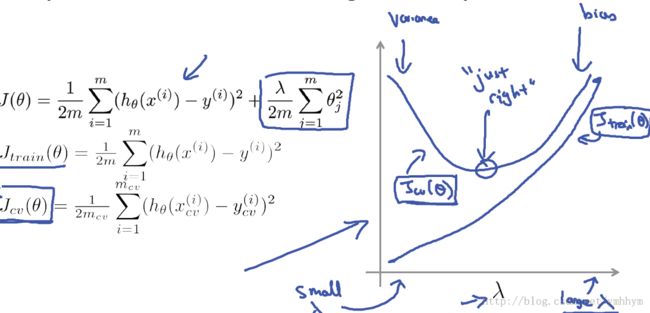
加入正则项之后，怎么选择正则参数lambda呢？跟选择维度类似，我们从0开始，在训练集上拟合lambda为0, 0.01, 0.02, 0.04, 0.08, 0.16, ..., 10时的Theta，然后在验证集上计算误差，选择误差最小时的lambda。这里呢，只是拟合的时候引入正则项，评估误差的时候正则项不计入。对应不同的lambda，可以绘制出相应训练集和验证集上的误差如下，可以看出这影响算法是High bias 还是High variance。最优lambda的取值对应验证集误差的最低点。

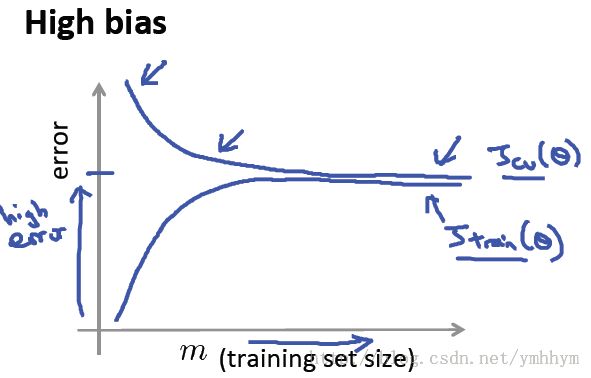
通过绘制学习曲线（不同训练集大小时的误差），可以很容易的判断增加训练集数据能否提高算法性能 - 最终也是归结到High bias 还是High variance问题。可以看出只有在算法经受high variance问题时，增加训练集数据才管用。

这样如果要解决high bias问题，我们可以提取更多特征，增加多项式特征，减小lambda。对应的如果要解决high variance问题，我们可以考虑收集更多训练数据，减少特征数量，增加lambda。

具体应用机器学习解决实际问题时，我们应该快速开发一个简单的算法，通过上面的学习曲线分析往哪个方向努力。对误差进行分析，往往都可以找到一些提高算法的规律；定量化则是一个重要的手段，一切靠数据来说话。

有时候呢，单一的准确率(accuracy rate)并不能很好的反应算法的性能，比如对skewed classes。这里引入了Precision rate和Recall rate来综合衡量 - 信息检索里面的经典概念 - F1 Score = 2(P*R)/(P+R)。当特征包含足够多的信息，并且算法有很多参数的时候（low bias)，增加训练集（low variance）会提高算法的性能。