树状数组（Fenwick tree，又名binary indexed tree

  

树状数组（Fenwick tree，又名binary indexed tree），是一种很实用的数据结构。它通过用节点i，记录数组下标在[ i –2^k + 1, i]这段区间的所有数的信息（其中，k为i的二进制表示中末尾0的个数，设lowbit(i) = 2^k），实现在O(lg n) 时间内对数组数据的查找和更新。

树状数组的传统解释图，不能很直观的看出其所能进行的更新和查询操作。其最主要的操作函数lowbit(k)与数的二进制表示相关，本质上仍是一种二分。因而可以通过二叉树，对其进行分析。事实上，从二叉树图，我们对它所能进行的操作和不能进行的操作一目了然。

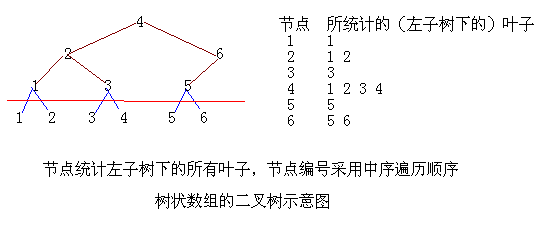
和前面提到的点树类似，先画一棵二叉树，然后对节点中序遍历（点树是采用广度优先），每个节点仍然只记录左子树信息，见图：

 

 

 

由于采用的是中序遍历，从节点1到节点k时，刚好有k个叶子被统计。

可以证明：

  叶子k，一定在节点k的左子树下。

  以节点k为根的树，其左子树共有叶子lowbit(k)

节点k的父节点是：k + lowbit(k) 或 k - lowbit(k) 

节点k + lowbit(k) 是节点k的最近父节点，且节点k在它的左子树下。

节点k - lowbit(k) 是节点k的最近父节点，且节点k在它的右子树下。

节点k，统计的叶子范围为：(k - lowbit(k),  k]。

节点k的左孩子是：k - lowbit(k) / 2

 

下面分析树状数组两面主要应用：

1 更新数据x，进行区间查询。

2 更新区间，查询某个数。

由于，树状数组只统计了左子树的信息，因而只能查询更新区间[1, x]。只在在满足[x,y]的信息可以由[1,x-1]和[1,y]的信息推导出时，才能进行区间[x,y]的查询更新。这也是树状数组不能用于任意区间求最值的根本原因。

 

先定义两个集合：

up_right(k) ：节点k所有的父节点，且节点k在它们的左子树下。

up_left(k) ：  节点k所有的父节点，且节点k在它们的右子树下。

 

1  更新数据x，查询区间[1,y]。

显然，更新叶子x，要找出叶子x在哪些节点的左子树下。因而节点k、所有的up_right(k)

都要更新。

查询[1, y]，实际上就是把该区间拆分成一系列小区间，并找出统计这些区间的节点。可以通过找出y在哪些节点的右子树下，这些节点恰好不重复的统计了区间[1, y-1]。因而要访问节点y、所有的up_left(y)。

 

2 更新区间[1,y]，查询数据x

  这和前面的操作恰好相反。与前面的最大不同之处在于：节点保存的不再是其叶子总个数这些信息，而是该区间的所有叶子都改变了多少。也就是说：每个叶子的信息，分散到了所有对它统计的节点上。因此操作和前面相似：

  更新[1,y]时，更新节点y、所有up_left(y)。

  查询x时，  访问x、所有up_right(x)。

 

前面的树状数组，只对左子树信息进行统计，如果从后往前读数据初始化树状数组，则变成只对右子树信息进行统计，这时更新和查询操作，刚好和前面的相反。

 

一般情况下，树状数组比点树省空间，对区间[1, M]只要M+1空间，查询更新时定位节点比较快，定位父节点和左右孩子相对麻烦点（不过，一般也不用到。从上往下查找，可参考下面代码中的erease_nth函数（删除第n小的数））。

 

下面是使用树状数组的实现代码（求逆序数和模拟约瑟夫环问题）：