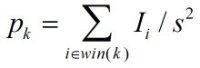超分辨率成像模型中下采样矩阵的构造

转自：http://blog.sina.com.cn/s/blog_672c5a470100pmj6.html

代码：

function A = create_DS(HR,s)
% produce the down-scaling matrix A
[m,n] = size(HR); % the colume and row of HR image
As = (1/s^2).*ones(1,s);
BA = DiagonalCat(m/s,As);
CA = repmat(BA,1,s);
A = DiagonalCat(n/s,CA);


function [out] = DiagonalCat(s,A)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%   produce block diagonal matrix
%   Copyright vvcumt(Liang Weiwei), DUT.  2010-09-27
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% % A =  
% %      1     1
% % s =
% %      3
% % out =
% %      1     1     0     0     0     0
% %      0     0     1     1     0     0
% %      0     0     0     0     1     1
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
[m,n] = size(A);% A is basic block
out = zeros(s*m,s*n);
for i = 1:s
    out((i-1)*m+1:i*m , (i-1)*n+1:i*n) = A;
end

原理：

对于一幅图像I尺寸为M*N，对其进行s倍下采样，即得到(M/s)*(N/s)尺寸的得分辨率图像，当然s应该是M和N的公约数才行，如果考虑的是矩阵形式的图像，就是把原始图像s*s窗口内的图像变成一个像素，这个像素点的值就是窗口内所有像素的均值：

那么如果图像按列向量化，变成了1*(MN)的向量之后，这个下采样过程也应当有一个对应的矩阵，这个矩阵的大小为(MN/s^2)*(MN)。

先以一个4*4的图像为例：数字代表像素位置

0   4   8   12

1   5   9   13

2   6   10  14

3   7   11  15

向量化的图像大小为16*1，元素为：

【0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15】

2倍下采样之后的新图像具有四个像素，分别是0 1 4 5位置的均值，2 3 6 7位置的均值，8 9 12 13位置的均值，10 11 14 15位置的均值。

这个下采样矩阵为：

0.25 0.25 0    0    0.25 0.25 0    0  ……

0    0    0.25 0.25 0    0    0.25 0.25 0 ……                         

0    0    ……                     0    0.25 0.25 0    0    0.25 0.25 0    0 

0    0    ……                     0    0    0    0.25 0.25 0    0    0.25 0.25

即一个4*16的矩阵。

理解一下这个4*16的矩阵规律，并引申到M*N的图像中：

1.下采样矩阵中只有两个元素，一个是0，一个跟采样系数s有关：1/s^2;(s=2)

2.矩阵具有很大的自重复性，左上角的2*8的块和右下角的2*8的块是相同的，我们称其为块‘CA’，其他位置为零。对于M*N的图像，整个下采样矩阵中这样的块‘CA’的个数是N/s个，且主对角排列，而块‘CA’的大小是s*(sM)。

3.块‘CA’同样具有重复性，以左上角2*4的块为基块，那么此时块‘CA’可以看作两个基块并肩所得，构成块‘CA’的基块称其为块‘BA’。对于M*N的图像，每个‘CA’由s个块‘BA’并肩排列构成，每隔块‘BA’的大小为s*M。

4.对于这个块‘BA’其重复性更加明显，选择左上角1*2的矩阵为新的基块‘A’，那么‘BA’就是由两个基块‘A’对角累积构成，其他位置为零。对于M*N的图像，这个块‘BA’由M/s个块‘A’对角排列构成，每隔块‘A’大小为1*s，块‘A’内的元素则都是1/s^2。

大家可以根据这个规律写一写6*6图像的3倍下采样矩阵（4*36）。

这个规律倒过来看就是之前的Matlab代码的实现规则。

其中DiagonalCat(s,A)函数的作用是将s个块‘A’主对角排列。