堆排序

本章开始介绍了堆的基本概念，然后引入最大堆和最小堆的概念。全章采用最大堆来介绍堆的操作，两个重要的操作是调整最大堆和创建最大堆，接着着两个操作引进了堆排序，最后介绍了采用堆实现优先级队列。

原地(in place)排序就是指不申请多余的空间来进行的排序，就是在原来的排序数据中比较和交换的排序。

属于原地排序的是：希尔排序、冒泡排序、插入排序、选择排序、堆排序。

1、堆

　　堆给人的感觉是一个二叉树，但是其本质是一种数组对象，因为对堆进行操作的时候将堆视为一颗完全二叉树，树种每个节点与数组中的存放该节点值的那个元素对应。所以堆又称为二叉堆，堆与完全二叉树的对应关系如下图所示：

通常给定节点i，可以根据其在数组中的位置求出该节点的父亲节点、左右孩子节点，这三个过程一般采用宏或者内联函数实现。书上介绍的时候，数组的下标是从1开始的，所有可到：PARENT(i)=i/2　　LEFT(i) = 2*i 　　RIGHT(i) = 2*i+1。

　　根据节点数值满足的条件，可以将分为最大堆和最小堆。最大堆的特性是：除了根节点以外的每个节点i，有A[PARENT(i)] >= A[i],最小堆的特性是：除了根节点以外的每个节点i，有A[PARENT(i)] >=A[i]。

　　把堆看成一个棵树，有如下的特性：

（1）含有n个元素的堆的高度是lgn。

（2）当用数组表示存储了n个元素的堆时，叶子节点的下标是floor(n/2)+1，n/2+2，……，n。

证明：假设第i个节点是堆中最后一个拥有叶子的节点，则它的节点必定是其左孩子(根据完全二叉树的定义可得) ，则LEFT(i)=2i=n，即其左孩子在数组里的存储位置为n，可得i=n/2，所以从第i+1开始的节点没有子节点，即n/2+1,n/2+2,...,n存储的节点是叶子。

（3）在最大堆中，最大元素该子树的根上；在最小堆中，最小元素在该子树的根上。

2、保持堆的性质

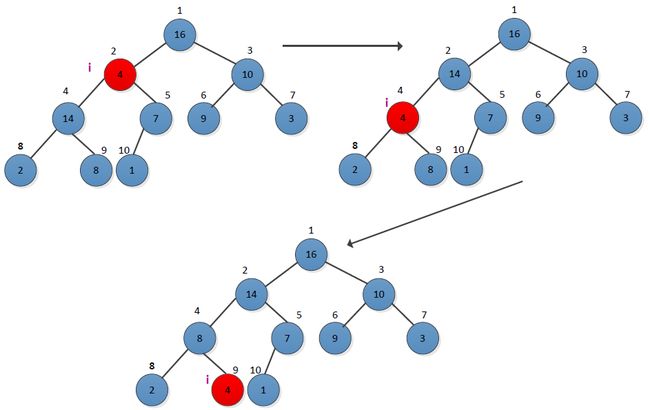
　　堆个关键操作过程是如何保持堆的特有性质，给定一个节点i，要保证以i为根的子树满足堆性质。书中以最大堆作为例子进行讲解，并给出了递归形式的保持最大堆性的操作过程MAX-HEAPIFY。先从看一个例子，操作过程如下图所示：

 

从图中可以看出，在节点i=2时，不满足最大堆的要求，需要进行调整，选择节点2的左右孩子中最大一个进行交换，然后检查交换后的节点i=4是否满足最大堆的要求，从图看出不满足，接着进行调整，直到没有交换为止。

 

3、建堆

　　建立最大堆的过程是自底向上地调用最大堆调整程序将一个数组A[1.....N]变成一个最大堆。将数组视为一颗完全二叉树，从其最后一个非叶子节点（n/2）开始调整。调整过程如下图所示：

 

4、堆排序算法
　　堆排序算法过程为：先调用创建堆函数将输入数组A[1...n]造成一个最大堆，使得最大的值存放在数组第一个位置A[1]，然后用数组最后一个位置元素与第一个位置进行交换，并将堆的大小减少1，并调用最大堆调整函数从第一个位置调整最大堆。给出堆数组A={4,1,3,16,9,10,14,8,7}进行堆排序简单的过程如下：

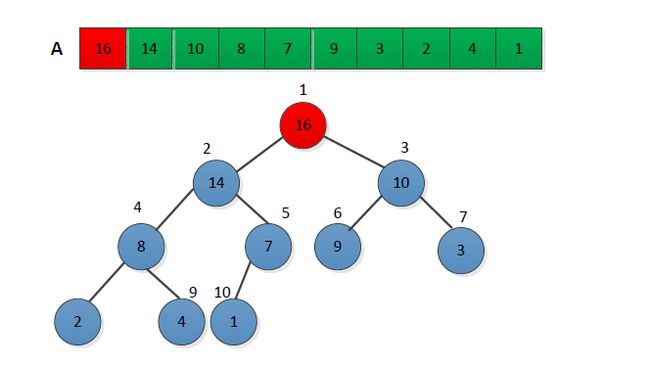
（1）创建最大堆，数组第一个元素最大，执行后结果下图：

 

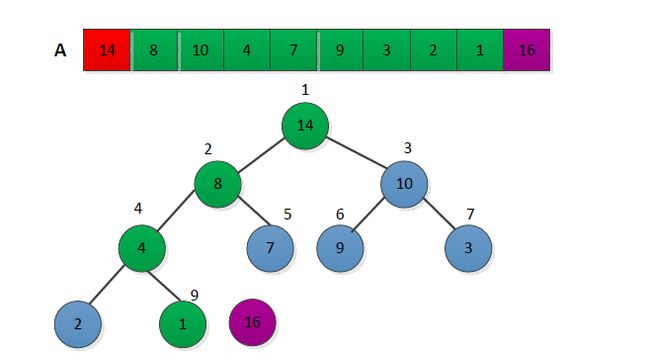
（2）进行循环，从length(a)到2，并不断的调整最大堆，给出一个简单过程如下：

从结果可以看出按照最大堆进行堆排序最终使得结果是从小到大排序（非递减的）。

堆排序算法时间复杂度：调整堆过程满足递归式T(n)<=T(2n/3)+θ(1)，有master定义可以知道T(n) = O(lgn)，堆排序过程中执行一个循环，调用最大堆调整函数，总的时间复杂度为O(nlgn）。