POJ-2488 A Knight's Journey 解题报告
Description
 Background
Background
The knight is getting bored of seeing the same black and white squares again and again and has decided to make a journey
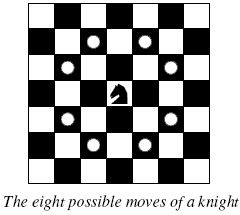
around the world. Whenever a knight moves, it is two squares in one direction and one square perpendicular to this. The world of a knight is the chessboard he is living on. Our knight lives on a chessboard that has a smaller area than a regular 8 * 8 board, but it is still rectangular. Can you help this adventurous knight to make travel plans?
Problem
Find a path such that the knight visits every square once. The knight can start and end on any square of the board.
Input
Output
If no such path exist, you should output impossible on a single line.
Sample Input
3
1 1
2 3
4 3
Sample Output
Scenario #1:
A1
Scenario #2:
impossible
Scenario #3:
A1B3C1A2B4C2A3B1C3A4B2C4
题目链接:http://poj.org/problem?id=2488
解法类型:回溯算法
解题思路:这是一道经典的回溯题,直接利用系统栈深度优先搜索即可。用一个数组标记走过的路,如果无路可走就取消标记,一直搜索下去。如果全部被标记,即搜索成功,未全部被标记则搜索失败。但需要注意输出是按字典序的顺序输出,所以要从A1出发搜索。
算法实现:
//STATUS:C++_AC_16MS_168K
#include<stdio.h>
#include<memory.h>
const int MAXN=10;
int DFS(int tot,int rear,int x,int y);
int p,q,way[MAXN*MAXN][2]={0},vis[MAXN][MAXN];
int dx[8]={-2,-2,-1,-1,1,1,2,2}, //按字典序方向行走
dy[8]={-1,1,-2,2,-2,2,-1,1};
int main()
{
// freopen("in.txt","r",stdin);
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
memset(vis,0,sizeof(vis)); //预处理
vis[0][0]=1; //标记A1已经经过
scanf("%d%d",&p,&q);
printf("Scenario #%d:\n",i);
if(DFS(p*q,1,0,0)){
for(int j=0,tot=p*q;j<tot;j++)
printf("%c%d",way[j][0]+'A',way[j][1]+1);
putchar('\n');
}
else printf("impossible\n");
if(i!=n)putchar('\n');
}
return 0;
}
int DFS(int tot,int rear,int x,int y)
{
if(rear==tot)return 1; //搜索成功
else for(int i=0;i<8;i++){
int nx=x+dx[i],ny=y+dy[i];
if(nx>=0&&nx<q && ny>=0&&ny<p && !vis[nx][ny]){
vis[nx][ny]=1; //标记为经过
if(DFS(tot,rear+1,nx,ny)){ //搜索下一个
way[rear][0]=nx,way[rear][1]=ny;
return 1;
}
vis[nx][ny]=0; //搜索不成功,标记为未经过
}
}
return 0; //搜索不成功
}
PS:今天刚从医院出来,已经有十多天没有碰过代码了,昨天下午小试身手参加了中南的月赛,结果是大跌眼镜啊,只A掉了两个。有些题在提交时因忘了注销freopen而不知道多提交了几次,可怜我在比赛时还一直郁闷怎么老是WA。。T.T...还有一道题,死磕了两小时,最后才发现题目居然看错了,结果直接悲剧。
翻了翻以前的题解,发现一般是直接贴题目上代码,以后就不能这么随便了,解题报告一定要写得规范,那就从今天开始吧。为此,我的解题报告格式为:
题目描述
解法类型
解题思路
算法实现