概率算法-均匀分布产生正态分布
大部分语言只能产生均匀分布的随机数。C语言用(double)rand()/RAND_MAX产生0到1之间均匀分布的随机数。那么如何产生正态分布的呢?
一般,一种概率分布,如果其分布函数为y=F(x),那么,y的范围是0~1,求其反函数G,然后产生0到1之间的随机数作为输入,那么输出的就是
符合该分布的随机数了:
y= G(x)
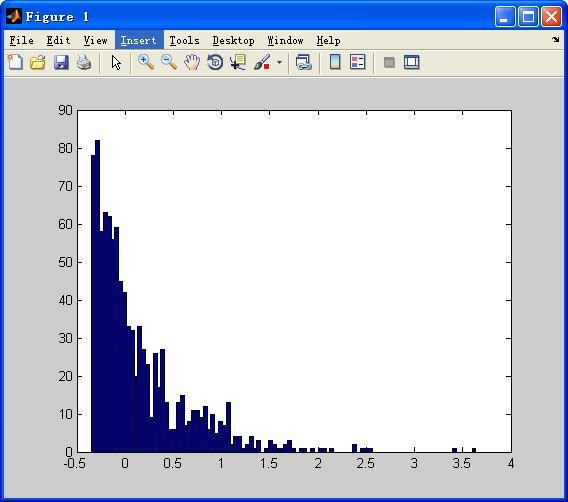
以指数分布为例,假设参数为a,那么概率密度函数为y=exp(-a);概率分布函数为y=1-exp(-a)/a。反函数为
y = -ln[(1-y)*a]/a;
MATLAB:
x=rand(1,1000);
a=2;
y=-log((1-x)*a)./a;
hist(y,100)
效果:
但是正态分布不容易这么做,因为分布函数实在有点复杂。
但是正态分布有一个特殊的性质,就是中心极限定理。其他任意分布的随机数,取大量,其均值服从高斯分布。严格的理论是这样的:
对于服从均匀分布的随机变量,只要n充分大,随机变量 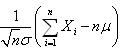 就服从均值为零,方差为1的正态分布。所以,很简单,取N个均匀分布的随机变量即可。特别的,一般可以取N=12,由于(0,1)均匀分布的均值为0.5,方差为1/12,因此代入上式,结果为 x1+x2+..+x12-6.编程的时候就很方便。
就服从均值为零,方差为1的正态分布。所以,很简单,取N个均匀分布的随机变量即可。特别的,一般可以取N=12,由于(0,1)均匀分布的均值为0.5,方差为1/12,因此代入上式,结果为 x1+x2+..+x12-6.编程的时候就很方便。
MATLAB:
n=12;
for j=1:5000
a=rand(1,n);
u=sum(a);
x(j)=(u-n*0.5);
end
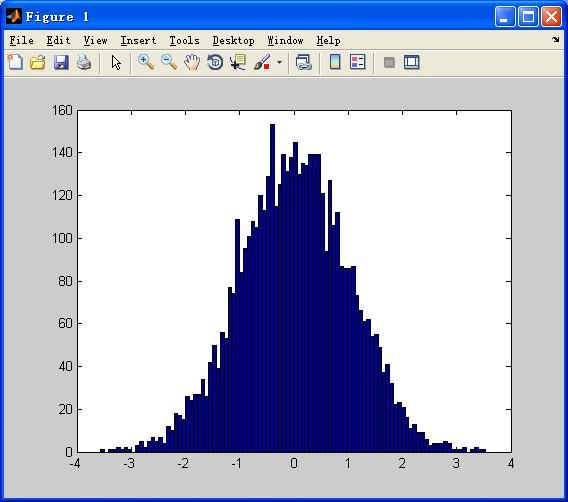
hist(x,100);
效果:
【3】最后一个办法,也是最有效的办法,是Box-Muller方法。正态分布的另一特殊性质,与瑞利分布有关。二维正态分布下,两个分量如果独立,那么他的模服从瑞利分布。瑞利分布的话,就可以通过标准的分布函数求反函数的方法求得。
MATLAB:
N=1000;
x1=rand(1,N);
x2=rand(1,N);
y1=sqrt(-2* log(x1)) .* cos(2*pi.*x2);
y2=sqrt(-2* log(x1)) .* sin(2*pi.*x2);
y=[y1,y2];
hist(y,100);