HDU 1272 小希的迷宫（并查集：判断连通且结构为树）

HDU 1272 小希的迷宫（并查集：判断连通且结构为树）

http://acm.hdu.edu.cn/showproblem.php?pid=1272

题意：

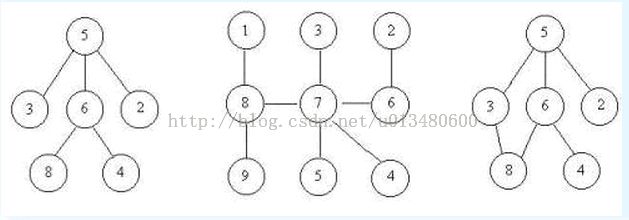
上次Gardon的迷宫城堡小希玩了很久（见Problem B），现在她也想设计一个迷宫让Gardon来走。但是她设计迷宫的思路不一样，首先她认为所有的通道都应该是双向连通的，就是说如果有一个通道连通了房间A和B，那么既可以通过它从房间A走到房间B，也可以通过它从房间B走到房间A，为了提高难度，小希希望任意两个房间有且仅有一条路径可以相通（除非走了回头路）。小希现在把她的设计图给你，让你帮忙判断她的设计图是否符合她的设计思路。比如下面的例子，前两个是符合条件的，但是最后一个却有两种方法从5到达8。 

Input

输入包含多组数据，每组数据是一个以0 0结尾的整数对列表，表示了一条通道连接的两个房间的编号。房间的编号至少为1，且不超过100000。每两组数据之间有一个空行。 
整个文件以两个-1结尾。

Output

对于输入的每一组数据，输出仅包括一行。如果该迷宫符合小希的思路，那么输出"Yes"，否则输出"No"。

分析：

        如果给的图是一个树(且输入中不能有重复边输入。如果有，也应该输出No)，那么输出Yes，否则输出No。

        一个树满足下面两个条件：只有1个连通分量且任意两点间不存在两条路。

        判断任意两点间是否存在两条路只要看已经连通的两点是否还会插入另外一条边进去？

        注意:对于输入数据0 0需要特殊判断。

AC代码(新):

#include<cstdio>
#include<set>
#include<cstring>
using namespace std;
const int maxn=100000+5;

//并查集
int fa[maxn];
int findset(int x)
{
    return fa[x]==-1? x: fa[x]=findset(fa[x]);
}
bool bind(int u,int v)
{
    int fu=findset(u);
    int fv=findset(v);
    if(fu!=fv)
    {
        fa[fu]=fv;
        return true;
    }
    return false;
}


int main()
{
    int u,v;
    while(scanf("%d%d",&u,&v)==2 && u>=0)
    {
        if(u==0 && v==0)
        {
            printf("Yes\n");
            continue;
        }

        memset(fa,-1,sizeof(fa));
        set<int> st;//st保存所有出现过得整数节点
        bool ok=true;//表示当前迷宫是否合法

        do
        {
            if(!bind(u,v)) ok=false;//连通了多余的边
            st.insert(u);
            st.insert(v);
        }while(scanf("%d%d",&u,&v)==2 && u);

        if(ok)
        {
            int cnt=0;//连通分量数目
            for(set<int>::iterator it=st.begin(); it!=st.end(); ++it)
            {
                if(*it == findset(*it) )
                    cnt++;
            }
            if(cnt>1) ok=false;
        }

        printf("%s\n",ok?"Yes":"No");
    }
    return 0;
}

 AC代码：

#include<cstdio>
#include<cstring>
using namespace std;
const int MAXN=100000+10;
int pa[MAXN];
int num[MAXN];//num[t]=i用于存储出现的数，第t个出现的数是i
int t;//总共出现了t个数
int findset(int x)
{
    if(pa[x]==0)return x;
    return pa[x]=findset(pa[x]);
}
void bind(int i,int j)
{
    int fa = findset(i);
    int fb = findset(j);
    if(fa!=fb)
        pa[fa]=fb;
}
int main()
{
    int n,m;
    while(scanf("%d%d",&n,&m)==2)
    {
        if(n==-1&&m==-1)
            break;
        if(n==0&&m==0)
        {
            printf("Yes\n");
            continue;
        }
        bool ok=true;
        t=0;
        memset(pa,0,sizeof(pa));
        memset(num,0,sizeof(num));
        while(n!=0&&m!=0)
        {
            int fa=findset(n);
            int fb=findset(m);
            num[t++]=n;
            num[t++]=m;
            if(fa!=fb)
                bind(n,m);
            else//重复边
                ok=false;
            scanf("%d%d",&n,&m);
        }
        int ans=0;
        for(int i=0;i<t;i++)
        {
            int fa = pa[num[i]];//看看有几个连通分量
            if(fa==0)
                ans++;
        }
        if(ans>1)ok=false;//连通分量的个数大于1
        if(ok)printf("Yes\n");
        else printf("No\n");
    }
    return 0;
}

new AC code：

#include<cstdio>
#include<cstring>
#include<set>
using namespace std;
const int maxn=100000+5;

int fa[maxn];
int findset(int x){ return fa[x]==-1?x:fa[x]=findset(fa[x]); }
bool bind(int u,int v)
{
    int fu=findset(u);
    int fv=findset(v);
    if(fu!=fv)
    {
        fa[fu]=fv;
        return true; //有效的合并
    }
    return false;    //重复的合并
}

int main()
{
    int u,v;
    while(scanf("%d%d",&u,&v)==2 && u!=-1)
    {
        memset(fa,-1,sizeof(fa));
        bool ok=true;
        set<int> st;
        if(u==0 && v==0)//少了这句会wrong。
        {
            printf("Yes\n");
            continue;
        }
        do
        {
            if(!bind(u,v))ok=false;//判断是否重复的合并
            st.insert(u);
            st.insert(v);
        }while(scanf("%d%d",&u,&v)==2 && u!=0);
        if(ok)
        {
            int root=0;//根节点数目
            for(set<int>::iterator it=st.begin();it!=st.end();it++)
                if(*it==findset(*it)) root++;
            if(root>1) ok=false;//至少有两个连通分量
        }
        printf("%s\n",ok?"Yes":"No");
    }
    return 0;
}