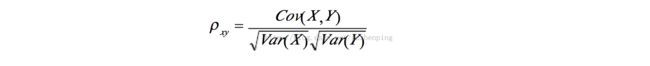算法篇----典型相关分析(CCA)理论

前言

    实际问题中，常常需要研究多个变量之间的相关关系，这个时候，可以试下典型相关分析（Canonical Correlation  Analysis）。这种算法由H·Hotelling于1936 年提出，在19世纪 70 年代臻于成熟。早期因为需要大量的矩阵计算，所以没有广泛应用。现代计算机提高了CCA的地位。

1 CCA概念

    首先，CCA研究的是两组变量X =（X1,X2,X3,......,Xn）和Y =（Y1,Y2,Y3,......,Ym）之间的相关关系。通常用相关系数衡量，如下公式：

    通过找到任意非零向量α =（α1,α2,α3,......,αn）和β =（β1,β2,β3,......,βm）将两组变量线性组合，如下：

                                                                    （注：图中的p、q请自动脑补成n、m，公式都是一样的）

   这样，CCA将研究X和Y的相关问题转变成研究U和V的相关问题，只需找到α和β使得U和V的相关系数最大即可。

顺便补几个公式:

cov是协方差，cov(X,Y) = [var(X)+var(Y)-var(X+Y)]/2

var(variance)是方差，数据是一维时候也写作D，D(X)=E(X²)-[E(X)]²

E是期望，E(X) = X1*P(X1) + X2*P(X2) + …… + Xn*P(Xn)

参考文献：http://wenku.baidu.com/link?url=z4tZlPRQOcf4lwUhzBBSwLn7UGQzW6KImBwrhM-cHkh7_e-W_wGj_qXbT71q-WeOz6IKJl0MADBTmN21lbyspEkWvc423jkywC_FGVt4WX