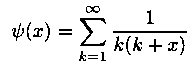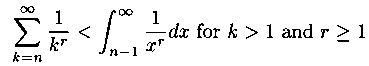Numerical Summation of a Series
Produce a table of the values of the series
Equation 1
for the 2001 values of x, x= 0.000, 0.001, 0.002, ..., 2.000. All entries of the table must have an absolute error less than 0.5e-12 (12 digits of precision). This problem is based on a problem from Hamming (1962), when mainframes were very slow by today's microcomputer standards.
Input
This problem has no input.
Output
The output is to be formatted as two columns with the values of x and y(x) printed as in the C printf or the Pascal writeln.
printf("%5.3f %16.12f/n", x, psix ) writeln(x:5:3, psix:16:12)
As an example, here are 4 acceptable lines out of 2001.
0.000 1.644934066848 ... 0.500 1.227411277760 ... 1.000 1.000000000000 ... 2.000 0.750000000000
The values of x should start at 0.000 and increase by 0.001 until the line with x=2.000 is output.
Hint
The problem with summing the sequence in equation 1 is that too many terms may be required to complete the summation in the given time. Additionally, if enough terms were to be summed, roundoff would render any typical double precision computation useless for the desired precision.
To improve the convergence of the summation process note that
Equation 2
which implies y(1)=1.0. One can then produce a series for y(x) - y(1) which converges faster than the original series. This series not only converges much faster, it also reduces roundoff loss.
This process of finding a faster converging series may be repeated to produce sequences which converge more and more rapidly than the previous ones.
The following inequality is helpful in determining how may items are required in summing the series above.
解析:
要解决此问题要着重考虑两点:精度和时间。如果单一用其中任何一个公式都面临超时或精度不够的问题。
所以,从公式2入手,将问题转换成f(x)-f(1)=(1-x)/(k*(k+1)*(k+x));而且其中f(1)=1;
这样就增大了曲线到结果值的接近速度,k从1到10000计算后的精度可以达到小数点后九位。但是仅仅这样是不够的,
还需要用公式三,将剩余项(1-x)/(k*(k+1)*(k+x)) k从10000到无穷大,即约数为(1-x)/k3,通过公式三转换
成(1-x)/(2*x12),其中x1 = 10000。
#include <iostream> #include <cstdio> using namespace std; int main() { double sum = 0; for (double x = 0.000; x <= 2.000; x += 0.001) { sum = 0; for (int k = 1; k < 10000; ++k) { sum += (1.0-x)/(k*(k+1)*(k+x)); } sum = sum + (1-x)/(2*10000*10000) + 1.0; printf("%5.3f %16.12f/n", x, sum); } return 0; }