k近邻与k-d树

k近邻

k近邻法（k nearest neighbor algorithm，k-NN）是机器学习中最基本的分类算法，在训练数据集中找到k个最近邻的实例，类别由这k个近邻中占最多的实例的类别来决定，当k=1时，即类别为最近邻的实例的类别。

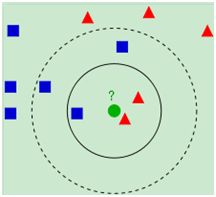
如上图所示（引自wiki），当k=3时，此时红色的个数为2，则绿色的输入实例的类别为红色的三角形，当k=5时，此时蓝色的个数为3，输入实例的类别为蓝色的四边形。
在分类过程中，k值通常是人为预先定义的常值，从上图可以看出，k值的选取对会对结果有很多的影响。大的k值可以减小噪声对分类的影响，但是和实例较远的实类会对判决起作用，通常采用交叉验证的方式来选取最优的k值。
通常实类间的距离通常采用欧氏距离，这主要面向的是连续的特征变量，对于文本分类问题，可以采用汉明距离（Hamming distance），定义为两个字符串对应位置的不同字符的个数。对距离的度量很多，往往按照应用来决定。

k近邻法的最简单的实现就是线性扫描，当训练集的数据很大，特征的维度很高的时候，计算量就会过于巨大，可以通过建立k-d tree进行快速搜索k近邻。

k-d树

k-d tree是一颗平衡二叉树，kd代表k-dimension，每个节点即为一个k维的点。每个非叶节点可以想象为一个分割超平面，用垂直于坐标轴的超平面将空间分为两个部分，这样递归的从根节点不停的划分，直到没有实例为止。

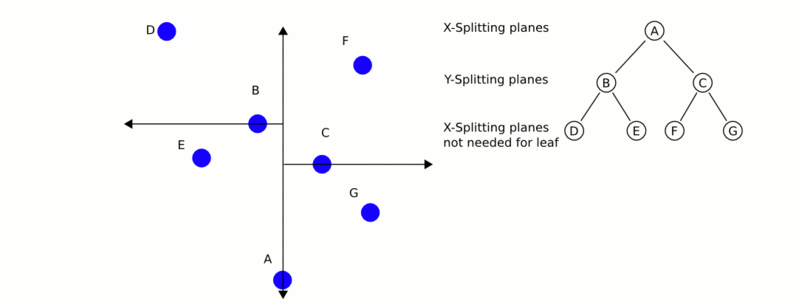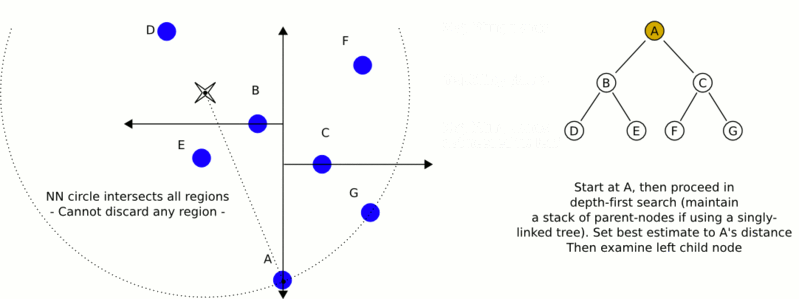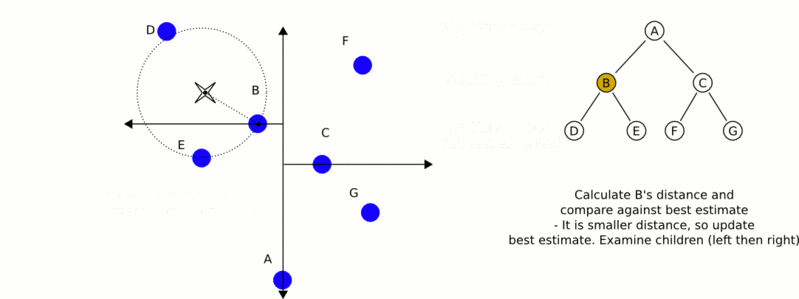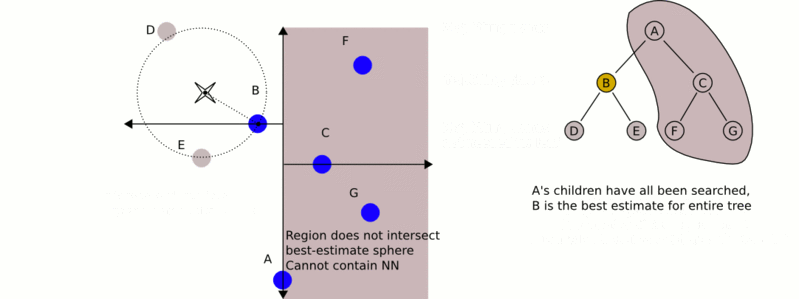
经典的构造k-d tree的规则如下：
1、随着树的深度增加，循环的选取坐标轴，作为分割超平面的法向量。对于3-d tree来说，根节点选取x轴，根节点的孩子选取y轴，根节点的孙子选取z轴，根节点的曾孙子选取x轴，这样循环下去。
2、每次均为所有对应实例的中位数的实例作为切分点，切分点作为父节点，左右两侧为划分的作为左右两子树。
对于n个实例的k维数据来说，建立kd-tree的时间复杂度为O(k*n*logn)。

例如存在6个实例点，分别为(2,3), (5,4), (9,6), (4,7), (8,1), (7,2)，下图（引自wiki）为平面对应的切分和对应的k-d tree。

                      

以最近邻搜索（nearest neighbor search（NN））算法为例，说明对kd-tree进行搜索的过程。首先从根节点出发找到包含目标点的叶节点，目标点的最近邻一定在以目标点为中心，并通过当前叶节点的超球体内部，然后从该叶节点出发，依次回退到父节点，如果父节点的另一子节点的区域与超球体相交，则到该区域继续查找，不断的查找与目标点最近邻的节点，直到不能查找最近邻的节点为止。在实例随机分布的情况下，找到最近邻的时间复杂度为O(logn)。在最差的情况下为O(k*N^(1-1/k))，可以看出，当维数和实例数相当的时候，近似于进行线性扫描，kd-tree更适合N≫2^k的情形。

如下图（引自wiki）为一个简单的NNS查找示例：

改进的方案包括一些近似算法，如在实际应用中的BBF(best-bin-first search)算法，源代码可以参见相关的SIFT源码实现。
在经典的SIFT算法中，SIFT特征点的维度为128，进行特征匹配的时候，对其中一幅图像的特征点建立k-d tree，SIFT特征点匹配为了消除误匹配点，需要找到2个最近邻的特征点，此时即为k=2，采用BBF算法从k-d tree中找出2-NN，并对两个距离进行比较，当二者相差较大才接受最近邻点为匹配点。

k近邻法也可应用到文本分类问题，在文本特征通常采用TF*IDF，对特征数据一般都会要求对数据进行规则化处理，包括进行SIFT特征的规则化。

参考

http://en.wikipedia.org/wiki/Nearest_neighbor
http://en.wikipedia.org/wiki/Kd_tree