【基于贪心的树型动态规划】【NOI2007】追捕盗贼

问题描述
魔法国度 Magic Land 里最近出现了一个大盗 Frank,他在 Magic Land 四处作案,专门窃取政府机关的机密文件(因而有人怀疑 Frank 是敌国派来的间谍)。
为了捉住 Frank,Magic Land 的安全局重拳出击!
Magic Land 由 N 个城市组成,并且这 N 个城市又由恰好 N-1 条公路彼此连接起来,使得任意两个城市间都可以通过若干条公路互达。从数据结构的角度我们也可以说,这 N 个城市和 N-1 条公路形成了一棵树。
例如,下图就是 Magic Land 的一个可能格局(4 个城市用数字编号,3 条公路用字母编号):

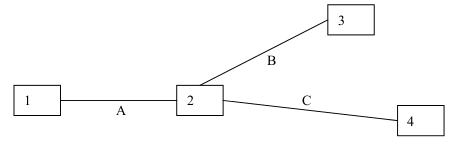
大盗 Frank 能够在公路上以任意速度移动。比方说,对于上图给出的格局,在 0.00001 秒钟内(或者任意短的一段时间内),Frank 就可以从城市 1 经过城市 2 到达城市 4,中间经过了两条公路。想要生擒 Frank 困难重重,所以安全局派出了经验丰富的警探,这些警探具有非凡的追捕才能:
1. 只要有警探和 Frank 同处一个城市,那么就能够立刻察觉到Frank,并且将其逮捕。
2. 虽然 Frank 可以在公路上以任意快的速度移动,但是如果有警探和 Frank 在同一条公路上相遇,那么警探也可以立刻察觉到 Frank 并将其逮捕。
安全局完全不知道 Frank 躲在哪个城市,或者正在哪条公路上移动,所以需要制定一个周密的抓捕计划,计划由若干步骤组成。在每一步中,可以做如下几件事中的一个:
1. 在某个城市空降一位警探。警探可以直接从指挥部空降到 Magic Land 的任意一个城市里。此操作记为“L x”,表示在编号为 x 的城市里空降一位警探。耗时 1 秒。
2. 把留在某个城市里的一位警探直接召回指挥部。以备在以后的步骤中再度空降到某个城市里。此操作记为“B x”。表示把编号为 x 的城市里的一位警探召回指挥部。耗时 1 秒。
3. 让待在城市 x 的一位警探沿着公路移动到城市 y,此操作记为“M x y”。耗时 1 秒。当然,前提是城市 x 和城市 y 之间有公路。如果在警探移动的过程中,大盗 Frank 也在同一条公路上,那么警探就抓捕到了Frank。
现在,由你来制定一套追捕计划,也就是给出若干个步骤,需要保证:无论大盗 Frank 一开始躲在哪儿,也无论 Frank 在整个过程中如何狡猾地移动(Frank大盗可能会窃取到追捕行动的计划书,所以他一定会想尽办法逃避),他一定会被缉拿归案。希望参与的警探越少越好,因为经验丰富的警探毕竟不多。
例如对于前面所给的那个图示格局,一个可行的计划如下:
1. L 2 在城市 2 空降一位警探。注意这一步完成之后,城市 2 里不会有 Frank,否则他将被捉住。
2. L 2 再在城市 2 空降一位警探。
3. M 2 1 让城市 2 的一位警探移动到城市 1。注意城市 2 里还留有另一位警探。这一步完成之后,城市 1 里不会有 Frank,公路 A 上也不会有 Frank。也就是说,假如 Frank 还没有被逮捕,那么他只能是在城市 3 或城市 4 里,或者公路 B 或公路 C 上。
4. B 1 召回城市 1 的一位警探。注意虽然召回了这位警探,但是由于我们始终留了一位警探在城市 2 把守,所以 Frank 仍然不可能跑到城市 1 或者是公路 A 上。
5. L 3 在城市 3 空降一位警探。注意这一步可以空降在此之前被召回的那位警探。这一步完成之后,城市 3 里不会有 Frank,否则他会被捉住。
6. M 3 2 让城市 3 里的一位警探移动到城市 2。这一步完成之后,如果 Frank 还没有被捉住,那他只能是在公路 C 上或者城市 4 里。注意这一步之后,城市 2 里有两位警探。
7. M 2 4 让城市 2 里的一位警探移动到城市 4。这一步完成之后,Frank 一定会被捉住,除非他根本就没来 Magic Land。这个计划总共需要 2 位警探的参与。可以证明:如果自始至终只有 1 名或者更少的警探参与,则 Frank 就会逍遥法外。
你的任务很简单:对于一个输入的 Magic Land 的格局,计算 S,也就是为了
追捕 Frank 至少需要投入多少位警探,并且给出相应的追捕计划步骤。
输入文件
输入文件给出了 Magic Land 的格局。
第一行一个整数 N,代表有 N 个城市,城市的编号是 1~N。
接下来 N-1 行,每行有两个用空格分开的整数 xi,yi,代表城市 xi,yi 之间有公路相连。保证 1≤xi,yi≤N
输出文件
向输出文件输出你所给出的追捕计划。
第一行请输出一个整数 S,代表追捕计划需要多少位警探。
第二行请输出一个整数 T,代表追捕计划总共有多少步。
接下来请输出 T 行,依次描述了追捕计划的每一步。每行必须是以下三种形式之一:
“L x”,其中 L 是大写字母,接着是一个空格,再接着是整数 x,代表在城市 x 空降一位警探。你必须保证 1≤x≤N。
“B x”,其中 B 是大写字母,接着是一个空格,再接着是整数 x,代表召回城市 x 的一位警探。你必须保证 1≤x≤N,且你的计划执行到这一步之前,城市 x 里面确实至少有一位警探。
“M x y”,其中 M 是大写字母,接着是一个空格,再接着是整数 x,再跟一个空格,最后一个是整数 y。代表让城市 x 的一位警探沿着公路移动到城市 y。你必须保证 1≤x, y≤N,且你的计划执行到这一步之前,城市 x 里面确实至少有一位警探,且城市 x, y 之前确实有公路。
必须保证输出的 S 确实等于追捕计划中所需要的警探数目。
样例输入
4
1 2
3 2
2 4
样例输出
2
7
L 2
L 2
M 2 1
B 1
L 3
M 3 2
M 2 4
评分标准
对于任何一个测试点:
如果输出的追捕计划不合法,或者整个追捕计划的步骤数 T 超过了 20000,或者追捕计划结束之后,不能保证捉住 Frank,则不能得分。
否则,用你输出的 S 和我们已知的标准答案 S*相比较:
1. 若 S<S*,则得到 120%的分。
2. 若 S=S*,则得到 100%的分。
3. 若 S*<S≤S*+2,则得到 60%的分。
4. 若 S*+2<S≤S*+4,则得到 40%的分。
5. 若 S*+4<S≤S*+8,则得到 20%的分。
6. 若 S>S +8,则得到 10%的分。
数据规模和约定
输入保证描述了一棵连通的 N 结点树,1≤N≤1 000。

虽然这是一个不完美的算法，但是也不失为一个优秀且性价比很高的算法。

首先要利用树的性质——每个点都是割点即每个度大于1的点（即除叶结点和只有一个子树的根结点以外的所有点）都可以把树分成若干个连通块。于是只要占住树根就可以递归进行将所有子树分别处理。

用f[u]表示占领整棵u为根的子树需要的最多警察数。
 1) 若u为叶结点f[u] = 1。
 2) 设val = max{f[v]} (v ∈ child(u))。
   1˚ 若u的所有子节点中，有且只有一个v满足f[v] = val，则f[u] = val；
   2˚ 若u的所有子节点中，有多个v满足f[v] = val，则f[u] = val + 1。

所以枚举所有的根，取一个f值最小的作为总根。（其它子节点由于时间的限制就只有不管了，这就是此算法得不到满分的原因。）

那么实现具体方案时，先将根控制住，再解决非关键链（只把其中一个f值最大的看作关键链，其他的都为非关键链），最后解决关键链（此时占据在根上的警察就可以移动了）。若遇到叶结点，则直接收回警察。
代码：

/**********************************\
 * @prob: NOI2007 catch           *
 * @auth: Wang Junji              *
 * @stat: 96分                    *
 * @date: May. 30th, 2012         *
 * @memo: 基于贪心的树型动态规划      *
\**********************************/
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <cstring>
#include <string>

const int maxN = 1010, maxCMD = 100010;

struct CMD
{
    int u, v; CMD() {} CMD(int u, int v): u(u), v(v) {}
    void print()
    {
        if (!u) printf("L %d", v);
        else if (!v) printf("B %d", u);
        else printf("M %d %d", u, v);
        return;
    }
} cmd[maxCMD], res[maxCMD];
struct Edge
{
    int v; Edge *next; Edge() {}
    Edge(int v, Edge *next): v(v), next(next) {}
} *edge[maxN]; int f[maxN], n, cnt, res_cnt, ans;

void Dp(int u, int Last)
{
    int ch = 0, cnt_max = 0, Max = 0, v;
    for (Edge *p = edge[u]; p; p = p -> next) if ((v = p -> v) - Last)
    {
        Dp(v, u);
        if (f[v] == Max) ++cnt_max;
        if (f[v] > Max) cnt_max = 1, Max = f[v];
        ++ch;
    }
    f[u] = cnt_max > 1 ? Max + 1 : Max;
    if (!ch) f[u] = 1; return;
}

void Dfs(int u, int Last, int D)
{
    int ch = 0, cnt_max = 0, Max = 0, pos = 0, v;
    for (Edge *p = edge[u]; p; p = p -> next) if ((v = p -> v) - Last)
    {
        Dfs(v, u, 0);
        if (f[v] == Max) ++cnt_max;
        if (f[v] > Max) cnt_max = 1, Max = f[v], pos = v;
        ++ch;
    }
    if (D)
    {
        if (!ch) {cmd[cnt++] = CMD(u, 0); return;}
        for (Edge *p = edge[u]; p; p = p -> next)
        if ((v = p -> v) - Last && v - pos)
        {
            cmd[cnt++] = CMD(0, u);
            cmd[cnt++] = CMD(u, v);
            Dfs(v, u, 1);
        }
        cmd[cnt++] = CMD(u, pos);
        Dfs(pos, u, 1);
    }
    f[u] = cnt_max > 1 ? Max + 1 : Max;
    if (!ch) f[u] = 1; return;
}

int main()
{
    freopen("catch.in", "r", stdin);
    freopen("catch.out", "w", stdout);
    scanf("%d", &n);
    for (int i = 1; i < n; ++i)
    {
        int u, v; scanf("%d%d", &u, &v);
        edge[u] = new Edge(v, edge[u]);
        edge[v] = new Edge(u, edge[v]);
    }
    int S = 1; ans = 0x3f3f3f3f;
    for (int s = 1; s < n + 1; ++s)
    {
        Dp(s, 0);
        if (f[s] < ans) ans = f[s], S = s;
    }
    cmd[cnt = 0, cnt++] = CMD(0, S); Dfs(S, 0, 1);
    while (cnt && !cmd[cnt - 1].v) --cnt;
    printf("%d\n%d", ans, cnt);
    for (int i = 0; i < cnt; ++i) printf("\n"), cmd[i].print();
    return 0;
}