HDU-4409 Family Name List LCA求解,TC+DFS || tarjan
题目:http://acm.hdu.edu.cn/showproblem.php?pid=4409
题意:就是要你求LCA。
这个题目是很典型的LCA问题,常见的有在线的TC+RMQ算法,离线的targan算法。算法的描述自己写太麻烦了,摘抄别人的(—,—):
在线算法DFS+TC描述(思想是:将树看成一个无向图,u和v的公共祖先一定在u与v之间的最短路径上):
(1)DFS:从树T的根开始,进行深度优先遍历(将树T看成一个无向图),并记录下每次到达的顶点。第一个的结点是root(T),每经过一条边都记录它的端点。由于每条边恰好经过2次,因此一共记录了2n-1个结点,用E[1, ... , 2n-1]来表示。
(2)计算R:用R[i]表示E数组中第一个值为i的元素下标,即如果R[u] < R[v]时,DFS访问的顺序是E[R[u], R[u]+1, …, R[v]]。虽然其中包含u的后代,但深度最小的还是u与v的公共祖先。
(3)RMQ:当R[u] ≥ R[v]时,LCA[T, u, v] = RMQ(L, R[v], R[u]);否则LCA[T, u, v] = RMQ(L, R[u], R[v]),计算RMQ。
由于RMQ中使用的TC算法是在线算法,所以这个算法也是在线算法。
【举例说明】
T=<V,E>,其中V={A,B,C,D,E,F,G},E={AB,AC,BD,BE,EF,EG},且A为树根。则图T的DFS结果为:A->B->D->B->E->F->E->G->E->B->A->C->A,要求D和G的最近公共祖先, 则LCA[T, D, G] = RMQ(L, R[D], R[G])= RMQ(L, 3, 8),L中第4到7个元素的深度分别为:1,2,3,3,则深度最小的是B。
离线算法(Tarjan算法)描述:
所谓离线算法,是指首先读入所有的询问(求一次LCA叫做一次询问),然后重新组织查询处理顺序以便得到更高效的处理方法。Tarjan算法是一个常见的用于解决LCA问题的离线算法,它结合了深度优先遍历和并查集,整个算法为线性处理时间。
Tarjan算法是基于并查集的,利用并查集优越的时空复杂度,可以实现LCA问题的O(n+Q)算法,这里Q表示询问 的次数。更多关于并查集的资料,可阅读这篇文章:《数据结构之并查集》。
同上一个算法一样,Tarjan算法也要用到深度优先搜索,算法大体流程如下:对于新搜索到的一个结点,首先创建由这个结点构成的集合,再对当前结点的每一个子树进行搜索,每搜索完一棵子树,则可确定子树内的LCA询问都已解决。其他的LCA询问的结果必然在这个子树之外,这时把子树所形成的集合与当前结点的集合合并,并将当前结点设为这个集合的祖先。之后继续搜索下一棵子树,直到当前结点的所有子树搜索完。这时把当前结点也设为已被检查过的,同时可以处理有关当前结点的LCA询问,如果有一个从当前结点到结点v的询问,且v已被检查过,则由于进行的是深度优先搜索,当前结点与v的最近公共祖先一定还没有被检查,而这个最近公共祖先的包涵v的子树一定已经搜索过了,那么这个最近公共祖先一定是v所在集合的祖先。
【举例说明】
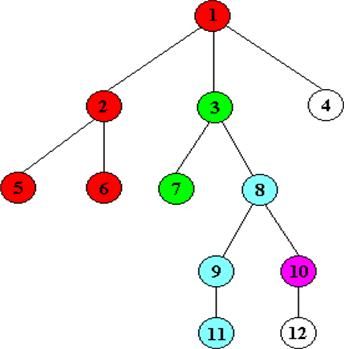
根据实现算法可以看出,只有当某一棵子树全部遍历处理完成后,才将该子树的根节点标记为黑色(初始化是白色),假设程序按上面的树形结构进行遍历,首先从节点1开始,然后递归处理根为2的子树,当子树2处理完毕后,节点2, 5, 6均为黑色;接着要回溯处理3子树,首先被染黑的是节点7(因为节点7作为叶子不用深搜,直接处理),接着节点7就会查看所有询问(7, x)的节点对,假如存在(7, 5),因为节点5已经被染黑,所以就可以断定(7, 5)的最近公共祖先就是find(5).ancestor,即节点1(因为2子树处理完毕后,子树2和节点1进行了union,find(5)返回了合并后的树的根1,此时树根的ancestor的值就是1)。有人会问如果没有(7, 5),而是有(5, 7)询问对怎么处理呢? 我们可以在程序初始化的时候做个技巧,将询问对(a, b)和(b, a)全部存储,这样就能保证完整性。 4、 总结 LCA和RMQ问题是两个非常基本的问题,很多复杂的问题都可以转化这两个问题解决,这两个问题在ACM编程竞赛中遇到的尤其多。这两个问题的解决方法中用到很多非常基本的数据结构和算法,包括并查集,深度优先遍历,动态规划等。
My code:
//STATUS:C++_AC_156MS_10876KB
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<string>
#include<vector>
#include<queue>
#include<stack>
#include<math.h>
#include<map>
#include<set>
using namespace std;
#define LL __int64
#define pii pair<int,int>
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
const int MAX=30010,INF=200000000;
const double esp=1e-6;
int min(int x,int y){return x<y?x:y;}
struct Node{
char name[62];
int fa,cou,level;
}man[MAX];
struct cmp{
bool operator()(const int i,const int j){
int t=strcmp(man[i].name,man[j].name);
if(t<0)return 1;
else return 0;
}
};
int now[MAX],num[MAX],d[MAX<<1],e[MAX<<1],r[MAX],pow2[35];
int f[MAX<<1][16];
int n,m,k,dis;
map<string,int> shi;
set<int,cmp> q[MAX];
inline int getlevel(char *a){
int i=0;
while(a[i]=='.')i++;
return i;
}
int input(){
int i,j,t;
scanf("%s",man[0].name);
man[0].fa=-1;
for(i=1;i<n;i++){
scanf("%s",man[i].name);
t=man[i].level=getlevel(man[i].name);
shi[man[i].name+t]=i;
now[t--]=i;
man[i].fa=now[t];
man[now[t]].cou++;
q[now[t]].insert(i);
}
return 1;
}
int DFS(int cur,int deep){
d[dis]=deep;
e[dis]=cur;
r[cur]=dis++;
set<int,cmp>::iterator it;
for(it=q[cur].begin();it!=q[cur].end();it++){
num[k++]=*it;
DFS(*it,deep+1);
d[dis]=deep;
e[dis++]=cur;
}
return 1;
}
int min2(int i,int j){
return d[i]<d[j]?i:j;
}
int st(){
int i,j,len=(n<<1)-1;
for(i=0;i<31;i++)
pow2[i]=1<<i;
for(i=0;i<len;i++)
f[i][0]=i;
for(j=1;pow2[j]-1<len;j++){
for(i=0;i+pow2[j]-1<len;i++){
f[i][j]=min2(f[i][j-1],f[i+(1<<(j-1))][j-1]);
}
}
return 1;
}
int rmq(int x,int y){
int k=log((double)(y-x+1))/log(2.0);
return min2(f[x][k],f[y-pow2[k]+1][k]);
}
int output()
{
int i,j,fa1,fa2;
char op[2],s1[62],s2[62];
k=dis=0;
DFS(0,0);
st();
scanf("%d",&m);
while(m--)
{
scanf("%s",op);
if(op[0]!='L'){
if(op[0]=='b'){
scanf("%s",s1);
fa1=man[shi[s1]].fa;
if(fa1<0)
printf("1\n");
else
printf("%d\n",man[fa1].cou);
}
else{
scanf("%s%s",s1,s2);
fa1=man[shi[s1]].fa,fa2=man[shi[s2]].fa;
if(r[fa1]<=r[fa2])
fa1=e[rmq(r[fa1],r[fa2])];
else fa1=e[rmq(r[fa2],r[fa1])];
printf("%s\n",man[fa1].name+man[fa1].level);
}
}
else {
printf("%s\n",man[0].name);
int i;
for(i=0;i<n-1;i++)
printf("%s\n",man[num[i]].name);
}
}
return 1;
}
int main()
{
// freopen("in.txt","r",stdin);
while(~scanf("%d",&n) && n)
{
memset(man,0,sizeof(man));
for(int i=0;i<=n;i++)
q[i].clear();
shi.clear();
input();
output();
}
return 0;
}