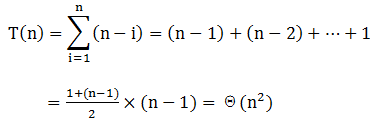算法学习笔记----确定n个元素的任何排列中逆序对的数目

题目：设A[1...n]是一个包含n个不同数的数组。如果在i<j的情况下，有A[i]>A[j]，则（i,j）就称为A中的一个逆序对（inversion）。给出一个算法，它能用Θ(nlgn)的最坏情况运行时间，确定n个元素的任何排列中逆序对的数目。

解题思路：

 ①比较直观的方法是循环从数组中取出一个元素k，然后从k之后的元素中找到比k小的元素个数，最后统计所有的个数即为排列中逆序对的数目。从数组中取元素的次数为n，每次取出一个元素后，需要遍历（n-i）次（i为当前元素的位置），其时间复杂度为：

  时间复杂度为Θ(n^2)，不符合题目要求。

  ②利用插入排序的方式来解决。对数组用插入排序来做升序排列时，如果有元素需要移动，则每次移动时都相当于是找到了一个逆序对，因此插入队列中移动元素的次数，也就是排列中逆序对的数量。但插入排序的时间复杂度为Θ(n^2)，不符合题目要求。

  ③利用归并排序的递归思想来解决，首先对数组的从中间分开，然后分别计算左半部和右半部的逆序对数，假设和为S，最后在合并过程中如果左半部的元素小于右半部的元素，则相当于是找到了一个逆序对，假设合并时找到的逆序对数为S'，则总的逆序对数位S+S'。归并排序的时间复杂度为Θ(nlgn)，符合题目要求。其代码实现如下：

#include <stdio.h>
#include <errno.h>

#ifndef INT_MAX
#define INT_MAX		((int)(~0U>>1))
#endif

#define ARRAY_SIZE(__s) (sizeof(__s) / sizeof(__s[0]))

static void merge_inversions(int *a, int start, int mid, int end, int *count)
{
    int nl = mid - start + 1;
    int nr = end - mid;
    int sentinel = INT_MAX;
    int left[nl + 1], right[nr + 1];
    int i, j, k = start;
    
    for (i = 0; i < nl; ++i) {
        left[i] = a[k++];
    }
    /* Set sentinel */
    left[i] = sentinel;
    
    for (j = 0; j < nr; ++j) {
        right[j] = a[k++];
    }
    /* Set sentinel */
    right[j] = sentinel;
    
    i = j = 0;
    for (k = start; k <= end; ++k) {
        if (left[i] <= right[j]) {
            a[k] = left[i++];
        } else {
            (*count)++;
            a[k] = right[j++];
        }
    }
}

static void count_versions(int *a, int start, int end, int *count)
{
    int mid;
    
    if ((start >= 0) && (start < end)) {
        mid = (start + end) /2 ;
        
        count_versions(a, start, mid, count);
        count_versions(a, mid + 1, end, count);
        
        merge_inversions(a, start, mid, end, count);
    }
}

int main(void)
{
    //int source[] = { 7, 5, 2, 4, 6, 1, 5, 3};
    int source[] = {2, 3, 8, 6, 1};
    int count = 0;
    
    count_versions(source, 0, ARRAY_SIZE(source) - 1, &count);
    
    printf("Reversions: %d.\n", count);

    return 0;
}