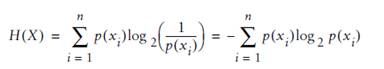人工智能算法—决策树
文/腾讯soso 林世飞
决策树方法最早产生于上世纪60年代,到70年代末。由J Ross Quinlan提出了ID3算法,此算法的目的在于减少树的深度。但是忽略了叶子数目的研究。C4.5算法在ID3算法的基础上进行了改进,对于预测变量的缺值处理、剪枝技术、派生规则等方面作了较大改进,既适合于分类问题,又适合于回归问题
这里 介绍其基本原理 和一个实验例子。
先介绍2个算法:
算法一:熵(entropy)
熵(entropy)指的是体系的混乱的程度,当我们尝试把混合集合A={B1,B2,C1,C2…..} (其中Bx表示一个类别的元素,Cx表示另外一个) 划分为2个集合 M、N(即决策树的2个分支时候),比较好的划分是 M 里面都是 Bx,N里面都是Cx,这时候我们需要一个函数对 划分以后 的 集合进行评估,看看是否纯度 够“纯”。如果很纯,很有序,熵就是0.
理解该公式: p(xi) 越平均,系统约混乱,如果系统只有2个元素x1、x2,x1出现概率是0.5,x2出现概率也是0.5,即p(x1) =0.5 p(x2) =0.5 ,这时公式计算结果为1; p(xi)如果比较不平均,比如p(x2) =1,那就是系统很确定,一点都不混乱,肯定是x2构成,这时熵计算结果就是0.
这个规律刚刚好是 log 函数特点 过(1,0)这个点(见下图),我想这个就是克劳德·艾尔伍德·香农设计这个公式选择log函数的道理。
用python 实现就是 :
def entropy(l):
from math import log
#函数编程语法,定义一个函数
log2=lambda x:log(x)/log(2)
total=len(l)
counts={}
#统计每个类型出现格式
for item in l:
counts.setdefault(item,0)
counts[item]+=1
ent=0
for i in counts:
p=float(counts[i])/total #计算概率
ent-=p*log2(p) #熵计算
return ent
算法二:除了 熵,还有一个衡量一个集合是否混乱的方法叫 Gini Impurity (基尼不纯度)方法。
公式如下:
公式基本上也符合以上 熵的 规律: 集合越纯 值越小,如果只有2个元素时候,每个元素出现概率就是0.5,这时 I = 0.5*0.5 +0.5*0.5 =0.5
0.5*0.5 # 我的理解是 K1(出现概率0.5) 被当做 其他Kx的概率(出现概率0.5)
Python 实现如下:
# 去重 统计每个出现次数
def uniquecounts(rows):
results={}
for row in rows:
# The result is the last column
r=row[len(row)-1]
if r not in results: results[r]=0
results[r]+=1
return results
def giniimpurity(rows):
total=len(rows)
counts=uniquecounts(rows)
imp=0
for k1 in counts:
# k1 的概率
p1=float(counts[k1])/total
for k2 in counts:
if k1==k2: continue
# k2 的概率
p2=float(counts[k2])/total
# 我的理解是 K1 被当做 其他Kx的概率
imp+=p1*p2
return imp
现在开始介绍决策树:
决策树树节点定义:
class decisionnode:
def __init__(self,col=-1,value=None,results=None,tb=None,fb=None):
self.col=col #第几个列 即因子
self.value=value #判断值
self.results=results #结果集合
self.tb=tb #左右树
self.fb=fb
#构建决策树的过程,scoref 就是前面衡量 集合混乱 程度的2个算法的函数之一
def buildtree(rows,scoref=entropy):
if len(rows)==0: return decisionnode()
current_score=scoref(rows)
# 最佳划分
best_gain=0.0
best_criteria=None
best_sets=None
#列数
column_count=len(rows[0])-1
for col in range(0,column_count):
column_values={}
# 统计每一列可能的值
for row in rows:
column_values[row[col]]=1
#尝试每一列 每一种值 作为划分集合
for value in column_values.keys():
(set1,set2)=divideset(rows,col,value)
# Information gain 信息增益??我的理解是加权计算目前的得分,即纯度、混乱度
p=float(len(set1))/len(rows)
gain=current_score-p*scoref(set1)-(1-p)*scoref(set2)
if gain>best_gain and len(set1)>0 and len(set2)>0:
best_gain=gain
best_criteria=(col,value)
best_sets=(set1,set2)
# 创建子分支
if best_gain>0:
trueBranch=buildtree(best_sets[0])
falseBranch=buildtree(best_sets[1])
return decisionnode(col=best_criteria[0],value=best_criteria[1],
tb=trueBranch,fb=falseBranch)
else:
# 如果是叶子节点则统计这个分支的 个数
return decisionnode(results=uniquecounts(rows))
#根据某列值 划分rows 为 2个 集合
# or nominal values
def divideset(rows,column,value):
# Make a function that tells us if a row is in
# the first group (true) or the second group (false)
split_function=None
if isinstance(value,int) or isinstance(value,float):
split_function=lambda row:row[column]>=value
else:
split_function=lambda row:row[column]==value
# Divide the rows into two sets and return them
set1=[row for row in rows if split_function(row)]
set2=[row for row in rows if not split_function(row)]
return (set1,set2)
#利用一个已知树 决策过程
def classify(observation,tree):
if tree.results!=None:
return tree.results
else:
v=observation[tree.col]
branch=None
if isinstance(v,int) or isinstance(v,float):
if v>=tree.value: branch=tree.tb
else: branch=tree.fb
else:
if v==tree.value: branch=tree.tb
else: branch=tree.fb
return classify(observation,branch)
时间抽取是 web 页面 分类、抽取时候一个很重要的 课题。通常一个页面将包含多个可能代表 该页面 发表时间的 字符串,如果判断一个 包含数字的字符串是否是一个时间串 ,往往要考虑很多因素,比如 ,整个过程会比较繁琐。
这里尝试利用1099 页面 分析处理得到的162个时间串的各个属性 ,利用决策树进行学习,最终生成一个决策树 ,该决策树可以新的 时间串,根据其属性进行 判断。
以下是实验效果:
其中每一列代表 其属性值,比如 第一列含义是 该字符串是否出现在 链接中,是为ture。
生成决策树:
>>> datas=[ line.split('|')[1:] for line in file('result3') ]
>>> tree= treepredict.buildtree(datas)
对某个时间 2010-05-27 00:00:00 提取的各个特征通过这个决策树 判断是否是时间
2010-05-27 00:00:00|false|false|false|false|true|false|false|false|8825|0.971809|2|8|0|false|false|0
结论是:不是时间
>>> treepredict.classify(['false', 'false', 'false', 'false', 'true', 'false', '
false', 'false', 'false', 'false', 'false', 'false', 'false', '0', '7754','249',
'0.967919', '0.031082', '0', '0', '0', '0', '0', '2', '-1', '0', '8', '0', '0',
'0'],tree)
{'0/n': 30}
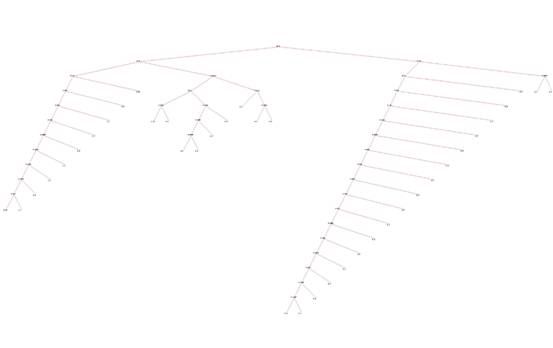
我们可以查看下 这个机器学习 产生的 决策树:
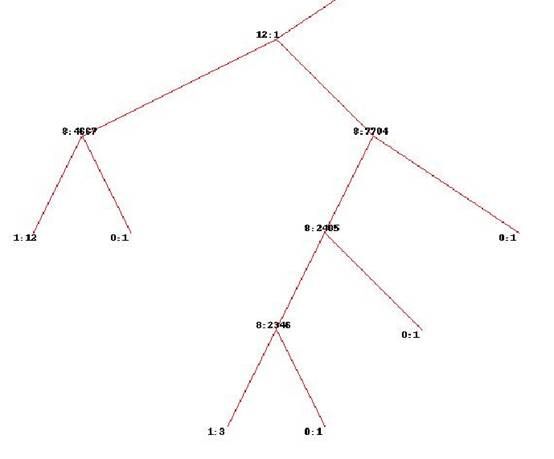
局部:
从上图可以看到 8 、10、11 列 值对于该问题决策—该串是否是时间串 起着关键作用,虽然我们可能考虑很多因素、但以下几列起着关键作用,具体含义是 块开始 、 正文的位置关系 、字符串长度等。
这个从实验数据集来看也比较正常,因为这个数据集是我的实验数据,很多列值没有精确计算,基本雷同,变化不大。换句话说,对最后决策其作用都是那些 变化比较大的列项。
以上是关于决策树原理实现和工程利用的一个例子的学习笔记,对于时间抽取是否适合利用决策树来处理,目前还没有定论和应用,这里只是利用他来帮助我们理解 在众多因素参与决策时候,哪些因素关键些,较好解释了我们决策过程,每个因子起到作用,比如有的因子其实不起作用,至少在我们的数据集中。
决策树在工程实际利用时候,可能 还要面临 树裁剪 (Decision Tree Pruning)、数据项某些维度数据缺少的问题。
什么时候使用决策树 ,本身就是一个问题。
更多内容参考
http://wiki.mbalib.com/wiki/%E5%86%B3%E7%AD%96%E6%A0%91