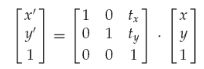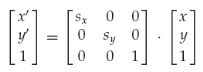Android Matrix的 pre post set方法的理解(zz)

1、http://blog.csdn.net/rav009/article/details/7763223

matrix.setScale(interpolatedTime, interpolatedTime);

matrix.preTranslate(-centerX, -centerY);

matrix.postTranslate(centerX, centerY);

经常在中心缩放的应用中看到这段代码.

preTranslate是指在setScale前,平移,postTranslate是指在setScale后平移

注意他们参数是平移的距离,而不是平移目的地的坐标!

由于缩放是以(0,0)为中心的,所以为了把界面的中心与(0,0)对齐,就要preTranslate(-centerX, -centerY),

setScale完成后,调用postTranslate(centerX, centerY),再把图片移回来,这样看到的动画效果就是activity的界面图片从中心不停的缩放了

注:centerX和centerY是界面中心的坐标

2、http://www.linuxidc.com/Linux/2012-07/65035.htm

虽说以前学习过线性代数和图形学原理，但是在实际中碰到matrix还是疑惑了好一阵子，今天通过向同事请教终于找到一点门路，特总结如下：

Matrix主要用于对平面进行缩放，平移，旋转以及倾斜操作，为简化矩阵变换，Android封装了一系列方法来进行矩阵变换，其中包括pre系列方法：preScale，preTranslate，preRotate，preSkew，set系列方法：setScale，setTranslate，setRotate，setSkew，post系列方法：postScale，postTranslate，postRotate，postSkew。

通过将变换矩阵与原始矩阵相乘来达到变换的目的，例如：

平移：

旋转：

缩放：

有一点要说明：上图中的原始矩阵为3*1的矩阵，我们可以将其扩展成3*3的矩阵，否则下文涉及到的后乘操作将不成立，甚至在后乘的时候我们可以看成是1*3的矩阵，这不影响实际的变换效果。

之前一直不理解为什么要设置pre，set和post三种变换操作，我一直认为只通过post操作即可完成所有的变换，后来通过查阅相关资料以及同事的指点，有了一些粗浅的认识，当然现在的认识仍然是模模糊糊，甚至是错误的，希望通过博客和大家分享并纠正我可能存在的错误。

pre方法表示矩阵前乘，例如：变换矩阵为A，原始矩阵为B，pre方法的含义即是A*B

post方法表示矩阵后乘，例如：变换矩阵为A，原始矩阵为B，post方法的含义即是B*A

1. matrix.preScale(0.5f, 1);   
2. matrix.preTranslate(10, 0);  
3. matrix.postScale(0.7f, 1);    
4. matrix.postTranslate(15, 0);  

等价于：

translate(10, 0) -> scale(0.5f, 1) -> scale(0.7f, 1) -> translate(15, 0)

注意：后调用的pre操作先执行，而后调用的post操作则后执行。

set方法一旦调用即会清空之前matrix中的所有变换，例如：

1. matrix.preScale(0.5f, 1);   
2. matrix.setScale(1, 0.6f);   
3. matrix.postScale(0.7f, 1);   
4. matrix.preTranslate(15, 0);  

等价于

translate(15, 0) -> scale(1, 0.6f) ->  scale(0.7f, 1)

matrix.preScale (0.5f, 1)将不起作用。

以下为个人理解，不保证一定正确：

如果通过getMatrix()得到的matrix是一个未经过任何变换的单元矩阵，或者是之前已经调用过setMatrix的matrix，那么我们可以仅使用post系列方法或者pre系列方法的其中一种来完成各种变换操作，因为此时我们仅使用pre或者post方法来定义各种变换次序。

但是如果我们得到的matrix是一个非单元矩阵，并且该matrix还未调用setMatrix应用到实际中，此时我们可能同时需要pre和post方法来实现我们所需要的变换，例如C是通过getMatrix得到的并满足之前描述的matrix，此时如果我想在现有的变换之前进行某些变换，此时只有pre方法可以做到，假如C是一个执行过postScale操作的matrix，此时我想在postScale之前进行平移，那只有调用preTranslate，这样当调用setMatrix的时候会先进行preTranslate操作，再进行postScale操作。必须这么做的前提就是先scale后translate和先translate后scale得到的是不同的变换效果。

3、http://wenku.baidu.com/view/96590cd076a20029bd642ddf.html

Matrix学习——图像的复合变化 
Matrix学习——基础知识篇幅中，我们留下一个话题：如果图像围绕着某个点P(a，b)旋转，则先要将坐标系平移到该点，再进行旋转，然后将旋转后的图像平移回到原来的坐标原点。 我们需要3步： 1. 平移——将坐标系平移到点P(a，b)；  2. 旋转——以原点为中心旋转图像；  
3. 
平移——将旋转后的图像平移回到原来的坐标原点；  
相比较前面说的图像的几何变化（基本的图像几何变化），这里需要平移平移——旋转——平移平移，这种需要多种图像的几何变化就叫做图像的复合变化。 
设对给定的图像依次进行了基本变化F1、F2、F3…..、Fn，它们的变化矩阵分别为T1、T2、T3…..、Tn，图像复合变化的矩阵T可以表示为可以表示为：：T = TnTn-1…T1。 
按照上面的原则，围绕着某个点(a，b)旋转θ的变化矩阵序列是： 
 
按照上面的公式，我们列举一个简单的例子：围绕（100，100）旋转30度(sin 30 = 0.5 ，cos 30 = 0.866) float f[]= { 0.866F,  -0.5F, 63.4F,0.5F, 0.866F,-36.6F,0.0F,    0.0F,  1.0F }; matrix = new Matrix(); matrix.setValues(f); 旋转后的图像如下： 
 
Android为我们提供了更加简单的方法，如下： Matrix matrix = new Matrix(); matrix.setRotate(30，100，100); 矩阵运行后的实际结果： 
 

与我们前面通过公式获取得到的矩阵完全一样。 
在这里我们提供另外一种方法，也可以达到同样的效果： 

float a = 100.0F,b = 100.0F; 

matrix = new Matrix(); 

matrix.setTranslate(a,b); 

matrix.preRotate(30); 

matrix.preTranslate(-a,-b); 

将在后面的篇幅中为大家详细解析 
通过类似的方法，我们还可以得到：相对点相对点P(a，b)的比例[sx,sy]变化矩阵