POJ 2464 Brownie Points II(线段树:扫描线)

POJ 2464 Brownie Points II(线段树:扫描线)

http://poj.org/problem?id=2464

题意:平面上有很多点,然后stan通过一个点画了一条竖线,ollie通过已经被该竖线穿过的点画了一条横线.现在平面被分成了4个象限了.stan获得的分数是1,3象限的点数,ollie获得的分数是2,4象限的点数.由于stan先画竖线,他可以保证在让自己可能获得的所有可能分数集合中使得画下该线后,自己可能获得的最小可能分数最大.输出该分数,并输出ollie可能获得的分数.

分析: 本题题意比较难懂.

总体流程:

其实本题就是将每个点依次作为坐标轴的原点,然后求出stan和ollie可以获得的分数.将所有的点按x坐标从小到大排序,依次认为竖线在当前x坐标上,然后依次遍历x坐标就是当前竖线x位置的这些点,以这些点为坐标轴交叉点,来分析stan和ollie可以获得的分数.此时由于是ollie后操作,所以ollie明显取它的值最大的那个点,stan只能被动的选在所有能使ollie值最大的点中,stan分数最小的值(因为我们要求stan获得的最小分数最大,所以对于同一条竖线,我们每次都去找ollie取最大的时候,stan的最小值,然后看看这个最小值是不是当前stan的最大值). 综上所述,其实就是对于一条竖线来说,找到在这条竖线不变的基础上,加上可能的横线,然后找到ollie取最大值时候,stan能取的所有值中最小的值.然后我们遍历所有可能的竖线,使得stan能取的所有最小值取最大即可.

现在的问题是:固定了坐标原点后我们如何快速的求得四个象限的点数?

首先我们要求下面5个信息:

right[i]: 第i个点正右方点的个数.(即与i点y坐标相同,但是x坐标比i点的x坐标大的数个数)

left[i]: 第i个点正左方点的个数.(即与i点y坐标相同,但是x坐标比i点的x坐标小的数个数)

large[i]:比第i个点y值要大的点的数目

(上面这两个信息可以通过将点的数组按优先y从小到大,如果y值相同就按x从小到大排序之后,获得)

up[i]:在第i个点正上方的点个数

down[i]: 在第i个点正下方的点的个数.

 

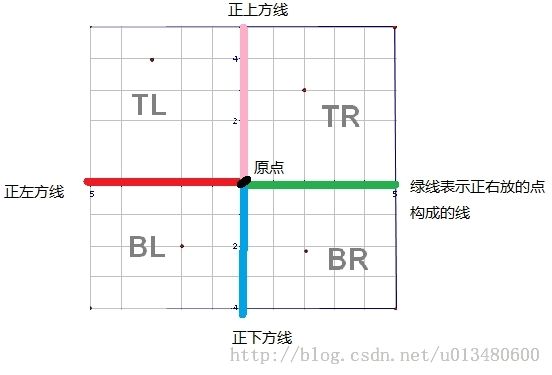
将所有点按x坐标从小到大(x相同,y从小到大)排序,维护一棵树状数组,每读入一个点就把这个点的y坐标插入树状数组里面,假设当前处理第i个点(我们先查询,再插入i点的y坐标),并把它作为原点处理.那么上图中四个区域的点为:

BL =getsum(y[i])-left[i]-down[i];

即已经读入的那些在当前点左下方的点.

TL=i-1-BL-left[i]-down[i].

因为已经读入了i-1个点(且x坐标都小于等于x[i],所以这i-1个点都在i点左边),这坐标的所有i-1个点减去BL和left和down的点就是TL的点.

TR=large[i]-TL-up[i]

BR=n-1-BL-TL-BR-left-right-up-down.

这样我们就求出了stan=BL+TR,ollie=TL+BR

然后我们看看对于当前竖线ollie是不是去最大值,如果是的话,就计算stan能取的最小值MIN_V;

然后我们根据当前竖线的MIN_V值来更新stan的(最大的)最小值,并把ollie的值保存在set中.

注意:在使用树状数组的时候,由于y坐标范围大,所以需要离散化.

当固定了竖线之后,只有一个ollie的最大值和一个与之对应的stan的最小值.然后用这两个值去更新全局stan的最大值并把ollie的最大值存取set中..

AC代码:250ms

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<set>
using namespace std;
const int MAXN = 210005;
int c[MAXN], n;
int up[MAXN], right[MAXN], left[MAXN], down[MAXN], large[MAXN];
int id[MAXN];
int lowbit(int x)
{
    return x & (-x);
}
void add(int x, int v)
{
    while(x < MAXN)
    {
        c[x] += v;
        x += lowbit(x);
    }
}
int sum(int x)
{
    int res = 0;
    while(x>0)
    {
        res += c[x];
        x -= lowbit(x);
    }
    return res;
}
struct node
{
    int x, y;
    int id;
} p[MAXN];
bool cmp1(node a, node b) //优先x坐标从小到大排序
{
    if(a.x != b.x) return a.x < b.x;
    return a.y < b.y;
}
bool cmp2(node a, node b) //优先y坐标从小到大排序
{
    if(a.y != b.y) return a.y < b.y;
    return a.x < b.x;
}
void init()
{
    for(int i = 0; i <= n; i++)
        c[i] = large[i] = left[i] = right[i] = up[i] = down[i] = 0;
}
int main()
{
    while(scanf("%d", &n) == 1 && n)
    {
        for(int i = 0; i < n; i++)
        {
            scanf("%d%d", &p[i].x, &p[i].y);
            p[i].id = i;
        }
        init();
        sort(p, p + n, cmp2); //优先y坐标排序
        for(int i = 1; i < n; i++)
        {
            if(p[i].y == p[i - 1].y)
                left[p[i].id] = left[p[i-1].id] + 1;
            if(p[n - 1 - i].y == p[n - i].y)
            {
                right[ p[n - 1 - i].id ] = right[ p[n - i].id ] + 1;
                large[p[n - 1 - i].id] = large[p[n - i].id];
            }
            else
                large[p[n - 1 - i].id] = i;
        }
        int tid = 1;
        id[p[0].id] = tid;
        for(int i = 1; i < n; i++)
        {
            if(p[i].y == p[i - 1].y)
                id[p[i].id] = tid;
            else
                id[p[i].id] = ++tid;
        }
        sort(p, p + n, cmp1); //按x坐标从小到大排序
        for(int i = 1; i < n; i++)
        {
            if(p[i].x == p[i - 1].x)
                down[p[i].id] = down[p[i - 1].id] + 1;
            if(p[n - 1 - i].x == p[n - i].x)
                up[p[n - 1 - i].id] = up[p[n - i].id] + 1;
        }
        int px = p[0].x; //当前处理竖线的坐标
        set<int> st;
        int s_min_max = 0;
        for(int i = 0; i < n; i++)
        {
            int omax = 0, smin = MAXN;
            while(i < n && p[i].x == px) //处理当前竖线上的所有点
            {
                int yid = id[p[i].id]; //离散化后的坐标
                int BL = sum(yid) - left[p[i].id] - down[p[i].id];
                int TL = i - sum(yid);
                int TR = large[p[i].id] - TL - up[p[i].id];
                int BR = n - 1 - BL - TL - TR - left[p[i].id] - right[p[i].id] - up[p[i].id] - down[p[i].id];
                add(yid, 1);
                int ollie = TL + BR;
                if(ollie > omax)
                {
                    omax = ollie;
                    smin = BL + TR;
                }
                else if(ollie == omax)
                {
                    smin = min(smin, TR+BL);
                }
                i++;
            }
            if(i < n) px = p[i--].x;
            if(smin > s_min_max)
            {
                s_min_max = smin;
                st.clear();
                st.insert(omax);
            }
            else if(smin == s_min_max)
            {
                st.insert(omax);
            }
        }
        printf("Stan: %d; Ollie:", s_min_max);
        set<int>::iterator it;
        for(it = st.begin(); it != st.end(); it++)
            printf(" %d", *it);
        printf(";\n");
    }
    return 0;
}