【线段树】【NOI2007】项链工厂

问题描述
T 公司是一家专门生产彩色珠子项链的公司,其生产的项链设计新颖、款式多样、价格适中,广受青年人的喜爱。最近 T 公司打算推出一款项链自助生产系统,使用该系统顾客可以自行设计心目中的美丽项链。
该项链自助生产系统包括硬件系统与软件系统,软件系统与用户进行交互并控制硬件系统,硬件系统接受软件系统的命令生产指定的项链。该系统的硬件系统已经完成,而软件系统尚未开发,T 公司的人找到了正在参加全国信息学竞赛的你,你能帮助 T 公司编写一个软件模拟系统吗?
一条项链包含 N 个珠子,每个珠子的颜色是 1, 2, ..., c 中的一种。项链被固定在一个平板上,平板的某个位置被标记位置 1,按顺时针方向其他位置被记为2,3,...,N。

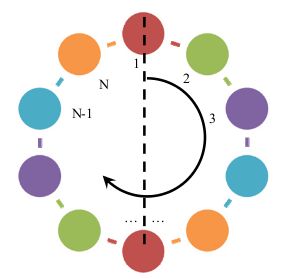
你将要编写的软件系统应支持如下命令:

输入文件
输入文件第一行包含两个整数 N, c,分别表示项链包含的珠子数目以及颜色数目。
第二行包含 N 个整数, 1, x2..., xn, x表示从位置 1 到位置 N 的珠子的颜色,1 ≤ xi ≤ c。
第三行包含一个整数 Q,表示命令数目。
接下来的 Q 行每行一条命令,如上文所述。
输出文件
对于每一个 C 和 CS 命令,应输出一个整数代表相应的答案。
输入样例
5 3
1 2 3 2 1
4
C
R 2
P 5 5 2
CS 4 1
输出样例
4
1
评分方法
本题没有部分分,你的程序的输出只有和标准答案完全一致才能获得满分,否则不得分。
数据规模和约定
对于 60%的数据,N ≤ 1 000,Q ≤ 1 000;
对于 100%的数据,N ≤ 500 000,Q ≤ 500 000,c ≤ 1 000。

这道题就是一个很裸的线段树。
对于环，有两种处理方式：加倍或者单独处理衔接处。

开始用的加倍的方法，发现有很多问题。
 1) 询问的时候搞忘弄懒标记了。
 2) 数组下标过小。
 3) paint模块弄错。

然后就改成后一种方法，如程序：

/****************************\
 * @prob: NOI2007 necklace  *
 * @auth: Wang Junji        *
 * @stat: Accepted.         *
 * @date: May. 29th, 2012   *
 * @memo: 线段树             *
\****************************/
#include <cstdio>
#include <algorithm>

const int maxN = 1000010; //数组下标要够。
int col[maxN], n, C, T;

class SegTree
{
private:
    struct Node {int L, R, col, cnt, colL, colR;} tr[maxN];
    int lc[maxN], rc[maxN], tot, st, dir;
    int pos(int x) {return (st + dir * (x - 1) + n - 1) % n + 1;}
    void passdown(int p)
    {
        tr[lc[p]].col = tr[rc[p]].col
            = tr[lc[p]].colL = tr[lc[p]].colR
            = tr[rc[p]].colL = tr[rc[p]].colR = tr[p].col;
        tr[lc[p]].cnt = tr[rc[p]].cnt = 1;
        return;
    }
    void update(Node &ths, Node &lc, Node &rc)
    {
        ths.colL = lc.colL; ths.colR = rc.colR;
        if (lc.col == rc.col) ths.col = lc.col; else ths.col = -1;
        ths.cnt = lc.cnt + rc.cnt - (lc.colR == rc.colL);
        return;
    }
    void build(int L, int R)
    {
        int p = ++tot; tr[p].L = L, tr[p].R = R;
        if (L == R)
        {
            tr[p].colL = tr[p].colR = tr[p].col = col[L];
            tr[p].cnt = 1; return;
        }
        int Mid = (L + R) >> 1;
        lc[p] = tot + 1; build(L, Mid);
        rc[p] = tot + 1; build(Mid + 1, R);
        update(tr[p], tr[lc[p]], tr[rc[p]]); return;
    }
    int color(int p, int x)
    {
        if (tr[p].L <= x && tr[p].R >= x && tr[p].col > -1) return tr[p].col;
        int Mid = (tr[p].L + tr[p].R) >> 1;
        return color((x <= Mid) ? lc[p] : rc[p], x);
    }
    void chg(int p, int x, int c)
    {
        if (tr[p].L == tr[p].R && tr[p].L == x)
        {tr[p].col = tr[p].colL = tr[p].colR = c, tr[p].cnt = 1; return;}
        if (tr[p].col > -1) passdown(p), tr[p].col = -1; //
        int Mid = (tr[p].L + tr[p].R) >> 1;
        chg((x <= Mid) ? lc[p] : rc[p], x, c);
        update(tr[p], tr[lc[p]], tr[rc[p]]); return;
    }
    void paint(int p, int L, int R, int c)
    {
        if (L <= tr[p].L && R >= tr[p].R)
        {tr[p].col = tr[p].colL = tr[p].colR = c, tr[p].cnt = 1; return;}
        int Mid = (tr[p].L + tr[p].R) >> 1;
        if (tr[p].col > -1) passdown(p), tr[p].col = -1;
        if (L <= Mid) paint(lc[p], L, R, c);
        if (Mid < R) paint(rc[p], L, R, c);
        update(tr[p], tr[lc[p]], tr[rc[p]]); return;
    }
    Node query(int p, int L, int R)
    {
        if (L <= tr[p].L && R >= tr[p].R) return tr[p];
        if (tr[p].col > -1) passdown(p); //询问时标记需要向下传。
        int Mid = (tr[p].L + tr[p].R) >> 1;
        if (R <= Mid) return query(lc[p], L, R);
        if (Mid < L) return query(rc[p], L, R);
        Node _lc = query(lc[p], L, R), _rc = query(rc[p], L, R), ans;
        update(ans, _lc, _rc); return ans;
    }
public:
    SegTree(): tot(0), st(1), dir(1) {}
    void build() {build(1, n); return;}
    void Rot(int x) {st = (st - x * dir + n - 1) % n + 1; return;}
    void Flip() {dir = -dir; return;}
    void swap(int i, int j)
    {
        if (i == j) return; i = pos(i), j = pos(j);
        int ci = color(1, i), cj = color(1, j); if (ci == cj) return;
        chg(1, i, cj), chg(1, j, ci);
        return;
    }
    void paint(int L, int R, int c)
    {
        L = pos(L), R = pos(R); if (dir < 0) std::swap(L, R);
        if (L <= R) paint(1, L, R, c);
        else paint(1, L, n, c), paint(1, 1, R, c);
        return;
    }
    int query()
    {return std::max(1, query(1, 1, n).cnt - (tr[1].colL == tr[1].colR));}
    int query(int L, int R)
    {
        L = pos(L), R = pos(R); if (dir < 0) std::swap(L, R);
        if (L <= R) return query(1, L, R).cnt;
        else return std::max(1, query(1, L, n).cnt
            + query(1, 1, R).cnt - (tr[1].colL == tr[1].colR));
        //衔接处（即1和n）颜色相等要减去1，但至少要保证有一种颜色
        //（即整个询问区域有且只有一种颜色，可能会弄错成0）。
    }
} Tr;

int main()
{
    freopen("necklace.in", "r", stdin);
    freopen("necklace.out", "w", stdout);
    scanf("%d%d", &n, &C);
    for (int i = 1; i < n + 1; ++i) scanf("%d", col + i);
    Tr.build(); scanf("%d", &T);
    for (int i, j, x; T--;) switch (scanf("\n"), getchar())
    {
    case 'R': scanf("%d", &x); Tr.Rot(x); break;
    case 'F': Tr.Flip(); break;
    case 'S': scanf("%d%d", &i, &j); Tr.swap(i, j); break;
    case 'P':
        scanf("%d%d%d", &i, &j, &x); Tr.paint(i, j, x); break;
    case 'C':
        if (getchar() == 'S')
        {
            scanf("%d%d", &i, &j);
            printf("%d\n", Tr.query(i, j));
        }
        else printf("%d\n", Tr.query());
        break;
    }
    return 0;
}