hdu2647解题报告

题意：有个工厂的老板给工人发奖金，每人基础都是888，工人们有自己的想法，如：a 工人想要比 b 工人的奖金高，老板想要使花的钱最少 那么就可以 给b 888，给a 889 ，但是如果在此基础上，b也想比a高，那么就不能让他们满意，输出 -1；

分析，根据题意可以得出一个拓扑的关系，比如 一组数据：

4 4

1 2

1 3

2 4

3 4

那么有如图关系：(位于上层的要求比下层的高)

 由图可以知道，我们需要给1号890，2、3号889,4号888元，但是我们在拓扑排序的时候总是从入度为0的点 (从图中也就是1号) 开始，如果这样那么我们怎么知道 入度为 0 的点是在第几层呢？那么同样也不好计算总共的奖金数量。

在这里我用的是反向建边，那么建立之后 对于上案例如图：

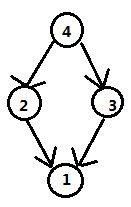如此的时候，我们在拓扑排序的时候第一次找到的点就是没有要求的工人，那么奖励就直接加888，再考虑这一层之后让基本奖励 + 1 ，再拓扑排序便可以了

上马：

// 31MS 476K 
#include<stdio.h>
#include<string.h>

#define MAX 10005

struct node
{
	int to,next;
}edge[MAX*2];
int head[MAX];

void add(int a,int b,int tol)
{
	edge[tol].to=b;
	edge[tol].next=head[a];
	head[a]=tol;
}

int N,M;
int indegree[MAX];
int temp[MAX];//记录临时入度为0点，也就是分析中的在同一层次同一要求奖金额的工人

int topu()
{
	int rw=888;//初始奖励
	int ans=0;//最后奖励总和
	int tol;
	for(int i = 0;i < N;i += tol)
	{
		tol=0;//入度为0的点数
		int j;
		for(j = 1;j <= N; j ++)
			if(indegree[j] == 0)
			{
				temp[tol++]=j;
				indegree[j]=-1;
			}
		if(tol==0) return -1;//没有找到就是形成了环，达不到要求
		ans += rw*tol; rw ++; //这一次入度为0的点数 *  此层的要求奖励额 
		for(j=0;j<tol;j++)//可达边的删除
		{
			for(int k = head[temp[j]];k != -1;k  = edge[k].next)
			{
				int v=edge[k].to;
				indegree[v]--;
			}
		}
	}
	return  ans;
}

int main()
{
	while(~scanf("%d%d",&N,&M))
	{
		int a,b;
		memset(head,-1,sizeof(head));
		memset(indegree,0,sizeof(indegree));
		for(int i = 0 ; i < M ; i ++)
		{
			scanf("%d%d",&a,&b);
			add(b,a,i);//邻接表加边
			indegree[a]++;
		}
		printf("%d\n",topu());
	}
	return 0;
}