【線段樹】Mayor's posters
Description
The citizens of Bytetown, AB, could not stand that the candidates in the mayoral election
campaign have been placing their electoral posters at all places at their whim. The city
council has finally decided to build an electoral wall for placing the posters and introduce
the following rules:
Every candidate can place exactly one poster on the wall.
All posters are of the same height equal to the height of the wall;
the width of a poster can be any integer number of bytes (byte is the unit of length in
Bytetown).
The wall is divided into segments and the width of each segment is one byte.
Each poster must completely cover a contiguous number of wall segments.
They have built a wall 10000000 bytes long (such that there is enough place for all candidates).
When the electoral campaign was restarted, the candidates were placing their posters on the
wall and their posters differed widely in width. Moreover, the candidates started placing their
posters on wall segments already occupied by other posters. Everyone in Bytetown was curious
whose posters will be visible (entirely or in part) on the last day before elections.
Your task is to find the number of visible posters when all the posters are placed given the
information about posters' size, their place and order of placement on the electoral wall.
Input
The first line of input contains a number c giving the number of cases that follow. The first
line of data for a single case contains number 1 <= n <= 10000. The subsequent n lines describe
the posters in the order in which they were placed. The i-th line among the n lines contains
two integer numbers li and ri which are the number of the wall segment occupied by the left
end and the right end of the i-th poster, respectively. We know that for each 1 <= i <= n,
1 <= li <= ri <= 10000000. After the i-th poster is placed, it entirely covers all wall
segments numbered li, li+1 ,... , ri.
Output
For each input data set print the number of visible posters after all the posters are placed.
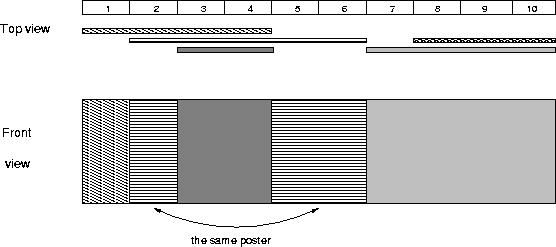
The picture below illustrates the case of the sample input.
Sample Input 1 5 1 4 2 6 8 10 3 4 7 10 Sample Output 4這個題做了很久,還是看了別人的解題報告才做出來的。
思路很簡單,區間離散化+線段樹。
樸素方法(O(m^2)):枚舉牆上的每一個位置,從最後一張海報倒回去找看最先被哪張海報覆蓋,最後統計顏色,但看一看數據,0..10000000,無疑是一個天文數字!
於是需要優化。
優化1:通過觀察可以發現,對於如下幾個區間:[1, 10], [2, 11], [3, 23],中間的很大一部分(如[3, 9]和[11, 23]),這些地方是被白白浪費掉了的!
於是可以將這些部分舍掉,即將這幾個區間分別變成[1, 4], [2, 5], [3, 6],這樣既沒有改變區間之間的覆蓋關係,又大大減少枚舉量。
優化2:使用線段樹。
區間統計問題大都可以通過線段樹進行優化,當整個區間為單色時,就不需要對其子區間進行遍曆。
Accode:
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <bitset>
using std::bitset;
const char fi[] = "poj2528.in";
const char fo[] = "poj2528.out";
const int maxN = 10010;
const int MAX = 0x3fffff00;
const int MIN = -MAX;
struct SegTree {int L, R, lc, rc, color; };
struct Seg {int pos, Ind, sym; };
SegTree tree[maxN << 3];
Seg seg[maxN << 1];
bitset <maxN> marked;
int L[maxN], R[maxN];
int n, N, tot, cnt;
void init_file()
{
freopen(fi, "r", stdin);
freopen(fo, "w", stdout);
}
int cmp(const void *a, const void *b)
{return ((Seg *)a) -> pos - ((Seg *)b) -> pos; }
void Build(int L, int R)
{
int Now = ++tot;
tree[Now].L = L;
tree[Now].R = R;
tree[Now].lc = 0;
tree[Now].rc = 0;
tree[Now].color = 0;
//所有標記清零。
if (L + 1 < R)
{
int Mid = (L + R) >> 1;
tree[Now].lc = tot + 1;
Build(L, Mid);
tree[Now].rc = tot + 1;
Build(Mid, R);
}
//遞歸建樹。
}
void insert(int Now, int i)
{
if (L[i] > tree[Now].R || R[i] < tree[Now].L)
return;
//若當前被插入的線段與這個區間無
//交集,則不需要遍曆。
if (L[i] <= tree[Now].L && R[i] >= tree[Now].R)
{tree[Now].color = i; return; }
//若該區間被完全覆蓋,直接染色並退出。
if (tree[Now].color > -1)
{
tree[tree[Now].lc].color =
tree[tree[Now].rc].color =
tree[Now].color;
tree[Now].color = -1;
} //若開始時該區間為單色或無色,
//則標記向下傳,並把該區間標記為多色。
int Mid = (tree[Now].L + tree[Now].R) >> 1;
if (L[i] < Mid) insert(tree[Now].lc, i);
if (Mid < R[i]) insert(tree[Now].rc, i);
//依次對它的左右子區間進行統計。
}
void count(int Now)
{
if (tree[Now].color == 0) return;
//如果該區間沒有顏色,
//那麼其子區間不需要被遍曆。
if (tree[Now].color > 0)
{
if (!marked.test(tree[Now].color))
{marked.set(tree[Now].color); ++cnt; }
return;
} //若該區間為單色,統計該顏色後
//就不需要對其子區間進行統計了。
if (tree[Now].lc) count(tree[Now].lc);
if (tree[Now].rc) count(tree[Now].rc);
//若該區間為多色,那麼需要對各個子區間
//分別進行統計。
}
void work()
{
scanf("%d", &N);
for (; N; --N)
{
scanf("%d", &n);
int x, y;
tot = 0;
for (int i = 1; i < n + 1; ++i)
{
scanf("%d%d", &x, &y);
seg[++tot].pos = x;
seg[tot].sym = 1;
seg[tot].Ind = i;
seg[++tot].pos = y + 1;
seg[tot].sym = -1;
seg[tot].Ind = i;
}
qsort(seg + 1, n << 1,
sizeof(seg[0]), cmp);
//按照座標從左到右排序,方便壓縮。
int Last = 1;
if (seg[1].sym == 1)
L[seg[1].Ind] = 1;
if (seg[1].sym == -1)
R[seg[1].Ind] = 1;
for (int i = 2; i < (n << 1) + 1; ++i)
{
if (seg[i].pos == seg[i - 1].pos)
{
if (seg[i].sym == 1)
L[seg[i].Ind] = Last;
if (seg[i].sym == -1)
R[seg[i].Ind] = Last;
}
if (seg[i].pos > seg[i - 1].pos)
//壓縮區間,“毀掉”不需要用掉的空間。
{
if (seg[i].sym == 1)
L[seg[i].Ind] = ++Last;
if (seg[i].sym == -1)
R[seg[i].Ind] = ++Last;
}
}
tot = 0;
Build(1, Last);
//建立線段樹。
for (int i = 1; i < n + 1; ++i)
insert(1, i);
marked.reset();
cnt = 0;
count(1);
printf("%d\n", cnt);
}
}
int main()
{
init_file();
work();
exit(0);
}