06-VTK基本数据结构(2)
6.3 单元类型
数据集由一个或多个单元组成,图6.6和6.7列出了VTK支持的线性和非线性类型的单元。一系列有序的点按指定类型连接所定义的结构就是单元(Cell),单元是可视化系统的基础。这些点的连接顺序通常也称为顶点列表(Connectivity List);所指定的类型定义了单元的拓扑结构,而点的坐标定义了单元的几何结构。
比如,图6.8是类型为六面体(Hexahedron)的单元,顶点列表(由点的索引号表示,即8-10-1-6-21-22-5-7,每个点通过索引号可在顶点列表中检索到该点的实际坐标值)定义了六面体单元的拓扑结构,从图中可以看出,索引为8和10的点连接就构成了六面体十二条边中的其中一条,而8-10-1-6这四个点连接就构成了六面体其中的一个面。在这个示例中,可以看出单元是由单元的类型(如六面体)和构成单元的顶点列表两部分构成。
通常我们用数学符号Ci来表示单元,换言之,单元就是一个有顺序的点集:Ci = {p1, p2,…, pn},其中pi∈P,P就是该有序的点集。单元的类型决定了点集里点的顺序,或者说单元的拓扑;而定义单元的点的个数就是该单元的大小(Size)。
单元的拓扑维度除了三维(图6.8)之外,还可以是零维、一维、二维等,如零维的顶点(Vertex)、一维的线(Line)以及二维的三角形(Triangle)。单元可以是基本类型或者基本类型的组合,基本类型是指不可再分的单元,组合类型是由基本类型组合而成。比如,三角形条带(Triangle Strip)是由多个三角形所组成,即三角形条带可以分解成多个三角形,而三角形是二维的基本单元类型。所以,对于单元的类型而言,理论上由不同类型的单元可以组合成无数种,VTK应用程序需要用到哪些类型的单元应该根据具体的要求。总的来说,VTK里的单元类型分为线性、非线性(图6.6和图6.7)和其他类型,接下来的内容主要介绍VTK里定义的单元类型。
6.3.1 线性单元
单元类型的线性与非线性的划分主要是以插值函数为依据的,对于线性单元,采用的是线性或者常量插值函数。另外,单元里的任意一条边都是由两个点连接定义的。VTK里单元的类型定义在vtkCellType.h文件里,线性的单元类型有:
Vertex:VTK_VERTEX,顶点,由一个点定义,是零维的基本类型。
Polyvertex:VTK_POLY_VERTEX,多顶点,多个顶点组合而成,是零维的组合单元,其定义不受顶点顺序的限制。
Line:VTK_LINE,直线,一维的基本类型,由两个点定义,方向是从第一个点指向第二个点。
Polyline:VTK_POLY_LINE,折线,由一条或多条直线组合而成,属于一维的类型。由n+1个有序的点连接定义的,n表示折线的线段条数,每两个点(i, i+1)定义一条线段。
Triangle:VTK_TRIANGLE,三角形,二维的基本类型,由三个点按逆时针的方向连接定义的,点的连接方向和表面法向量符合右手法则,即除大拇指外的手指沿着点的方向弯曲,大拇指所指向的方向就是表面法向量。
TriangleStrip:VTK_TRIANGLE_STRIP,三角形条带,由一个或多个三角形组合而成,二维的类型。由n+2个有序的点连接定义的,n表示三角形条带里三角形的个数,定义三角形条带的点不需要共面。定义每个三角形的顶点顺序为(i, i+1, i+2),0≦i≦n。
Quadrilateral:VTK_QUAD,四边形,二维的基本类型,由共面的四个点按逆时针的方向连接定义的。四边形要求是凸多边形,且它的边不能相交。利用右手法则可以得到该四边形的表面法向量。
Pixel:VTK_PIXEL,二维的基本类型,由共面的四个点按一定的顺序连接定义的。该类型的单元与四边形的区别在拓扑结构上,Pixel类型要求相邻的两条边必须垂直,而且相对的两条边要与坐标轴平行,因此Pixel的表面法向量也与其中的一条坐标轴平行。
图6.6 VTK里定义的线性的Cell类型
图6.7VTK里定义的非线性的Cell类型
图6.8 六面体Cell
定义Pixel的四个顶点的顺序与四边形的不同,如图6.6-h所示,Pixel顶点的计数是先沿着X轴的方向,然后是Y轴,最后是Z轴方向。Pixel是四边形类型的特殊形式,但要注意这里的Pixel是一种单元类型,与图像像素(Pixel)的概念是不同的。Pixel具体表达什么意思,需要根据上下文来作判断。
Polygon:VTK_POLYGON,多边形,二维的基本类型,由共面的三个或以上的点按逆时针方向的顺序连接定义的。多边形表面法向量的方向通过右手法则确定。
多边形可以是凹多边形,也可以是凸多边形,但是不能含有内部循环或者出现相交的边。多边形有n条边,n就是组成多边形的点的个数。
Tetrahedron:VTK_TETRA,四面体,三维的基本类型,由不共面的四个点两两连接定义的。如图6.6-j所示,四面体有六条边和四个面。
Hexahedron:VTK_HEXAHEDRON,六面体,三维的基本类型,包含六个四边形表面、12条边和8个顶点。其中8个顶点的连接顺序如图6.6-k所示,六面体要求必须是凸的。
Voxel:VTK_VOXEL,三维的基本类型,与六面体的拓扑一样,但几何上有所区别。Voxel要求相邻的两个面必须垂直,点的连接顺序如图6.6-l所示。Voxel是六面体的特殊形式。与Pixel类似,Voxel与三维图像体素(Voxel)的概念是不同的。
Wedge:VTK_WEDGE,楔形,三维的基本类型,由三个四边形面、两个三角形面、九条边和六个顶点构成。六个点的连接顺序如图6.6-m所示。要求面和边不能与其他的相交,且楔形必须是凸的。
Pyramid:VTK_PYRAMID,角椎体,三维的基本类型,由一个四边形面、四个三角形面、八条边和五个顶点构成。构成角椎体的点的连接顺序如图6.6-n所示。定义四边形的四个点要求是共面的,且四个点构成的四边形必须是凸的,第五个点与其他四个点不在一个面上。
PentagonalPrism:VTK_PENTAGONAL_PRISM,五棱柱,三维的基本类型,由五个四边形面、两个五边形面、十五条边和十个顶点构成。点的连接顺序如图6.6-o所示。五棱柱的面和边不能与其他的相交,且五棱柱必须是凸的。
HexagonalPrism:VTK_HEXAGONAL_PRISM,六角柱,三维的基本类型,由六个四边形面、两个六边形面、十八条边和十二个顶点构成。点的连接顺序如图6.6-p所示。六角柱的面和边不能与其他的相交,且六角柱必须是凸的。
6.3.2 非线性单元
数值分析领域里,为了更准确、精确地表达数据,采用非线性单元作为数据的基本表达结构。线性单元和非线性单元的不同点是在绘制和数据处理方法方面,线性单元可以很容易的转换成线性图元被图形库处理,而非线性单元不被图形库直接支持,因此非线性单元必须先转换成线性单元以后,才能被图形库所支持。
VTK除了提供一套复杂的非线性单元接口框架,另一种做法就是在非线性单元的每一条曲线增加一个关键点(如图6.7所示),或者增加一个曲面来近似模拟非线性单元。可视化系统在处理非线性单元时,一种比较流行的做法就是细化(Tessellation)非线性单元,充分利用线性单元的可视化算法。但是细化的过程必须谨慎处理,否则会导致过分细分,造成过多的线性单元。
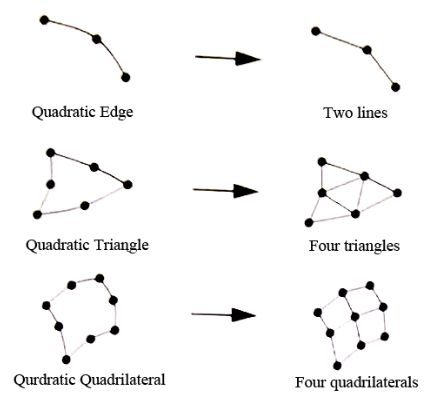
VTK在细化非线性单元时,采取如图6.9所示固定的细化方式。一条二次曲线通过加入一个关键点,细化成两点直线;一个二次三角形分别在三条边上增加三个点,细化成四个线性三角形;一个二次四边形分别在四条边上增加四个点,细化成四个线性四边形。也就是:在VTK里,二次曲线(QuadraticEdge)是一维的基本单元,由三个点定义,前两个点定义了曲线的起点和终点,第三个点位于起点与终点的中间位置(参考图6.7-a);二次三角形(QuadraticTriangle)是二维的基本单元,由六个点定义,前三个点位于三角形的顶点,后三个点位于每条曲线的中点位置;二次四边形(QuadraticQuadrilateral)也是二维的基本单元,由八点定义,前两个点位于四边形的四个顶点处,后四个点位于每条边的中点位置。其他类型的非线性单元可参考图6.7。
图6.9VTK细化非线性单元示意图