无源无汇带上下界的可行流
1.无源汇最大流
2.有源汇最大流
3.有源汇最小流
1.无源汇最大流问题sgu194
题意:
给n个点,及m根pipe,每根pipe用来流躺液体的,单向的,每时每刻每根pipe流进来的物质要等于流出去的物质,要使得m条pipe组成一个循环体,里面流躺物质。
并且满足每根pipe一定的流量限制,范围为[Li,Ri].即要满足每时刻流进来的不能超过Ri(最大流问题),同时最小不能低于Li。
例如:
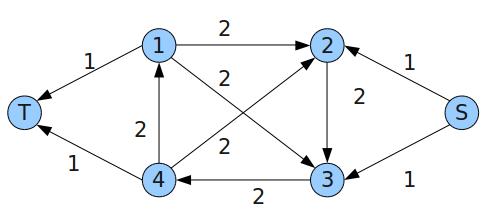
46(4个点,6个pipe)
12 1 3 (1->2上界为3,下界为1)
23 1 3
3 4 1 3
4 1 1 3
1 3 1 3
4 2 1 3
可行流:
再如:所有pipe的上界为2下界为1的话,就不能得到一种可行流。
题解:
上界用ci表示,下界用bi表示。
下界是必须流满的,那么对于每一条边,去掉下界后,其自由流为ci– bi。
主要思想:每一个点流进来的流=流出去的流
对于每一个点i,令
Mi= sum(i点所有流进来的下界流)– sum(i点所有流出去的下界流)
如果Mi大于0,代表此点必须还要流出去Mi的自由流,那么我们从源点连一条Mi的边到该点。
如果Mi小于0,代表此点必须还要流进来Mi的自由流,那么我们从该点连一条Mi的边到汇点。
如果求S->T的最大流,看是否满流(S的相邻边都流满)。
满流则有解,否则无解。
2.有源汇最大流
zoj3229
题意:经过构图之后得到这样的问题,源点s,汇点t,有些边有上下界[Li,Ri].求s->t的最大流。
题解:
满足所有下界的情况下,判断是否存在可行流,方法可以转化成上面无源汇上下界判断方法。
只要连一条T→ S的边,流量为无穷,没有下界,那么原图就得到一个无源汇的循环流图。接下来的事情一样:原图中的边的流量设成自由流量ci– bi。新建源点SS汇点TT,求Mi,连边。然后求SS→ TT最大流,判是否满流。
判定有解之后然后求最大流,信息都在上面求得的残留网络里面。满足所有下界时,从s→ t的流量为多少?后悔边s→ t的边权!然后在残留网络中s→ t可能还有些自由流没有流满,再做一次s→ t的最大流,所得到的最大流就是原问题的最大流(内含两部分:残留的自由流所得到的流+后悔边s→ t)。
3.有源汇最小流
题意:经过构图之后得到这样的问题,源点s,汇点t,有些边有上下界[Li,Ri].求s->t的最小流。
题解:
同样先转换为无源汇网络流问题,添加t→ s边权为无穷。那么最小流不就是在满足所有下界的情况的流么。即上面提到的,求得SS→ TT的最大流之后,其后悔边s→ t的边权即为最小流。但是wa了,下面看一个wa的例子:
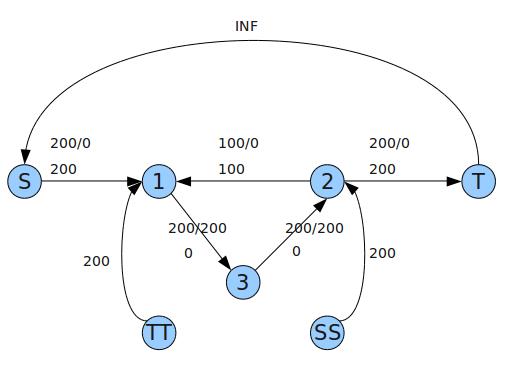
最后求得SS→ TT的最大流之后,得到后悔边s→ t的边权为200,实际上该网络最小流只要100:
s→ 1:100
1→ 3:200
3→ 2:200
2→ 1:100
2→ t:100
问题出在原图中存在环,循环流,而我们没有利用,导致流增大了。
解决方法:先不加t→ s边权为无穷的边,求SS→ TT的最大流,如果还没有流满则再加t→ s边权为无穷的边,再求一次最大流得到后悔边s→ t就是原问题的最小流了。
zoj_3229_AC_code:
/*求有源汇的最大流问题*/
memset(in,0,sizeof (in)); /*初始化出度,入度,用于求Mi*/
memset(out,0,sizeof (out));
M= n+m+2; /*初始化网络,设置源点汇点*/
s= 0;
t= M-1;
cnt= -1;
memset(mat,0,sizeof (mat));
for(int i=1;i<=n;i++) { /*添加自由流*/
for(int j=1;j<=C[i];j++) {
addEdge(i,n+T[i][j],R[i][j]-L[i][j],0);
in[n+T[i][j]]+= L[i][j];
out[i]+= L[i][j];
}
}
for(int i=1;i<=n;i++) {
addEdge(s,i,D[i],0);
}
for(int i=1;i<=m;i++) {
addEdge(n+i,t,INF - G[i],0);
in[t]+= G[i];
out[n+i]+= G[i];
}
addEdge(t,s,INF,0); /*添加一条t→ s的边,权值为INF*/
M+= 2; s = M-1; t = s-1; /*添加SS,TT*/
sum= 0;/*满流变量*/
for(int i=0;i<M;i++) { /*根据Mi连边*/
if(in[i] > out[i]) {
addEdge(s,i,in[i] - out[i],0);
sum+= in[i] - out[i];
}else {
addEdge(i,t,out[i] - in[i],0);
}
}
intmaxflow = dinic (); /*求SS→ Tt的最大流*/
if(sum != maxflow) { /*不满流则输出-1*/
printf("-1\n\n");
continue;
}
mat[s]= 0; /*删除SS,TT*/
mat[t]= 0;
M= n+m+2;
s= 0;
t= M-1;
maxflow= dinic (); /*求s→ t的最大流,为原问题的解*/
printf("%d\n",maxflow);
intmm = -1;
for(int i=1;i<=n;i++) {
for(int j=1;j<=C[i];j++) {
mm++;
printf("%d\n",R[i][j] - edge[2*mm].cap);
}
}
printf("\n");
sgu_176_AC_code:
/*有源汇的最小流*/
memset(in,0,sizeof (in)); /*初始化出度,入度,用于求Mi*/
memset(out,0,sizeof (out));
M= n+1; /*初始化网络,设置源点汇点*/
s= 1;
t= M-1;
cnt= -1;
memset(mat,0,sizeof (mat));
for(int i=1;i<=m;i++) { /*添加自由流*/
if(c[i] == 1) {
in[v[i]] += z[i];
out[u[i]] += z[i];
addEdge (u[i],v[i],0,0);
}else {
addEdge (u[i],v[i],z[i],0);
}
}
M+= 2; s = M-1; t = s-1; /*添加SS,TT*/
intsum = 0; /*满流变量*/
for(int i=1;i<=n;i++) { /*根据Mi连边*/
if(in[i] > out[i]) {
addEdge(s,i,in[i] - out[i],0);
sum+= in[i] - out[i];
}else {
addEdge(i,t,out[i] - in[i],0);
}
}
intmaxflow = dinic (); /*求SS→ TT的最大流,先流完途中的循环流*/
intmmm = cnt; /*记录新加的t→ s无穷边的编号,以便求后悔边的权值*/
addEdge(n,1,INF,0); /*添加一条t→ s的边,权值为INF*/
maxflow+= dinic (); /*求SS→ TT的最大流*/
if(sum != maxflow) { /*不满流则输出-1*/
printf("Impossible\n");
return0;
}
printf("%d\n",edge[mmm+2].cap); /*最小流为后悔边:s→ t的权值*/
intmm = -1;
boolfirst = 1;
for(int i=1;i<=m;i++) {
if (first) {
first = 0;
} else {
printf (" ");
}
if(c[i]) {
printf ("%d",z[i]);
}else {
printf ("%d",z[i] - edge [2*i-2].cap);
}
}
printf("\n");