如何测试搜索引擎的索引量大小
背景知识:
搜索引擎的质量指标一般包括相关性(Relevance)、时效性(Freshness)、全面性(Comprehensiveness)和可用(Usability)等四个方面,今天我们要谈的索引量就属于完整性指标的范畴。 首先需要注意的是,对于搜索引擎,网页的索引量和抓取量是不同的概念。搜索引擎的网页抓取数量一般都要远大于索引量,因为抓取的网页中包括很多内容重复或者作弊等质量不高的网页。搜索引擎需要根据算法从抓取的网页当中取其精华,去其糟粕,挑选出有价值的网页进行索引。因此,对用户而言,搜索引擎的索引量大小才更有意义。 其次,无限制增大索引量并不一定能保证搜索质量的提升。一方面,在全面性指标中,除索引量外,还需要考虑到收录网页的质量和不同类型网页的分布。另一方面,搜索引擎的质量指标体系要保证四方面的均衡发展,不是依靠单个指标的突破就可以改善的。目前包括雅虎中国在内的主流中文搜索引擎的网页索引量都在20亿量级,基本上可以满足用户的日常查询需求。 然而,由于从外部无法直接测算出搜索引擎网页索引量的绝对值大小,很多搜索引擎服务商喜欢对外夸大自己的收录网页数,作为市场噱头。从1998年开始,Krishna Bharat和Andrei Broder就开始研究,如何通过第三方来客观比较不同搜索引擎索引量的大小。8年后,在今年5月份的WWW2006大会上,来自以色列的Ziv Bar-Yossef和Maxim Gurevich由于这方面的出色研究成果夺得了大会唯一的最佳论文奖。他们的研究算出了主流英文搜索引擎的索引量相对大小:雅虎是Google的1.28倍,Google是MSN的1.36倍。他们是如何算出这些数字的呢?下面我们将为搜索引擎爱好者介绍这个算法,以及探讨在中文搜索引擎上是如何应用的。 概述 搜索引擎的索引量或称覆盖率对搜索结果的相关性、时效性和找到率都具有深远的影响。出于市场运作的考虑,各大互联网搜索引擎不时对外公布自己索引的文档数量,然而这些数据往往不同程度地被加入了一些水份,可信度上有一个问号。因此,如何通过搜索引擎的公共接口,也就是通常所说的搜索框,比较客观、准确地测试它的索引量就成为了一个令人关注的问题。
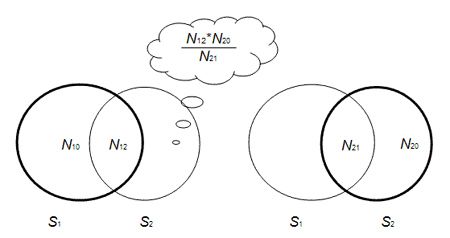
每一个搜索引擎的索引都覆盖了互联网上全部文档的一个子集。如果我们把测试作为对这个集合的采样,那么问题的关键就在于如何实现一个近似的等概率随机采样(uniform search engine url sampler),参见图1。具体地说,假定一个搜索引擎S总共索引了|D|个文档,那么我们希望采样得到某一个具体文档的概率是1/|D|。 一旦实现了通过搜索框对索引的等概率随机采样,我们就可以在统计意义上比较有把握地估计搜索引擎索引量的相对大小。如下图:
比较搜索引擎索引的相对大小 我们先对引擎S1随机采样N1个url。然后,通过url查询获知引擎S2索引了其中的N12个url,而没有索引另外N10个。换句话说,N1 = N10+N12 。同样地,如果我们对引擎S2随机采样N2个url,发现其中N21被S1收录而N20没有收录,N2=N20+N21。那么我们可以估计S1与S2的相对大小为: |D1|/|D2| ≌(N12+N10) / (N12+N12N20/N21) =(N1N21)/(N2N12) =N21/N12 (如果N1══N2) 搜索引擎索引的等概率随机采样:Ziv Bar-Yossef 等人的方法介绍 对于搜索引擎等概率随机采样的研究已经有了相当长的历史,具体的背景文献我们不准备在这里一一探讨。我们希望通过对Bar-Yossef等人最近工作的介绍,把一种比较客观、科学的测试方法推介给读者。我们也会探讨他们的方法对于中文索引的局限性和一些解决方案。
一个简化的搜索引擎索引:
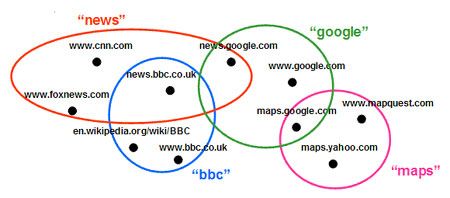
图3给出了一个简化了的搜索引擎索引示例:
假定关键字“news”将返回4个结果:www.cnn.com、news.google.com、www.foxnews.com和news.bbc.co.uk。 首先我们给出一组定义 关键字搜索结果集合:results(q) = { 搜索关键字 q所返回的全部结果文档之集合} 文档关键字集合:queries(x) = { 所有能返回文档x的搜索关键字之集合} 搜索关键字池P:一组理论上能够覆盖所有文档的搜索关键字集合 例如图3中P = {news, bbc, maps, google} 关键字搜索结果量:card(q) = |results(q)|,搜索关键字 q所返回的全部结果文档之数量。
例如图3中 card(“news”) = 4,card(“bbc”) = 3 文档匹配度: deg(x) = |queries(x)| ,全体能够匹配文档x的搜索关键字数量 例如图3中deg(www.cnn.com) = 1,deg(news.bbc.co.uk) = 2 当我们通过搜索框对搜索引擎的索引进行采样,所获得的结果实际上偏向于匹配度高的文档。对于图3所示的搜索引擎,如果我们从搜索关键字池P = {news, bbc, maps, google}中任意选取一个关键字,然后在所得搜索结果中任意选取一个文档,那么选到某一个具体文档的概率与它的匹配度成正比,例如,p(news.bbc.co.uk) = 2/13 ,p(www.cnn.com) = 1/13 因此,通过关键字对搜索引擎的索引进行采样,实际上是对文档匹配度概率分布在作随机抽样。具体地说,如果相对于一个给定的搜索关键字池P,该索引的全部文档匹配度的总和为deg(D) = ∑x∈D deg(x),那么通过搜索框对引擎采样获取具体一个文档x的概率是deg(x)/ deg(D)。
如何通过对文档匹配度分布的随机抽样而获得我们所期望的等概率随机采样呢?这正是Bar-Yossef 等人工作的主要成果所在:他们采用蒙特卡罗仿真(Monte Carlo Simulation)算法实现了这一点 目标分布π(x) : D上的等概率随机分布, π(x) = 1/|D| 实际采样分布p(x) : D上的文档匹配度随机分布,p(x) = deg(x) / ∑x'∈Ddeg(x') 偏差权值: w(x) = π(x)/p(x) ∝1/deg(x) 采样过程,参见图4:
选定一个搜索关键字池P 随机选取q ∈P 在搜索结果中随机选取一个文档x ∈results(q) 计算该文档对P 的匹配度deg(x) 产生一个0~1的随机数r,如果r ≤ 1/deg(x)保留该文档,否则放弃 重复上述过程直到获得N个有效采样点图4,通过蒙特卡罗仿真(Monte Carlo Simulation)算法实现对索引的等概率随机采样 问题和讨论 上述算法在数学上非常严谨优美,但是在具体的实现过程中仍然有相当多的困难,尤其是对于中文搜索引擎,有一些特殊的问题需要探讨。
搜索关键字池P的选取:
P选择的条件是:
(1)要保证p(x) = 0,即索引中文档不匹配任何一个关键字q ∈ P的概率足够小。如果这个概率太高,测试只能局限于索引的一小部分,测试的结果就失去了意义。
(2)关键字搜索结果量card(q)最好要比较小,这样可以尽可能地避免搜索结果超过搜索引擎允许返回结果的上限。作者提出的方案是通过抓取和分析一个大型的网上文库,例如维基百科全书,选择其中所有的英文单词的集合或者所有K个相连单词的集合作为P。这对于没有分词问题的英文而言是容易实现的,但对于汉语等需要分词的语种,这个方法似乎并不很合适。我们建议直接采用GBK字库中的全部字符,或者采用中文分词标准中所有词汇的集合。
如何计算文档对P的匹配度deg(x)? 文档匹配度deg(x)必须离线计算,通过查询获得是不现实的。对英文文档来说,只要计算文档中覆盖了多少个关键字q ∈P。但是对中文而言,不同引擎包含了不同的搜索逻辑,例如四个汉字以下的搜索通常采取词组搜索,长搜索词有些引擎可能采取与或逻辑。不同引擎对于汉语分词的处理也有较大的差异。在索引文档时,有些引擎可能考虑了繁简汉字的转换。所有这些都会对匹配度产生一定程度的影响。 实际上,匹配度deg(x)的计算并不一定要十分精确,一些近似处理是可以接受的,只要误差不至于太大。我们建议用GBK字库的单个汉字集合作为P,这样可以避免分词的差异。而此时文档的匹配度就是一个文档包含不同GBK字符的个数。 搜索引擎对搜索最大返回结果的限制。 这一点Bar-Yossef 等人的文章中有比较详细的讨论,他们认为这个限制对于测试结果的影响并不太大。 该算法的计算复杂度比较高。 从计算量上考虑,由于deg(x)一般都比较大,因此搜索结果文档被放弃的比例较高,如何进一步改进算法的复杂度是一个值得探讨的问题。
参考文献 * Ziv Bar-Yossef and Maxim Gurevich, Random Sampling from a Search Engine's Index
本文来自CSDN博客,转载请标明出处:http://blog.csdn.net/iptvspace/archive/2008/07/01/2602537.aspx