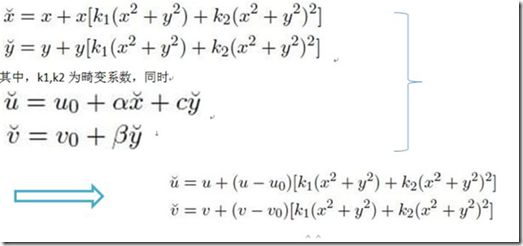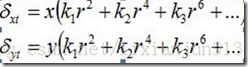单目相机标定原理
一.相机标定主要涉及三个坐标系:图像坐标系、摄像机坐标系和世界坐标系
【图像坐标系】
摄像机采集的图像变换为数字图像后,每副数字图像在计算机内为M x N数组,M行N列的图像中每一个元素(pixel)数值就是图像点的亮度(灰度)。如图,在图像上定义直角坐标系(U,V),每一个像素为单位的图像坐标系坐标,由于(u,v)只能表示像素位于数组中的列数与行数,并没有使用物理单位表示该像素在图像中位置,所以需要再建立以物理单位(mm)表示的图像坐标系,该图像坐标系以图像内某一点O1为原点,X轴和Y轴分别平行于U轴和V轴。
如图中,(u、v)表示以像素为单位的图像坐标系的坐标,(x、y)表示以mm为单位的图像坐标系的坐标。在X、Y坐标系中,原点O1定义在摄像机光轴与图像平面的交点,该点一般位于图像中心。但是由于制造原因,很多情况下会有偏移。若O1在U、V坐标系中坐标为(u0,v0),每一个像素在X轴与Y轴方向上的物理尺寸为dx、dy,则图像任一像素在两个坐标系下有如下关系:
【摄像机坐标系】
如图,Oc点为摄像机光心,Xc轴和Yc轴与图像的X轴与Y轴平行,Zc轴为摄像机光轴,它与图像平面垂直。光轴与图像平面的交点,即为图像坐标系的原点。由点Oc与Xc、Yc、Zc轴组成的直角坐标系称为摄像机坐标系,OOc为摄像机焦距:
由于摄像机可以安放在现实环境中任意位置,所以在环境中任选一个基准坐标系来描述摄像机位置,并用它描述环境中任何物体的位置,该坐标系为世界坐标系。它有Xw、Yw和Zw轴组成,摄像机坐标系与世界坐标系之间的关系可以用旋转矩阵与平移向量t来描述。
总体来说,世界坐标系到图像坐标系的关系可总结如下:
摄像头成像几何关系,其中Oc点称为摄像头(透镜)的光心,Xc轴和Yc轴与图像的x轴和Y轴平行,Zc轴为摄像头的光轴,它与图像平面垂直。光轴与图像平面的交点O1,即为图像坐标系的原点。由点Oc与Xc、Yc、Zc轴组成的坐标系称为摄像头坐标系,Oc O1 的距离为摄像头焦距,用f表示。
图像坐标系是一个二维平面,又称为像平面,实际上就是摄像头的CCD传感器的表面。每个CCD传感器都有一定的尺寸,也有一定的分辨率,这个就确定了毫米与像素点之间的转换关系。举个例子,CCD的尺寸是8mm X 6mm,帧画面的分辨率设置为640X480,那么毫米与像素点之间的转换关系就是80pixel/mm。”设CCD传感器每个像素点的物理大小为dx*dy,相应地,就有dx=dy=1/80。
二. 针孔模型
又称为线性摄像机模型,任何空间点M在图像中的投影位置m,为光心Oc与M的连线OcM与图像平面的交点(各种相似三角形有木有,但是要注意像平面和现在讨论的其实是关于Oc对称的哦,所以计算的时候不要忘记了负号,不然出来的图像就是倒着的啦),这种关系也称为重心摄影或者透视投影。此时有比例关系如下:
将上面的世界坐标到摄像机坐标的转换代入,最后皆可以得到世界坐标系与摄像机坐标系之间的关系啦:
其中,很容易可以知道alph=f/dx,beta=f/dy,分别代表了以X轴与Y轴方向上的像素为单位表示的等效焦距。gamma在较高精度的相机模型中引入,表示图像平面中以像素为单位的坐标轴倾斜程度的量度,gamma=alpha*tan(theta),theta是相机CCD阵列v轴的偏斜角度。
由针孔模型我们可以知道,如果一直摄像机的内外参数,就知道投影矩阵M,这时候对任何空间点就可以求出其对应图像坐标,但是如果已知空间某点的像点m位置(u,v)即使已经知道摄像机内外参数,Xw也不能唯一确定,因为在投影过程中消去了Zc的信息。
在上面的式子中M是3x4不可逆矩阵,当已知M与(u,v)时,由公式得到的三个方程中消去z,只可以得关于Xw,Yw与Zw的两个线性方程,这个方程组即为射线OP的方程,也就是说,投影点为m的所有点均在该射线上,所以,该空间是不能唯一确定的。
三. 相机畸变
摄像头由于光学透镜的特性使得成像存在着径向畸变,可由三个参数k1,k2,k3确定;由于装配方面的误差,传感器与光学镜头之间并非完全平行,因此成像存在切向畸变,可由两个参数p1,p2确定。单个摄像头的定标主要是计算出摄像头的内参(焦距f和成像原点cx,cy、五个畸变参数(一般只需要计算出k1,k2,p1,p2,对于鱼眼镜头等径向畸变特别大的才需要计算k3))以及外参(标定物的世界坐标)。OpenCV中使用的求解焦距和成像原点的算法是基于张正友的方法,而求解畸变参数是基于 Brown 的方法。
1.径向畸变
设(u、v)为理想的图像像素坐标,相对应的, 为真实获得的像素坐标。则(x,y)就为理想的图像物理坐标, 为实际获得的图像物理坐标,可以得到如下的关系式:
我们知道,(u0,v0)在求摄像机内参的时候可以知道,![]() 在圆心提取排序后也可以知道,(u,v)可以通过OpenCV中cvProjectpoints函数求得反投影残差。(x,y)可以通过 和
在圆心提取排序后也可以知道,(u,v)可以通过OpenCV中cvProjectpoints函数求得反投影残差。(x,y)可以通过 和![]() 求出,于是克得到如下公式:
求出,于是克得到如下公式:
设Dk=d,所以可以求出畸变系数k1,k2.
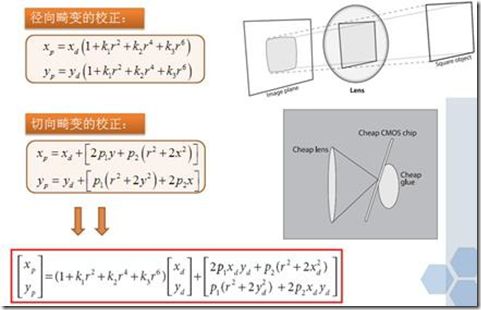
在求得了径向畸变的系数以后,就可以如下得到成像仪某点理想的径向位置
其中,r就是当前点的所在透镜半径,k3只有在精度很高的时候才用得到(可以看到其实是将径向畸变做了一个泰勒展开并忽略高阶误差得到的)
2.切向畸变(由于透镜表面曲率不总是严格共线产生)
主要包括离心畸变和薄棱镜畸变,其中,离心畸变是由摄像机的镜头中各个透镜的光轴不能完全重合造成的。
离心畸变其数学模型可以表示为:
薄棱镜畸变是由镜头设计和制造缺陷等误差造成(比如镜头与摄像机像面之间有很小的倾角,其不仅会引起径向偏差,而且会引起切向误差)其数学模型为:
可以看到,薄棱镜畸变的结果就是之前内参矩阵求解时候的那个gamma啦![]()
综合考虑径向畸变和切向畸变,就需要对小孔成像模型进行修正,理想的图像点归一化坐标为p=(x,y)T,有畸变的图像点的归一化坐标为Pd=(xd,yd)T之间关系为:
特别说明:在opencv中求出了畸变系数和摄像机内参数以后,就可以用cvUndistort2( ImageC1, Show1, &intrinsic_matrix, &distortion_coeffs);来进行图像矫正了 (建议使用Matlab工具箱来矫正,Opencv自己的函数误差不是一般大,而且对角点提取的精度要求超高(虽然用了亚像素级别),⊙﹏⊙b汗,之前自己按照书上来结果发现矫正以后图像扭曲的不行还以为自己的问题查错查了好久,结果直接标定传入参数进行矫正以后各种准确…….)。
附录:cvUndistort2的函数说明