Internet路由之路由表查找算法概述-哈希/LC-Trie树/256-way-mtrie树
Internet路由之路由表查找算法概述-哈希/LC-Trie树/256-way-mtrie树
From:http://blog.csdn.net/dog250/article/details/6596046
说明:本文没有源码分析的内容,然而我认为能理解本质比能看懂源码更有用,因为理解了本质之后,你也许就不用再看源码了,你甚至都可以写源码了。这就是Linux内核和Cisco的网站中包含大量文档的原因。
引:路由是互联网的一个核心概念,广义的讲,它使分组交换网的每个节点彼此独立,通过路由耦合在一起,甚至在电路交换网中,虚电路的建立也依赖路由,路由就是网络中数据通路的指向标。狭义的讲,路由专指IP路由,它支撑着整个IP网络。由于IP是数据报网络,它是不建立连接的,因此IP分组是一跳一跳被转发,通路是通过路由信息 一跳一跳的被打通的,因此路由直接关系到整个基于IP的网络的连通性。由于IP协议没有方向,甚至它都没有会话的概念,因此路由必然要是双向的,否则数据就有去无回了(有人提倡用NAT来解决反向路由问题,实际上NAT在公共核心网络上口碑十分不咋地,它甚至破坏了IP协议的原则,记住,NAT一般只用于端点)。互联网如此之大,每个路由器上的路由信息会非常之多,路由器是怎么在海量的路由信息中用最快的速度-显然很重要-检索出自己需要的呢?另外如此海量的路由信息又是怎么生成的呢?本文着重回答第一个问题,关于第二个问题请参考《Internet路由结构(第二版)》(Cisco Press,想看就赶快买,不买就买不到了,Cisco有几本书真的很火爆,总是不好买)
1.基本概念
路由的概念:路由是一种指向标,因为网络是一跳一跳往前推进的,因此在每一跳都要有一系列的指向标。实际上不仅仅是分组交换网需要路由,电路交换网在创建虚电路的时候也需要路由,更实际的例子,我们日常生活中,路由无处不在。简单的说,路由由三元素组成:目标地址,掩码,下一跳。注意,路由项中其实没有输出端口-它是链路层概念,Linux操作系统将路由表和转发表混为一谈,而实际上它们应该是分开的(分开的好处之一使得MPLS更容易实现)。路由项通过两种途径加入内核, 一种是通过用户态路由协议进程或者用户静态配置配置加入,另一种是主机自动发现的路由。所谓自动发现的路由实际上是“发现了一个路由项和一个转发表”,其含义在主机某一个网卡启动的时候生效,比如eth0启动,那么系统生成下列路由表项/转发项:往eth0同一IP网段的包通过eth0发出。
路由表:路由表包含了一系列的表项,包括上述的三元素。
路由框架的层次:路由大致分为两个要素,也可以看成两个层次。第一个层次是路由表项的生成;第二个层次是主机对路由表项的查找。
路由表项生成算法:生成路由表项的方式有两种,第一种是管理员手工配置,第二种为通过路由协议动态生成。
路由查找算法:本文着重于主机层面上对路由表项的查询算法。毕竟这是一个纯技术活儿... 相反的,路由协议的实现和配置更讲究人为的策略,如果你人为配置RIP或者OSPF只需要配几条命令就OK了,那么配一个BGP试试,它讲究大量的策略,不是纯技术能解决的。如果有时间,我会单独写一篇文章谈路由协议的,但是今天,只谈路由器/主机对路由表项的查找过程。
这个过程很重要,如果路由器的查找算法效率提高了,那么很显然,端到端的延迟就降低了,这是一定的。
2.Linux的哈希查找算法
这是Linux操作系统的经典的路由查找算法,直到现在还是默认的路由查找算法。然而它很简单。由于它的简单性,内核(kernel)开发组一直很推崇它,虽然它有这样那样的局限性,但由于Linux内核的哲学就是“够用即可”,因为Linux几乎从来不被用于专业的核心网络路由系统,因此哈希查找法一直都是默认的选择。2.1.查找过程
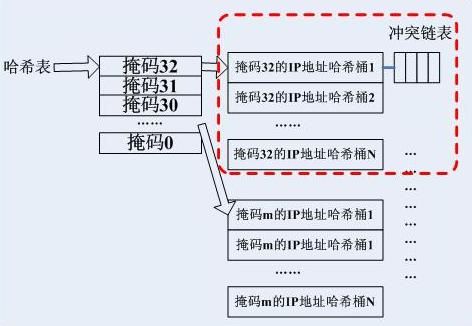
查找结构如下图所示:
查找顺序如下图所示:
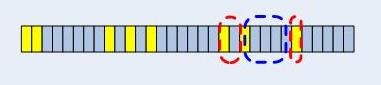
为了实现最长前缀匹配,从最长的掩码开始匹配,每一个掩码都有一个哈希表,目的IP地址哈希到这些哈希表的特定的桶中,然后遍历其冲突链表得到最终结果。
注意,哈希查找算法是基于掩码的遍历来实现严格的最长前缀匹配的,也就是说如果一条最终将要通过默认网关发出的数据报,它起码要匹配32次才能得到结果。 这种方式十分类似于传统的Netfilter的filter表的过滤方式-一个一个尝试匹配,而不像HiPac的过滤方式,是基于查找的。接下来我们会看到,高性能的路由器在查找路由的时候使用的都是基于查找型数据结构的方式,最常用的就是查找树了。2.2.局限性
我们知道, 哈希算法的可扩展性一直都是一个问题,一个特定的哈希函数只适合一定数量的匹配项,几乎很难找到一个通用的哈希函数,能够适应从几个匹配项到几千万个匹配项的情形,一般而言,随着匹配项的增加,哈希碰撞也会随着增加,并且其时间复杂性不可控,这是一个很大的问题,这个问题阻止了哈希路由查找算法走向核心专用路由器,限制了Linux路由的规模,它根本不可能使用哈希来应对大型互联网络或者BGP之类的域间路由协议产生的大量路由信息。核心路由器上,使用哈希算法无疑是不妥的,必定需要找到一种算法,使得其查找的时间复杂度限制在一个范围( 我们不关心空间复杂度,这和端到端用户的体验没有关系,只和他们花的钱多少有关,花10万买的路由器有4G内存,花100万买的路由器则支持64G内存...)。我们知道,基于树的查找算法可以做到这一点,实际上,很多的路由器都是使用基于树的查找算法来实现的。我们先从Linux的trie树开始。便于查阅代码(虽然本文不分析代码...)。
3.Linux的LC-Trie树查找算法
trie算法分为三大块,第一块是查找,第二块是插入/删除,第三块是平衡。我们首先先不管其名称为何这么叫,也不必非要去深入理解一下Trie树的概念,直接实践就是了。虽然很多的教科书都喜欢最后讲查找型数据结构的插入,而我这里却要先说插入,因为一旦你明白了插入,查找就不言自明了,另外,讲完插入之后,接下来我要说的是trie树的平衡以及多路操作,因为这样的话,最终的查找才会变得高效。我们权当高效的查找操作是一个必然结果吧。3.1.基本理论
很不好意思,这里没什么理论,一切都很简单。我们可以通过电话号码来认识trie树,trie树本质上是一棵检索树,和全球电话号码簿一样,我们知道,电话号码有三部分组成:国家码+地区号+号码,比如086+372+5912345,如果从美国拨出这个号码,首先要决定送往哪个国家,所要做的就是用确定位数的国家码和出口交换机的转发表的国家码部分进行匹配,发现086正好是中国,然后该号码到达中国后,再匹配区号,发现要送往安阳市,最后到达安阳市,然后将请求发往5912345这个号码。现在的问题是,在每一个环节如何使用最快的方式检索到请求下一步要发往哪里?我想最好的方式就是使用 “桶算法”,举个例子,在美国的电话请求出口处放置一张表,表项有X个,其中X代表全球所有国家和地区的总和,中国的国家码是086,那么它就是第86个表项,这样直接取第86个表项,得到相应的交换信息,电话请求通过信息中指示的链路发往中国...
另外一个例子就是计算机的页表,这个我们在3.3节再谈。
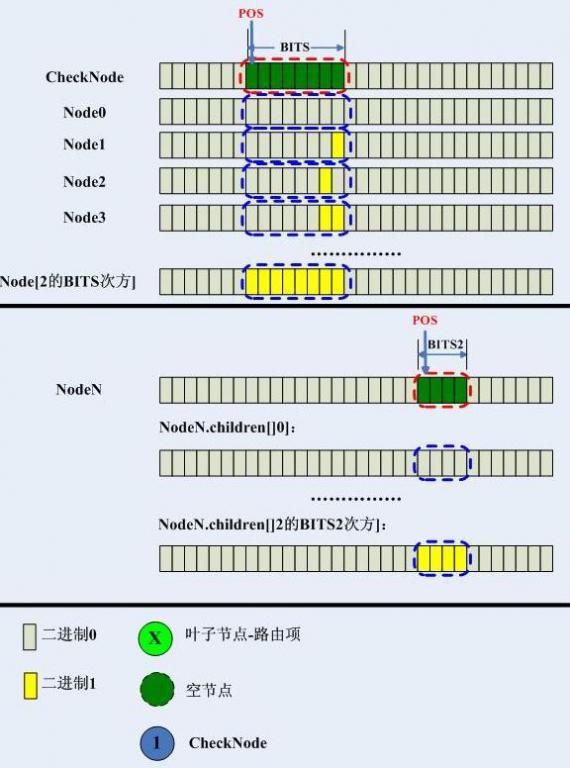
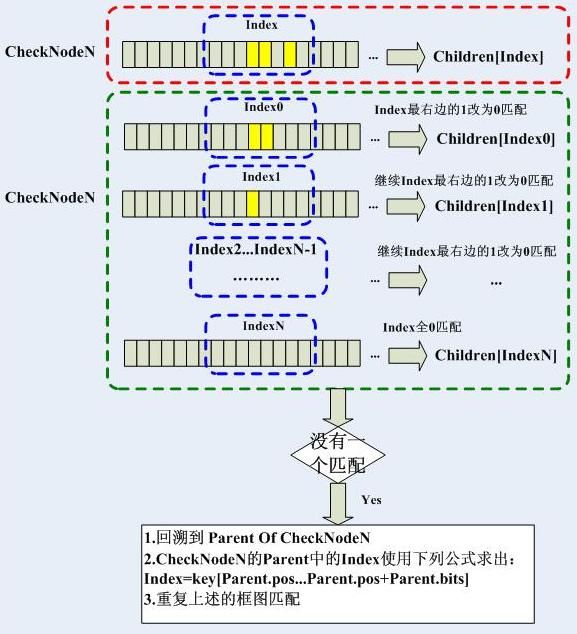
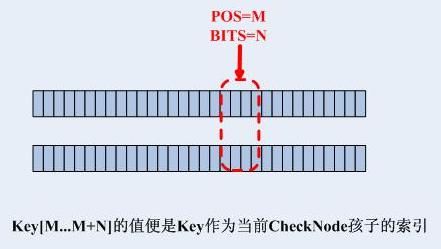
trie树,其实和上述的结构差不多,只不过上述结构的检索分段是固定的,比如电话号码就是3位10进制数字等,且匹配检测索引的位置也是固定的,比如电话号码的地区号就是从第4位十进制数字开始等。对于trie树而言,需要检测的位置不是固定的,它用pos表示,而检测索引的长度也不固定,它由bits表示,我们把每一个检测点定为一个CheckNode,它的结构体如下:
CheckNode{
int pos;
int bits;
Node children[1<<bits];
}
union Node{
Leaf entry;
CheckNode node;
}
图解如下:
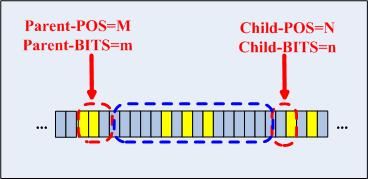
可见pos和bits是一个CheckNode的核心,pos指示从哪一位开始检测,bits指示了孩子结点数组,直接取key[pos...pos+bits]即可直接取到孩子结点。
3.2.trie树的插入
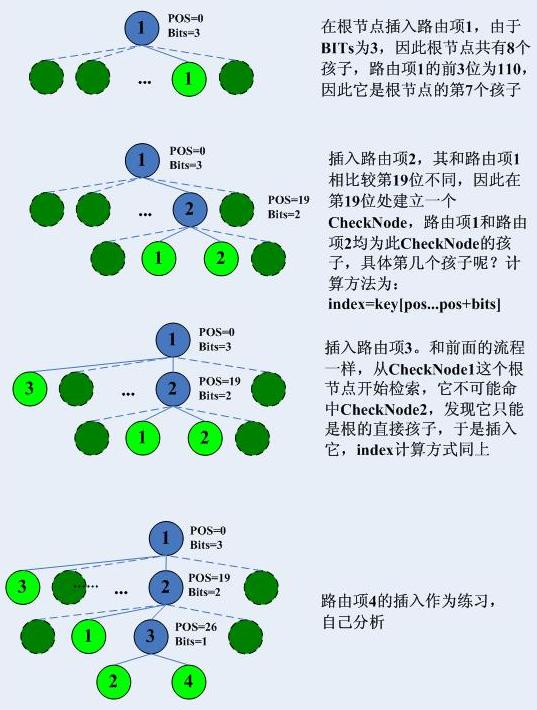
我以为,研究一种树型结构的时候,首先理解其插入算法无疑是最好的,然而很多的教科书都是从检索开始,然后将插入操作一笔带过,这是很不妥的。我认为只要把插入操作理解深刻了,接下来的查询和删除就很简单了,毕竟插入是第一步!插入虽然重要,但是想学习的人不要认为它很难,要知道,只要是人想出的东西,理解它们都不会很难,难的是什么?难的是你不会首先想不出来!插入应该怎么进行呢?:第一步,如果一个CheckNode节点都没有,则创建根CheckNode节点,并且创建一个叶子,结束。注意,每一个路由项都是一片叶子。如果已经有了根CheckNode,则需要计算新节点插入的位置。
第二步,计算插入位置前的位置匹配。步骤如下:
根据已有CheckNode的pos/bits信息,从根开始执行一系列比较:
1).取出根CheckNode
2).设当前CheckNode为PreCheckNode
3).判断是否需要继续匹配。
4).如果需要继续匹配,则看看自己是其哪个孩子或者该孩子的分支,并且取出该孩子Child-CheckNode为当前CheckNode,回到2。
5).如果不需要继续匹配,退出匹配过程
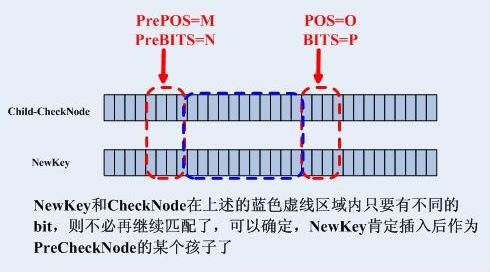
其中判断CheckNode是否需要继续匹配其Child-CheckNode的算法如下:
NewKey和CheckNode在上述的蓝色虚线区域内只要有不同的bit,则不必再和Child-CheckNode继续匹配了,可以确定,NewKey肯定插入后作为PreCheckNode的某个孩子了。如果需要继续匹配,判断是哪个孩子的方式如下:
第三步,确定插入位置并且插入,步骤如下:
0).如果没有发生第二步中的和Child-CheckNode不匹配的情形,则直接将NewKey作为叶子作为PreCheckNode的第NewKey[PreCheckNode的pos...PreCheckNode的pos+PreCheckNode的bits]插入,结束。否则执行下面的步骤,处理和Child-CheckNode的冲突1).创建一个CheckNode,然后看下图:
假设上图中的绿色圈起来的位是Child-CheckNode和NewKey首次不匹配的地方,记为miss,那么NewKey将创建一个新的CheckNode,记为NewNode,其POS为miss,其bits为1,这样原来的Child-CheckNode就成了NewNode的一个孩子,而待插入的NewKey创建一个新的叶子,作为NewNode的另一个孩子。NewNode代替Child-CheckNode作为PreCheckNode的孩子插入其孩子数组中。
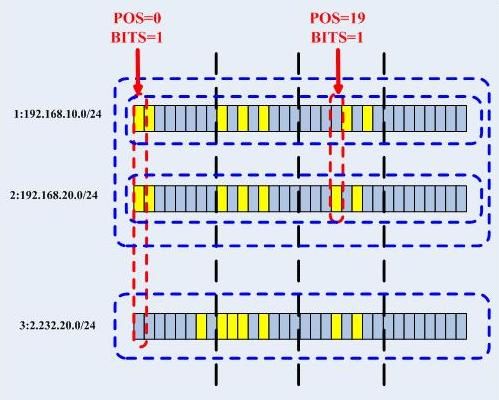
第四步,完毕基本上,上述的过程已经很清楚了,然而给出一个例子会更好些,接下来我给出一个例子,依次插入3条路由项:
1:192.168.10.0/24
2:192.168.20.0/24
3:2.232.20.0/24
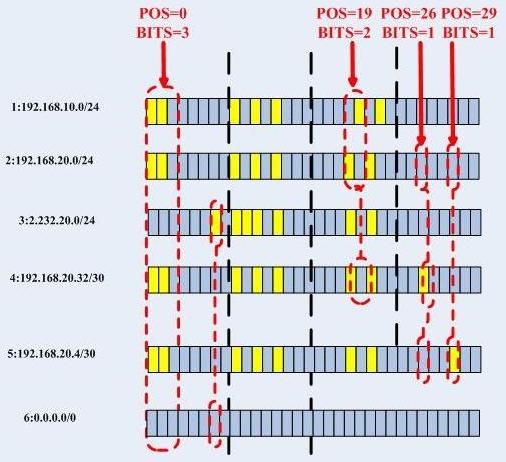
然后我们看图说话,首先看一下比特图:
接下来看一下插入trie的情形:
3.3.trie平衡以及多路trie
如果仅仅看3.2节所论述的内容,我们发现trie 不过是一棵二叉查找树而已,这又有何好说的呢?然而作为路由表结构的trie却远不止这么简单。如果我们现在还想不到作为路由表的trie树长什么样子,我们可以先考虑一下页表,毕竟这是实现虚拟内存的关键,处理器设计者一定会选择一种相当高效的方式来从虚拟地址查找物理地址的,页表使用分段索引的方式来快速定位页表项,也就是说将一个虚拟地址分为N段,每一段定位一个索引,然而将这些索引层接起来就是最终的页表项。这里就不再给出图示了,关于页表的资料很多。如果把页表结构从页目录展开来看的话,页表结构就是一棵大分叉的树,足有4096叉,然而却不高,也就两层到四层。我们想一下它为何如此高效,因为它比较矮小,索引可以快速定位树的分支,最终快速到达叶子。
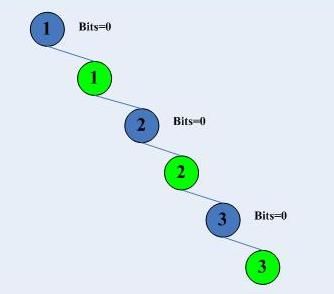
但是,且慢,树矮小的代价是什么?时间复杂度小了,空间复杂度一般都会变大。它太耗内存了。因此最好的方案就是,树不能太高,也不能太矮。多路的trie树就是这样设计的。极端情况下,多路trie树会退化成一个链表或者进化成一棵“2的32次方”叉的只有两层的树:
链表情形-bits=0
多叉树情形-bits=32
而动态多路trie所要维护的就是让这棵树不这么极端。
我们首先看一眼普通多路trie树的插入情形,注意,所谓多路trie树插入是假的,在Linux的实现中,只有平衡操作才能让trie成为多路的,这里给出的实例在Linux中是不会出现的,只有经过平衡操作的trie树才会是这个样子,也就是说,不可能一插入就是这样的,具体的CheckNode的bits在这里是事先确定好的,而在Linux的实现中却是动态调整的。多路trie的本质在于其“多路”,而多路的本质在于CheckNode的bits字段。看一下上面讲查入时的例子,此时我们又多了一个路由项从而多了一个节点,首先看比特图:
再看一下多路trie树:
这就是多路trie树。
所谓的平衡操作很简单,每次插入新的节点都会平衡这棵树,原则如下:1).如果太高了,那么就压胖它。
使该CheckNode的pos不变,bits加1,使得其孩子的容量增大一倍,然后依次将其孩子重新加入新的CheckNode,加入过程中递归执行平衡操作。
2).如果太胖了,那就拉高它。
使该CheckNode的pos不变,bits减1,使得其孩子的容量减少一倍,然后依次将其孩子重新加入新的CHeckNode,加入过程中递归执行平衡操作。
总之,Linux实现的trie树是动态变化的,这种动态变化的优点是可以根据系统当前的负载以及内存情况动态对trie树的形态做出调整,使得资源的总体利用率提高,然而也有缺点,那就是算法本身太复杂,不适合做扩展,最重要的是不适合用硬件实现。
3.4.trie树的查找
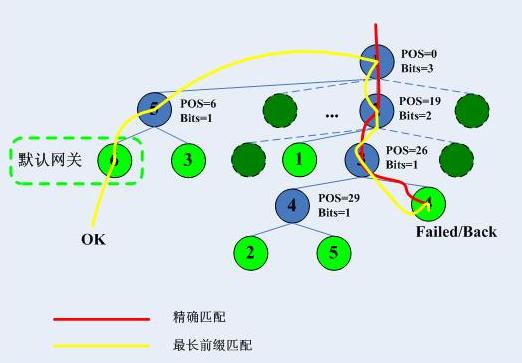
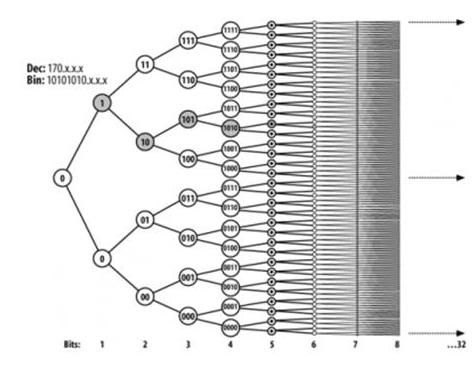
终于到查找操作了。在我们理解了上述的插入和平衡操作之后,查找就变得很简单了,我们不但可以看得出其简单-好的算法一般都简单,并且由于平衡操作算法还来得很高效,唯一的新东西就是回溯,不过这一节我们只介绍一般回溯,下一节介绍关于回溯的优化。查找其实非常简单,简单的让我都不想写算法流程了,我家小小又闹了,加上又喝点酒...来个例子吧,比如来了一个数据包,目的地址是192.168.10.23,来看一下怎么查找,将该地址写成二进制:
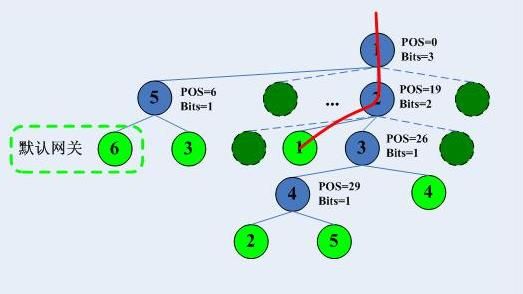
根据trie树根,得知pos=0/bits=3,因此知道应该去往根CheckNode的第7个孩子,于是到达CheckNode2,类似的,我们检查该ip地址的第19位后面的两位,到达叶子节点1,由于其掩码为24,通过,顺利找到,在描述树查找过程前,我先将添加默认网关的比特图给出:
然后给出trie树:
整个trie查找过程为,红线标示查找过程:
接下来我们看看回溯,首先看看为何要回溯。trie树不像页表,检测范围覆盖整个32位虚拟地址,trie的检查点覆盖范围之间会有空隙:
蓝色虚线圈住的区域就是空隙-(见路径压缩),万一在查找时,在这个区域发生不匹配,是不能直接检测出来的,这样好像查找过程就进入了一个死胡同,注意,第一次匹配查找的过程是精确匹配,这次进入了死胡同之后,马上转变查找策略,将从精确匹配转为“最长前缀匹配”,由于越靠近叶子的节点的前缀(理解为子网掩码)越长-因为它比较精确,所以这次查找采用从叶子到根的方式,查找最长前缀的匹配,这就是回溯,举例来讲:
1).111100和111110不匹配
2).但是它却和111000,110000,100000,000000都匹配
3).取最长的匹配,那就是111000
比如来了一个目的地址是192.169.20.32,按照上面的方式,将跳过第16位的不同,最终达到的叶子节点是4,然而最终的整体检查失败,进入最长前缀匹配,也就是回溯,首先回溯到哪呢?当然是CheckNode3,然后下一步呢?在介绍下一步之前,我们看看回溯的原则。最长前缀匹配中,0是很重要的,只要某个匹配项除了后面的0,前面都匹配,那就算成功匹配,我们需要做的是找到“最长”的匹配。哪个是最长的匹配呢?我们可以通过一个算法得到结果,这也是Linux内核中所使用的算法:
这样的结果,我们看一下整个过程:
最后,值得注意的是,每一个CheckNode和Leaf都有一个前缀链表,比如:
192.168.10.0/24 via 1.2.3.4
192.168.10.0/27 via 4.3.2.1
两个entry就共享一个Leaf,然而该Leaf却有两个掩码,两个掩码链接成链。当发生匹配的时候,必须依次匹配每一个链表上的掩码。有两个原则决定了最终的匹配结果的前缀是最长的,第一,从树根到叶子的精确匹配;第二,每个叶子节点的掩码链表是按照从长到短的顺序排列的。
3.5.回溯优化
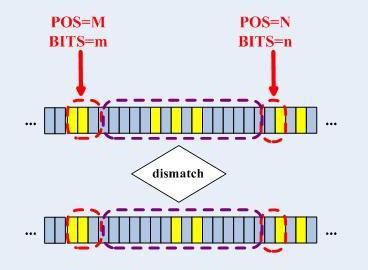
回溯是很低效的,比如上面的例子,整个绕了两圈,如果能提前发现那个不匹配的位,那就不用耗费那么多的无用功了,实际上做到这一点很简单,那就是在取下一个孩子的时候,判断一下:在当前CheckNode的[pos+bits]和欲往的孩子节点的[pos+bits]之间有不同的比特吗?如果有,看看CheckNode中不同的那位以后是否全0,如果是,则直接检测该CheckNode的掩码链表,否则直接回溯,这样就不必做无用功了。这种“忽略的不匹配”现象如下所示:
检查到了这种情况之后,匹配过程马上进入“最长前缀匹配”,将掩码从32位(精确匹配)减少到和当前CheckNode的key[pos+bits]个孩子的第一个不匹配的位指示的那个位置:
检索键和匹配项相差别的那一位,不是0就是1,只有在匹配项的那位是0(检索键的那位是1)的时候,检索才能继续下去,否则,回溯!继续检索之后,按照常规的匹配来匹配,区别就是掩码不同,精确匹配时是32位掩码匹配,而最长掩码匹配是N位掩码匹配。
3.6.动态多路trie树的本质-路径压缩
由于多路trie树的目的快速从根节点找到一个叶子节点,然后匹配,如果不匹配的话就回溯,因此表示路由表的trie树就应该能快速一条唯一的从根到叶子的路径,因此树的高度不便太高,因此没有必要对查找键每一个比特位都进行检测,trie树中的CheckNode中的pos以及bits决定了在哪个地方检测已经检测多少位,而trie树此时是已经建好的,可以把当前已插入路由项之外的比特信息检测全部忽略掉,这就是路径压缩,见下图:
检索键的蓝颜色圈起来的位在精确匹配过程中暂时不需要进行匹配,等到最长前缀匹配时再考虑。路径压缩的好处在于匹配时计算的次数会减少,然而随着更多的路由项的插入,很多的节点将会使下列的等式成立:
node.pos=Pnode.pos+Pnode.bits(Pnode为node的Parent)如果一个CheckNode有太多这样的孩子,说明进入此分支的匹配全部都要“走很长的路”了,那么为了使匹配操作“路途更短”,该进行一次平衡操作了,所要做的就是将高树压低压胖。
4.BSD/Cisco的Radix查找算法
4.1.基本理论
很多时候,还是这个名称造成了极大的困惑,radix树?基树?二叉树?...停吧!4.2.radix查找
复杂的多路trie树查找我们都已经会了,这个还难吗?可能唯一的区别就是BSD的树相对于Linux的而言比较固定,因此更易于用硬件来并行实现,华为的VRP因此也受益良多!举个例子来说明这一点,如果我们将IP地址分为相等的4个部分,每一部分就是8个位,那么就很容易将4个索引并行处理,即使不并行处理,使用硬件交叉网络来实现也是蛮快的,可以看到,这和页面的查询非常类似了,只是页表查找失败会引发缺页异常,而路由查找失败将回溯。还是那个问题,回溯到哪里?基本算法和trie树一样,也是依赖每一个CheckNode都存在一个掩码链表...5.BSD/Cisco的X叉树查找算法
5.1.基本理论和查找
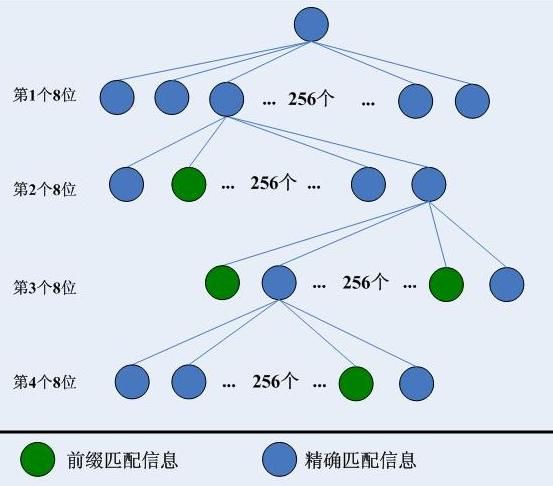
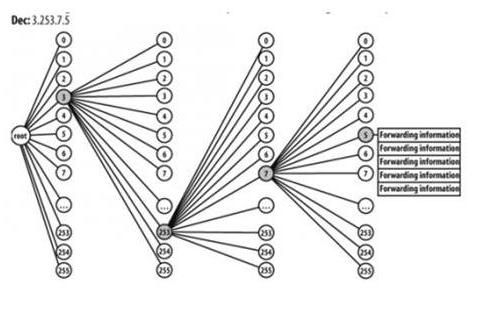
用空间换时间,这是一种不太疯狂且很正当的举动,因为时间相比空间要重要的多,人们对时间的敏感性也比对空间的敏感性更高,空间广义的说可以是无限的,而时间却存在一个个的阀值。另外,并行也是空间换时间的一个直接益处,我们知道并行是一个时间上的概念。Linux的trie树的回溯优化版本中,发现不匹配就回溯,回溯的过程中包含了一个一个尝试的步骤,无非就是从右到左依次将1变成0后再次尝试前缀匹配,这种方式固然可行,然而如果能直接指出下个匹配哪个节点,那就不需要回溯过程中的尝试行为了。而这正是Cisco的实现,传说中的256叉树就是用固定的4个8位一组来定位索引的,和页表项查找一样,一旦出现不匹配的或者索引对应的孩子为NULL的,直接根据节点结构中指示的“下一个节点”来直接到达下一个节点处继续匹配。比特结构见下图:
可见,这种256叉树中间没有空隙,也就是说每一个比特都要参与索引定位,不会有遗漏的,另外在插入的时候,已经动态计算好了节点不存在时将要从哪里继续开始匹配,也就是说每一个空节点都包含一个指针,指向“下一个可能匹配的节点”,另外在每一个非空节点中,也包含一个指针,指向“下一个可能匹配的节点”(这个指针几乎不用),因此回溯时不再需要动态计算,回溯只需要在得到“下一个可能匹配的节点”后,一路往下取全0的孩子即可,这就是“前缀匹配”。256叉树可以一步到位的进行查找,大大提升了效率。其查找树如下:
查找过程很简单,计算第一个8位为P,第二个8位为Q,第三个8位为L,第四个8位为N,因此匹配项在树中每层(从第2层开始)的索引为P,Q,L,N。这样很容易定位到最终的节点,如果是一个空间点,表示没有精确的匹配项,那么就开始回溯,回溯过程走上图中的红色线路。
因此一次查找操作在有限次数内就能找到,树很矮,时间效率很高,相当高,然而由于所有的路径都是在插入时确定的,因此其插入操作比较复杂,不过即使再复杂无非也就是和多路trie树查找时做的那样,计算一下回溯路径而已,然后将其添加到256叉树的节点项中,最终路由查找的时候高效的直接使用,仅此!
5.2.评价
256叉树的查找结构是一个一般性的路由表结构, 实际上Cisco路由器的CEF的实现是上述256叉树的某种优化-CEF使用的数据结构是一个256-way-mtrie,它本质上也是分为4层,和上述的没有什么两样,只是不再存在空节点,也没有了红色粗线表示的静态回溯路径,而是直接把那条红线最终指向的节点的信息直接写入到那个空节点中。看起来如下这个样子:
实际上CEF使用的也是一棵多路trie树,只不过这棵树比较容易和硬件建立关联,从而用硬件建立转发表,而Linux的trie是动态的,纯软件的。
6.总的评价
总的评价不谈哈希算法,因为哈希函数的可扩展性很差,我本身也不是很喜欢这个东西,虽然Linux内核中大量使用了哈希,但是正是这些哈希限制了Linux支持应用的规模,寻找好的哈希函数简直太难了,如果这会儿你的西墙倒了,并且你此时并不在乎东墙,那么你就用哈希吧,拆了东墙补西墙!树算法是不错的选择,确定性强,而且越是简单的树实际上效率越高,这是为什么呢?因为易于用硬件实现,专业级的硬件还是要比单纯使用cpu的软件效率高几个级别的。 是设计高效复杂的纯软件算法还是用硬件实现一个简单然而并不怎么高效的算法,这是一个问题。基本上可以确定,一般而言,纯硬件实现的遍历要比纯软件实现的哈希好很多,硬件是信号,电流驱动的,而软件依赖cpu指令,时钟周期等...
本文基本就介绍了路由查找使用的两种树,第一种是二叉树,如下图(图片来自google的结果):
第二种是256叉树,如下图(图片来自google的结果):